Sejam uma v.a. discreta e
a função de massa de probabilidade (f.m.p.) para
, então
-
para um subconjunto enumerável de pontos de
;
-
, em que a soma e sobre todo
tal que
;
- a função de distribuição acumulada (f.d.a) é
, em que a soma e sobre todo
tal que
;
-
.
A f.m.p. caracteriza a distribuição de probabilidades da variável aleatória.
O valor esperado de e a variância de
são dados, respectivamente, por
onde as somas são sobre todo tal que
.
— Distribuição de Bernoulli —
Na prática, ocorrem muitas situações com experimentos que admitem apenas dois resultados, por exemplo
- uma peça é classificada como boa ou defeituosa;
- o resultado de um exame médico é positivo ou negativo;
- um paciente submetido a um tratamento é curado ou não da doença;
- um entrevistado concorda ou não concorda com a afirmação feita;
- no lançamento de um dado ocorre ou não ocorre a face “5”.
Nessas situações podemos representar, genericamente, os resultados do experimento com o espaço amostral
e o modelo probabilístico fica determinado dado . Esses experimentos recebem o nome de Ensaios de Bernoulli e a v.a. indicadora do evento “sucesso” é uma variável aleatória de Bernoulli com parâmetro
.
A notação indica que
é uma v.a. com distribuição de Bernoulli de parâmetro
; ela assume dois valores
-
se ocorre sucesso,
-
se ocorre fracasso;
e sua f.m.p. é
e vale para outros valores de
.
A média e a variância de uma v.a. são dadas por
Exercício 59 Verifique as fórmulas acima para média e variância de uma v.a. de Bernoulli.
— Distribuição Binomial —
Consideremos repetições independentes de um Ensaio de Bernoulli. Seja
o número de sucessos nas repetições.
Exemplo 58 Um dado equilibrado é lançado 3 vezes. Qual é a probabilidade de se obter a face 5 duas vezes? Se
denota sucesso, i.e., “ocorre face 5” e
denota fracasso, “não ocorrer face 5” então podemos representar o espaço amostral por
e
e
. Como podemos determinar, por exemplo,
A função de massa de probabilidade é

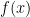


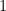

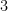
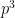
e podemos escrever essa função como
para todo
. Assim,
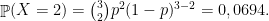
Uma variável aleatória com distribuição binomial de parâmetros e
é uma v.a. com f.m.p.
que pode ser vista como o número de sucessos em ensaios independentes de Bernoulli e com mesma probabilidade
de sucesso.
De fato, se são as v.a. indicadoras de sucesso em cada um dos ensaios, então
é a quantidade de sucessos ocorridos.
A notação indica que
é uma v.a. com distribuição binomial com parâmetros
e
. A média e a variância de
são dadas por
Essas duas igualdades podem ser deduzidas da identidade em que
. De fato, usando que
na segunda identidade abaixo
Exercício 60 Verifique as fórmulas para média e variância de uma v.a. binomial (use a identidade dada acima).
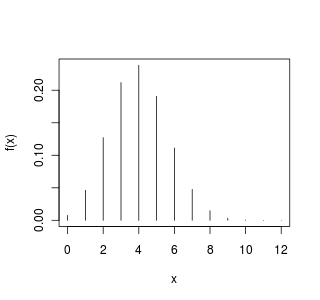
Exemplo 59 Numa prova com 12 questões de múltipla escolha, com 3 alternativas, se todas as respostas forem chute, então a função de massa de probabilidade
tem o seguinte gráfico de barras
A seguir, respectivamente, os gráficos mostram a distribuição nos casos de uma prova com 120 questões e 2 alternativas, uma prova com 120 questões e 3 alternativas e uma prova com 120 questões e 5 alternativas
o primeiro dos gráficos pode ser obtido com o R fazendo
x<-0:12 p=1/3 n=12 plot(x,dbinom(x,n,p),type="h")
A primeira linha diz os valores de pros quais queremos
. A segunda e terceira linhas atribuem os parâmetros da distribuição binomial, o parâmetro
é
e
é
. Podemos usar o único comando
plot(0:12,dbinom(0:12,12,1/3),type="h")
é para o tipo de gráfico com barras. Os outros 3 gráficos acima são dados, respectivamente, por
plot(0:120,dbinom(0:120,120,1/2),type="h") plot(0:120,dbinom(0:120,120,1/3),type="h") plot(0:120,dbinom(0:120,120,1/5),type="h")
Exemplo 60 Um equipamento resiste a um teste de choque com probabilidade
. Qual é probabilidade de que em
testes
equipamentos sobrevivam ao choque?
Exemplo 61 Uma febre atinge 25% dos rebanhos. Se
animais não ficam doente então
Os indivíduos de rebanhos de vários tamanhos recebem vacina.
população proporção de sadios análise 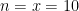

se nenhum animal ficar doente, pode ser que a vacina seja eficaz 
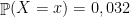
se nenhum animal ficar doente, pode ser que a vacina seja eficaz 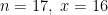
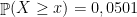
se ficar doente, evidência mais forte de eficácia que 0 doentes em 10
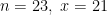
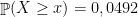
doentes em 23 é evidência mais forte que 1 em 17 e 0 em 10 de eficácia
Usando R:
Para , podemos calcular
em R usando
no exemplo acima, para cada linha, respectivamente, os valores são obtidos com
pbinom(10,10,.75) - pbinom(9,10,.75) pbinom(12,12,.75) - pbinom(11,12,.75) 1 - pbinom(15,17,.75) 1 - pbinom(20,23,.75)
A primeira linha da tabela também é obtida com
dbinom(10,10,.75)
e a segunda com
dbinom(12,12,.75)
.
Exemplo 62 Um fabricante garante que seu produto tem uma taxa de itens defeituosos de
.
Numa seleção de 20 itens a serem inspecionados, qual é a probabilidade de ao menos um ser defeituoso?
Se
é a quantidade de itens defeituosos
Se 10 carregamentos por mês deixam a fabrica e de cada carregamento 20 itens são inspecionados, com que probabilidade 3 carregamentos tem pelo menos um item defeituoso?
Seja . Para
e
fixos, quando
varia de
a
o valor de
cresce monotonicamente e depois decresce monotonicamente. De fato,
que é se e só se
ou, equivalentemente,
.
Proposição 12 Seja
. Para
e
fixos, quando
varia de
a
o valor de
cresce monotonicamente e depois decresce monotonicamente atingindo o máximo quando
.

Notemos que o ponto de máximo é aproximadamente o valor médio, o que sugere que os maiores valores de estão em torno da média (reveja os gráficos do exemplo 59).
Exemplo 63 Numa doença rara, um paciente se recupera com probabilidade
. Em 15 pacientes doentes, seja
o número de sobreviventes.
- pelo menos
sobrevivem.
- de
a
pacientes sobrevivam
. Usando a desigualdade de Chebyshev
portanto
com probabilidade
. A v.a.
tem média e variância dadas, respectivamente, por
e
, portanto com probabilidade
~
está no intervalo
.
Notemos que, no exemplo acima, não foi preciso usar os valores de e
para derivar o limitante
para a probabilidade. Isso se deve ao fato de Chebyshev valer pra qualquer distribuição e, por isso, a estimativa não é muito precisa.
Exemplo 64 Numa eleição, seja
a fração (desconhecida) da população que vota no candidato
. Para simplificar, assumimos que um voto em voto em
é ensaio de Bernoulli com parâmetro
.
Suponha que são realizadas
entrevistas:
é a v.a. indicadora do
-ésimo voto ser para
, para
. Então
é o total de entrevistados a favor de
. Ademais, a razão
é uma estimativa para
.
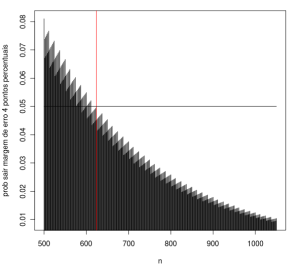
Queremos determinar
para obtermos uma estimativa para
com erro de 4 pontos percentuais com pelo menos 95% de certeza (grau de confiança). i.e.,
Usando a desigualdade de Chebyshev (17),
e fazendo o lado direito igual a
e resolvendo para
obtemos
entrevistas para que
estime
dentro dos parâmetros de exigência. Acontece, que Chebyshev é uma desigualdade fraca devido a sua generalidade com respeitos às v.a.’s, ela não usa nenhuma particularidade da distribuição binomial que, pela proposição anterior, parece estar bem concentrada em torno da média.
A eq. (26) equivale a
e a soma a esquerda da desigualdade é
que é máxima para
para todo
fixo, portanto
que é menor que
para
.
Usando R:n<-500:1000 plot(n,2*pbinom(.46*n,n,1/2),type="h")Essa estimativa é bem próxima a de dados reais. Informações obtidas no sítio do IBOPE referentes ao 1º turno das eleições municipais de 2008 exibem a seguinte quantidade de entrevistados de acordo como o erro e o grau de confiança:
— Distribuição de Poisson —
A notação indica que
é uma v.a. com distribuição de Poisson com parâmetro
, a qual assume valores no conjunto dos naturais com f.m.p. dada por
A média e a variância de é
Exercício 61 Use que
para provar que
. Prove que
. Conclua que
.
Ocasiões em que aparecem uma variável aleatória de Poisson são aquelas em que, geralmente, estamos interessados no número de eventos que ocorrem em um intervalo fixo de tempo (ou numa região de área fixa, ou de volume fixo) se esses eventos ocorrem com uma taxa média conhecida e independentemente do tempo desde a última ocorrência. Por exemplo,
- o número de erros de impressão numa página de livro;
- o número de chamadas que chega a uma central telefônica;
- o número de partículas
descarregadas por um material radioativo em um período fixo de tempo;
o que é justificado pelo seguinte. Suponha que em ensaios independentes de Bernoulli com probabilidade de sucesso
a taxa média de sucesso é
. A probabilidade de
sucessos é
, para
.
Para
portanto, para suficientemente grande
(pela definição de
como limite de uma sequência). Agora, usando (25) podemos concluir que
o que podemos estender usando indução para
que é conhecido como a aproximação de Poisson para a distribuição binomial; em resumo fixado e fixado
, se
e
, então
e uma prova pode ser vista aqui.
Exemplo 65 Um telefone recebe em média 5 chamadas por minuto. Supondo que a distribuição de Poisson seja um modelo adequado para essa situação, qual a probabilidade com que o telefone não receba chamadas durante um intervalo de 1 minuto?
Exemplo 66 O número de partículas que contaminam a superfície de um CD no processo de fabricação tem distribuição de Poisson. O número médio de partículas é

e a área de um CD é
. Seja
o número de partículas num CD;
.
dpois(12,10)
ou
ppois(12,10) - ppois(11,10)
para item 1
ppois(12,10)
para o item 3
plot(0:20,dpois(0:20,10),type="h")
para o gráfico?
Exemplo 67 Suponha que essas notas tenham erros tipográficos por página que segue uma distribuição de Poisson com
. Qual é a probabilidade de haver pelo menos um erro nessa página? Se
é a quantidade de erros por página
Exemplo 68 Um analisador conta um número médio de
partículas por milésimo de segundo. Com que probabilidade um dado milésimo de segundo o contador contará
partículas?
Usando a desigualdade de Chebyshev (17) a probabilidade do evento
, em que
é o número de partículas num determinado milésimo é
Exercício 62 Prove que a f.m.p. de
satisfaz
.
— Distribuição Hipergeométrica —
Uma v.a. com distribuição hipergeométrica com parâmetros tem f.m.p.
A média e a variância de uma v.a. hipergeométrica são dadas por
em que . A prova dessas fórmulas é similar à prova para v.a. binomial, segue da identidade
em que
é uma v.a. hipergeométrica com parâmetros
.
Exercício 63 Mostre as identidades
e obtenha delas a identidade
. Em seguida, deduza as igualdade para média e variância.
Uma coleção de objetos contém
Uma amostra com elementos é selecionada. Qual a probabilidade da amostra conter
(
) bolas azuis? O número de bolas azuis é uma v.a. hipergeométrica.
Exemplo 69 Qual a probabilidade de acertar 4 dos 6 números sorteados na mega-sena? Os parâmetros são
e
, logo
Exemplo 70 Um comprador de componentes elétricos compra os componentes em lote de 10. A política de controle de qualidade é inspecionar 3 componentes escolhidos aleatoriamente e comprar o lote somente se os 3 não apresentarem defeitos. Se 30% dos lotes têm 4 componentes com defeito e 70% apenas 1, qual é a proporção de lotes rejeitados? Consideremos os eventos:
“aceita um lote” e
“lote com 4 peças com defeito”.
Exemplo 71 Um produto é distribuído em lotes de 40 unidades. Um lote é inaceitável se três ou mais itens apresentam defeito. O departamento de controle de qualidade de um comprador adotou o plano de selecionar 5 itens e rejeitar o lote se um item inspecionado for defeituoso.
Num lote com 3 itens defeituosos, a probabilidade de haver um defeituoso numa amostra de 5 é
ou seja, detecta um lote ruim em apenas 30% dos casos. Como já vimos, se
é o número de itens defeituosos na amostra, então
com probabilidade pelo menos
, pela desigualdade de Chebyshev. Nesse caso
e
e temos então que menos que 2 itens em 5 são defeituosos com probabilidade
, ou seja, em 75% dos casos.
Exemplo 72 (Estimativa de máxima verossimilhança) Num lago 1000 peixes foram capturados, marcados e devolvidos. Uma nova captura de 1000 peixes é feita 100 deles estão marcados. O que pode ser dito a respeito do tamanho da população de peixes no lago?
A probabilidade do evento em função do número (desconhecido) de peixes desmarcados tem gráfico de barras
sugere uma população de aproximadamente 9.000 + 1.000 peixes (máxima verossimilhança — estimativa que maximiza a probabilidade do evento ocorrido, aqui essa estimativa por ser feita de modo análogo a (25)).
— Outras distribuições —
Uma v.a. com distribuição geométrica com parâmetro tem f.m.p. dada por
que correspondente ao número de ensaios de Bernoulli independentes com parâmetro até ocorrer um sucesso. A notação
indica que
é uma v.a. geométrica com parâmetro
. A média e a variância de
são
Uma v.a. binomial negativa com parâmetros e
tem f.m.p. dada por
que correspondente ao número de ensaios de Bernoulli independentes com parâmetro até ocorrer um total de
sucessos.
Exercício 64 Mostre que se
é v.a. binomial negativa com parâmetros
e
e
é v.a. binomial negativa com parâmetros
e
, então
Deduza daí a média e a variância de uma v.a. binomial negativa com parâmetros
e
.
Uma v.a. com distribuição zeta (ou Zipf) com parâmetro tem f.m.p. dada por
A constante é
A distribuição deve seu nome a função zeta de Riemann e deve-se a George K.~Zipf sua popularização.
Finalmente, se
assume valores
com a mesma probabilidade, a saber
.