bc1435 – Quick-Sort | Notas de aula

O quicksort foi inventado por C.A.R. Hoare em 1960 e é muito rápido em geral, mas é lento em algumas raras instâncias especiais. O algoritmo tem complexidade de ordem ${n\log n}$ em média e a ${n^2}$ no pior caso.

Vamos começar com a análise da seguinte versão.

Quick-Sort

Quicksort

  Dado um vetor  A de números inteiros 
  Devolve os elementos de A em ordem não decrescente.

1 se (|A|= 1) então devolva(A)
2 senão
3     seja x o primeiro elemento em A 
4     para cada (y diferente de x em A) 
5         se (y < x) então coloque y em  
6         senão se (y > x)coloque y em  
7               senão coloque y em  
8 ordene, recursivamente,   e  
9 devolva (,,)

O custo $T(A)$ para ordenar o vetor $A$ é o custo para a criação dos subvetores $A_1,~A_x,~A_2$ , que é proporcional ao número de comparações das linhas 6 e 7 do algoritmo, ou seja $\Theta(n)$ , mais o custo para ordenar os subvetores $A_1,~A_2$ , que é $T(|A_1|)+T(|A_2|)$ . Notemos que não há nenhuma garantia a respeito dos tamanhos dos subvetores, por isso começaremos analisando dois casos extremos: (1) ${ | A_1 | = 0}$ e ${|A_2| = |A|-1}$ e (2) ${ | A_1 | = | A_2 | = (| A | - 1 )/2}$ .

No primeiro caso,

$T(n) = T(0) + T(n-1) + g(n)$ para aluma $g(n) = \Theta (n)$

de modo que obtemos $T(n) = \Theta ( n^2)$ (verifique usando indução). Por outro lado, se ${ | A_1 | = | A_2 | = (| A | - 1 )/2}$ então

$\displaystyle T(n) = T \left( \lfloor (n-1)/2 \rfloor \right) + T \left( \lceil (n-1)/2 \rceil \right) + g(n)$

de modo que obtemos $T(n) = \Theta ( n\log_2(n))$ (verifique).

De fato, se pensamos na árvore de recursão do quicksort percebemos que para garantir tempo ${O(n\log n)}$ é suficiente garantir que as subsequências geradas no pivotamento (linhas 3–7) tenham sempre uma fração ${\alpha \leq 1/2}$ constante do tamanho da sequência que as origina; nesse caso o número de instruções executadas em cada nível da recursão é $O(n)$ , que é o custo do pivotamento em cada subvetor, e a árvore tem altura $O(\log n)$ , portanto, o custo final é $O(n\log n)$ . De fato, a recorrência para o número de intruções executadas é

$\displaystyle T(n){=} T(\lfloor{\alpha n}\rfloor) + T(\lfloor{(1-\alpha)n}\rfloor) + \Theta(n)$

que é uma função limitada assintoticamente superiomente por ${n\log_{1/(1-\alpha)} n}$ . Por exemplo, se ${A_1}$ sempre tem 10% do tamanho de ${A}$ então o tempo gasto pelo quicksort numa instância de tamanho ${n}$ é ${T(n) = T(0{,}1n)+T(0{,}9n)+\Theta(n)}$ cuja solução é assintoticamente limitada por ${n\log_{10/9} n}$ .

Exercício 1 Prove que $\displaystyle T(n){=} T(\lfloor{\alpha n}\rfloor) + T(\lfloor{(1-\alpha)n}\rfloor) + \Theta(n)$ é $O(n\log n)$ .

Abaixo ${A[i..f] \leq A[f+1]}$ significa que para todo ${j \in [i..f]}$ vale ${A[j] \leq A[f+1]}$ .

— Pivotamento —

O processamento feito nas linhas 3 até 7 é chamado de pivotamento e ${\mathbf{x}}$ é chamado de pivô. O problema do pivotamento é

Dado um vetor  de  inteiros com 
            
Devolve  e os elementos de   rearranjados 
de modo que

No final do pivotamento o pivô está na sua posição correta (a posição no vetor com os elementos já ordenados) os elementos de ${A_1}$ são todos menores ou iguais a ${x}$ e o de ${A_2}$ maiores ou iguais a ${x}$ .

Usamos ${A[i] \leftrightarrow A[j]}$ para denotar troca do conteúdo das posições do vetor e usamos // comentário // para comentários no pseudocógido (texto que não é instrução do algoritmo), e os comentários no algoritmo abaixo são proposições que são verdadeiras naquele momento da execução.

Partição

Partição (A,i,f)

   Dado um vetor  de inteiros, com 
                  
   Devolve  e uma permutação de  tal que 
                  

1 e <- i; d <- f+1; x<- A[e]
2 Repita {
3 //  // 
4    Repita d <- d-1 Até que (A[d] <= x) ////
5    Repita e <- e+1 Até que (A[e] >= x) //// 
6    Se ( e < d ) A[e] <-> A[d] 
7    Senão devolva(d) }

Na última rodada do laço da linha 2 pode terminar de duas maneiras: $e=d$ ou $e=d+1$ . De fato, na última rodada

$e < d$ e em $A[e+1..d-1]$ não ocorre $x$ ; nesse caso o conteúdo desse subvetor, $A[e+1..d-1]$ , é uma sequência de números $< x$ seguida de uma sequência de números $>x$ . Nessa condição a variável $d$ é decrementada até encontrar um elemento do vetor $<x$ e, em seguida, a variável $e$ é incrementada até encontrar um elemento do vetor $>x$ o qual está a direita de $d$ , isto é, $e=d+1$ ;
$e < d$ e em $A[e+1..d-1]$ ocorre um único $x$ ; nesse caso $d$ é decrementada até encontrar $x$ e, em seguida, $e$ é incrementada até que encontre $x$ , assim o laço termina com $e=d$ .

Se $n=f-i+1$ então, no pior caso, $e=d+1$ e o número total de vezes que as linhas 4 e 5 são executadas é $n+1$ : se $d\neq i$ todas as posições do vetor, exceto $i$ e $e,d$ foram comparadas 1 vez com $x$ nas linhas 4 e 5, as posições $e,d$ foram comparadas 2 vezes; se $d= i$ todas as posições do vetor, exceto $e$ foram comparadas 1 vez com $x$ nas linhas 4 e 5 e a posição $e$ foi comparada 2 vezes.

No pior caso são executadas $3$ as instruções iniciais da linha 1, a linha 2 é executada $n+1$ vezes, essas duas linhas contribuem com $n+4$ instuções. A linhas 4 e 5 são compostas por 3 instruções executadas num total de $n+1$ vezes, portanto, essas linhas contribuem com $3n+3$ instruções. A comparação da linha 6 é executada do máximo $n+1$ vezes e as trocas no máximo $n$ vezes, sendo que cada troca é composta por 3 instruções, a linha 7 é executada 1 vez, portanto, são $4n+1$ instruções.

Teorema 1 O número de instruções executadas no pior caso pelo Partição para um vetor com $n$ itens é $8n+8$ .

Exercício 2 Mostre que durante toda a execução do algoritmo acima as propriedades nos cometários (entre // //) valem no momento em que o fluxo de instrução passa por elas.

Exercício 3 Prove que ao final da execução do algoritmo de pivotamento vale que $i\leq d < f$ .

— Quicksort —

O algoritmo de ordenação está descrito a seguir, nele assumimos que cada instância tem dois sentinelas nos seus extremos ${A[0] = -\infty}$ e ${A[n+1] = \infty}$ .

QuickSort (A,i,f)

QuickSort (A,i,f)

Dado um vetor  de inteiros.
Devolve  com seus elementos ordenados.

1 Se ( i < f )  
2 { q <- Partição (A,i,f) 
3   Quicksort (A,i,q-1)
4   Quicksort (A,q+1,f)
  }

Para ordenar o vetor $A[1..n]$ a chamada inicial se dá como Quicksort(A,1,n).

Exercício 4 Submeta um vetor crescente com ${n}$ itens ao Quicksort. Mostre que o algoritmo consome tempo proporcional a ${n^2}$ .

— Análise de pior caso —

Vimos acima que o número de instruções para Partição com uma entrada $A$ de tamanho $n$ é no máximo $8(n+1)$ em que $n+1$ é o número máximo de comparações feitas entre elementos do vetor $A$ . No que segue usaremos o número de comparações efetuadas entre elementos da entrada como parâmetro para estimar o custo do Quicksort.

A complexidade de tempo de pior caso é proporcional ao número de comparações entre elementos de ${A}$ executadas que, no pior caso, é

$\displaystyle T(n) = \max_{q\in [1..n-1]}\big( T(q-1) + T(n-q)\big) + n+1. \ \ \ \ \ (1)$

Lembremos que se supormos o caso da árvore de recursão longa então temos uma árvore de altura aproximadamente ${n}$ em que cada nível são executados aproximadamente ${n}$ instruções, portanto, a complexidade de pior caso é ${\Theta (n)}$ . Alternativamente, iterando a recorrência (1) vemos ${T(n) = (n+1) + n + (n-1) + \cdots + 3+2+1}$ , pois podemos assumir ${T(1)=1}$ , ou seja, ${T(n) =\Theta(n^2)}$ .

Vamos provar usando indução que ${T(n) \leq c n^2}$ para alguma constante positiva ${c}$ e todo ${n}$ suficientemente grande. Tomamos $c=1$ e $n_0=2$ .

Temos ${T(2)=4}$ , ${T(2) \leq c 2^2}$ . Assumamos, para a hipótese da indução, que ${T(k) \leq c k^2}$ para todo ${k\in [2..n-1]}$ , $n> 2$ . Dessa forma, para $c=1$ e todo $n \geq 2$

$\displaystyle \begin{array}{rcl} T(n) &=& \max_{q\in [1..n-1]}\big( T(q-1) + T(n-q)\big) + n+1 \\ &\leq & \max_{q\in [1..n-1]}\big( c(q-1)^2 + c(n-q)^2\big) + n+1 \\ &\leq & c(n-1)^2 + n+1 \\ &\leq & cn^2 -(2c-1)n +c+1 \\ &\leq & cn^2 . \end{array}$

Portanto, o Quicksort tem complexidade de pior caso ${O(n^2)}$ . Pelo exercício 4, para todo ${n}$ há uma instância com complexidade ${\Omega (n^2)}$ , logo o pior caso é ${\Theta (n^2)}$ .

Teorema 2 O número de instruções executadas no pior caso pelo Quicksort para ordenar um vetor com $n$ itens é $\Theta (n^2)$ .

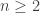
Exercício 5 Verifique que para todo $n\geq 2$ $\displaystyle \max_{q\in [1..n-1]}\big( c(q-1)^2 + c(n-q)^2\big) = c0^2 + c(n-1)^2$ .

— Análise de caso médio —

Para análise do caso médio assumiremos que as entradas de tamanho ${n}$ são todas as permutações de ${\{1,2,\dots,n\}}$ , assim na primeira etapa qualquer um dos ${n}$ elementos é o pivô com probabilidade ${1/n}$ , e assim sucessivamente nas próximas etapas, de modo que para ${n>1}$

$\displaystyle \begin{array}{rcl} M(n) &=& \displaystyle\frac 1n \sum_{q=1}^n \big( M(q-1) + M(n-q) \big) + n+1 \\ &=& \displaystyle\frac 2n \sum_{q=1}^{n-1} M(q) + n+1. \end{array}$

Pra resolver essa recorrência consideramos para todo ${n\geq2}$

$\displaystyle \begin{array}{rcl} n\cdot M(n) &=& \displaystyle 2 \sum_{q=1}^{n-1} M(q) + n(n+1) \\ (n-1)\cdot M(n-1) &=& \displaystyle 2 \sum_{q=1}^{n-2} M(q) + (n-1)n \end{array}$

subtraindo a segunda da primeira temos

$\displaystyle n\cdot M(n) - (n-1)\cdot M(n-1) = 2M(n-1) + 2n$

que é equivalente a

$\displaystyle n\cdot M(n) = (n+1)M(n-1) + 2n$

dividindo ambos os lados por ${n(n+1)}$

$\displaystyle \frac{M(n)}{n+1} = \frac{M(n-1)}n + \frac 2{n+1} \ \ \ \ \ (2)$

agora, se para todo ${n}$

$\displaystyle D(n) := \frac{M(n)}{n+1} \ \ \ \ \ (3)$

então

$\displaystyle D(n-1) = \frac{M(n-1)}{n}$

e reescrevemos (2) como

$\displaystyle D(n) = D(n-1) + \frac 2{n+1}$

que itera como

$\displaystyle \begin{array}{rcl} D(n) &=& D(n-1) + \frac 2{n+1}\\ &=& D(n-2) + \frac 2{n}+ \frac 2{n+1}\\ &=& D(n-3) + \frac 2{n-1}+ \frac 2{n}+ \frac 2{n+1}\\ &\vdots& \cdots \\ &=& D(2)+ \frac 24 +\cdots + \frac 2{n-1}+ \frac 2{n}+ \frac 2{n+1}\\ &=& \Theta(1)+ 2\left( \frac 14 +\cdots + \frac 1{n-1}+ \frac 1{n}+ \frac 1{n+1}\right) \end{array}$

Deixaremos como exercício mostrar que ${D(n) = \Theta (\log n)}$ . Assumindo esse fato temos, por (3)

$\displaystyle M(n) = \Theta(n \log n).$

Um defeito dessa análise é que ela não revela a distribuição de ${M(n)}$ , ou seja, embora a média seja ${\Theta(n \log n)}$ não sabemos dizer o quando o comportamento típico desvia da média. Para dar um exemplo simplificado desse fato, uma loteria que com probabilidade ${1/1000}$ dá um prêmio de ${1.000.000{,}00}$ e com probabilidade ${999/1000}$ dá um prêmio de ${1{,}00}$ tem ganho médio de aproximadamente ${1.000{,}00}$ mas um prêmio típico é de ${1{,}00}$ .

— Quicksort probabilístico —

Quicksort probabilístico

  Dado um vetor de números  
  Devolve os elementos de  ordem crescente.

1 se () devolva()
2 senão 
3     seja  um elemento escolhido ao acaso em  
4     para cada , ,
5          se () então coloque  em  
6          senão se () coloque  em  
7                senão coloque  em  
8 ordene, recursivamente,  e  
9 devolva ().

O pivotamento de ${S}$ nas linhas 3, 4, 5 e 6 do algoritmo acima, é considerado um sucesso se ${\min\{|S_{1}|,|S_{2}|\}\geq ({1/10})|S|}$ , caso contrário, dizemos que o particionamento foi um fracasso. Não há nada de especial na escolha de ${{1/10}}$ . Discutimos acima que se uma proporção for mantida no particionamento, digamos que a menor parte tem uma fração ${\alpha}$ da entrada, então a recorrência ${t(n)\leq t(\lfloor{\alpha n}\rfloor) + t(\lfloor{(1-\alpha)n}\rfloor) + cn}$ para constantes ${\alpha,c>0}$ tem solução ${O(n\log n)}$ .

Assim, cada particionamento é um experimento de Bernoulli com parametro ${p}$ . Um sucesso ocorre se ${x\in_{\mathrm{R}} S}$ não é um elemento dentre os 10% maiores elementos de ${S}$ nem um dos elementos dentre os 10% menores, ou seja, 80% dos elementos de ${S}$ são boos escolhas para ${x}$ , portanto, a probabilidade de sucesso é de ${{4/5}}$ .

Exercício 6 Mostre que um elemento da entrada participa de no máximo ${\lfloor{\log_{ {10}/{9}} n}\rfloor}$ particionamentos com sucesso.

Consideremos uma execução do quicksort com entrada ${S=x_1,x_2,\dots,x_n}$ . Seja ${X_{i}}$ o número de comparações entre o elemento ${x_i}$ da entrada e algum pivô durante toda uma execução do algoritmo. Em cada particionamento ${x_i}$ é comparado uma única vez (com o pivô); notemos que se ${x_{i}}$ é escolhido pivô então ele nunca mais participará de um particionamento e nunca mais será comparado com outro elemento de ${S}$ . Assim, o número total de comparações durante toda execução é ${X=\sum_{i=1}^{n}X_{i}}$ .

Fixemos ${i\in\{1,2,\dots,n\}}$ . Se ${Y_{k}}$ é o número de particionamentos ocorridos entre o ${k}$ -ésimo particionamento com sucesso (exclusive) do qual ${x_i}$ participa e o próximo particionamento com sucesso (inclusive) do qual ${x_{i}}$ participa, então

$\displaystyle Y_{k}\sim \mathrm{Ge}(p)$

em que ${p = 4/5}$ , logo ${\mathop{\mathbb E} Y_{k} < 2}$ . Ainda, pelo exercício 2 um elemento da entrada participa de no máximo ${\lfloor{\log_{10/9} n}\rfloor}$ particionamentos com sucesso, logo

$\displaystyle X_{i} = \sum_{k= 1}^{\rfloor{\log_{\frac {10}9} n}\lfloor}Y_{k}.$

Pela linearidade da esperança

$\displaystyle \mathop{\mathbb E} X_{i} < 2\lfloor{\log_{\frac {10}9} n}\rfloor ~\quad \textrm{e} ~\quad \mathop{\mathbb E} X < 2n \lfloor{\log_{\frac {10}9} n}\rfloor \ \ \ \ \ (4)$

Com isso, provamos o seguinte.

Lema 1 O número esperado de comparações numa execução do quicksort aleatorizado sobre uma entrada com ${n}$ elementos é ${O(n\log n)}$ .

É sabido, da Análise de Algoritmos [CLR] que todo algoritmo de ordenação baseado em comparação faz no mínimo da ordem de ${n\log n}$ comparações para ordenar ${n}$ elementos, ou seja, em média o quicksort aleatorizado é o melhor possível. Porém, saber que um algoritmo é bom em média, não nos garante que ele é bom quase-sempre. Vamos mostrar que com alta probabilidade o desempenho do algoritmo está próximo da média, isto é, para quase-toda instância o número de comparações está próximo da média (e bem longe do pior caso). Vamos provar o seguinte resultado.

Teorema 3 O número de comparações numa execução do quicksort aleatorizado com uma entrada de tamanho ${n}$ é ${O(n\log n)}$ com probabilidade

$\displaystyle 1 - O(n^{-6}).$

Demonstração: Definimos

$\displaystyle L = \lceil{8 \log_{\frac {10}9} n}\rceil$

e consideramos o evento ${X_{i} > L}$ , ou seja, segundo (4) ${x_{i}}$ foi comparado mais do que quatro vezes o valor esperado para o número de comparações realizadas pelo algoritmo entre ${x_i}$ e os pivôs. Teremos ${X_{i} > L }$ se em ${ L }$ particionamentos ocorrem menos que ${ \lfloor{ \log_{10/9} n}\rfloor}$ sucessos, ou seja, o número de fracassos em ${L}$ particionamentos é pelo menos

$\displaystyle \lceil{8 \log_{\frac {10}9} n}\rceil - \lfloor{ \log_{\frac {10}9} n}\rfloor > {8 \log_{\frac {10}9} n}- \log_{\frac {10}9} n = 7\log_{\frac {10}9} n.$

Seja ${Z_i}$ o número de particionamentos com fracasso pelos quais ${x_{i}}$ passa em ${L}$ particionamentos. Então, ${Z_i \sim \mathrm{Bi} \big( L,1-p\big)}$ com ${p = 4/5}$ . Vamos estimar a probabilidade do evento ${Z_i > 7 \log_{10/9} n}$ , com isso, teremos uma estimativa para a probabilidade de ${X_{i} > L}$ . A probabilidade de ocorrerem ${j}$ fracassos em ${L}$ experimentos é ${\binom{L}{j} \left( 1-p \right)^{j} p^{L -j}}$ , portanto,

$\displaystyle \begin{array}{rcl} \mathop{\mathbb P}\left(Z_i \geq 7\log_{\frac {10}9} n\right) &\leq& \displaystyle \sum_{j\geq \lceil{7 \log_{\frac {10}9} n}\rceil}\binom{L}{j} \left( 1-p \right)^{j} p^{L -j}\\ &\leq& \displaystyle \sum_{j\geq\lceil{7 \log_{\frac {10}9} n}\rceil}\binom{L}{j} \left( \frac 15 \right)^{j} \\ & \leq&\displaystyle \sum_{j\geq\lceil{7 \log_{\frac {10}9} n}\rceil} \left( \frac{\mathrm{e}L}{5j} \right)^{j} \\ &\leq& \displaystyle \sum_{j\geq\lceil{7 \log_{\frac {10}9} n}\rceil} \left( \frac{\mathrm{e}L }{5\lceil{7\log_{\frac {10}9} n}\rceil} \right)^{j} \end{array}$

mas

$\displaystyle \frac{\mathrm{e}\lceil{8\log_{\frac {10}9} n}\rceil}{5\lceil{7\log_{\frac {10}9} n}\rceil} < \frac 25 \cdot \frac{9\log_{\frac {10}9} n}{{8\log_{\frac {10}9} n}} < \frac 9{10}$

assim,

$\displaystyle \begin{array}{rcl} \displaystyle \sum_{j\geq\lceil{7 \log_{\frac {10}9} n}\rceil} \left( \frac{\mathrm{e}\lceil{8\log_{\frac {10}9} n}\rceil}{5\lceil{7\log_{\frac {10}9} n}\rceil} \right)^{j} \leq \sum_{j\geq\lceil{7 \log_{\frac {10}9} n}\rceil} \left( \frac 9{10} \right)^{j} = O(n^{-7}). \end{array}$

Portanto, a probabilidade de existir ${i}$ com ${X_{i} > \lceil{8 \log_{\frac {10}9} n}\rceil}$ é

$\displaystyle \mathop{\mathbb P}\left(\bigcup_{i=1}^{n} \left[ X_{i} > \lceil{8 \log_{\frac {10}9} n}\rceil \right]\right) = O(n^{-6}),$

logo, com probabilidade ${1 - O( n^{- 6} )}$ vale que ${ X_{i} \leq 8 \log_{ {10}/9} n}$ para todo ${i}$ e que, com essa probabilidade, quicksort aleatorizado executa ${\leq 8n\log_{ {10}/9} n}$ comparações entre elementos da entrada. $\Box$

Notas de aula

Jair Donadelli

bc1435 – Quick-Sort

Deixe um comentário Cancelar resposta

Compartilhe isso:

Relacionado

Deixe um comentário Cancelar resposta