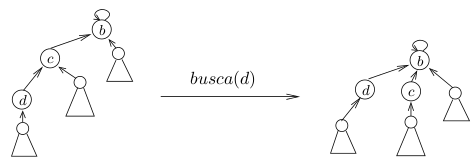bc1435 – União e busca

O problema é representar dinamicamente uma família ${\mathcal{C}=\{C_1,C_2,\dots,C_k\}}$ de subconjuntos disjuntos de um universo ${\mathcal U}$ de modo que cada conjunto é identificado por um representante que é um elemento do próprio conjunto e que não tem nenhuma outra propriedade especial, o importante é que, dado que o conjunto não mudou, toda vez que se pergunta pelo representante a resposta deve ser a mesma. Para as nossas aplicações podemos assumir, sem perda de generalidade, que ${\mathcal{U}=\{1,2,\dots,n\}}$ .

Essas estruturas devem comportar as operações ${cria}$ , ${busca}$ e ${uni\tilde ao}$ sobre ${\mathcal{C}}$ :

${{cria}(x)}$ cria o conjunto unitário ${C_{k+1}=\{x\}}$ em ${\mathcal C}$

${{busca}(x)}$ devolve o representante do conjunto ao qual ${x}$ pertence;

${{uni\tilde ao}(x,y)}$ substitui em ${\mathcal{C}}$ os conjuntos que contém ${x}$ e ${y}$ pela união desses dois conjuntos; se ${x\in C_x}$ e ${y\in C_y}$ então ${{uni\tilde ao}(x,y)}$ remove os conjuntos ${C_x}$ e ${C_y}$ de ${\mathcal{C}}$ e acrescenta ${C_x\cup C_y}$ a ${\mathcal{C}}$ , além disso escolhe-se um representante para ${C_x\cup C_y}$ .

Queremos uma representação que seja eficiente, ou seja, o objetivo é a análise da complexidade das operações em algumas estruturas de dados. Para tal, suporemos que serão executadas $m$ operações $uni\tilde ao$ e $busca$ em uma ordem não conhecida a partir da criação de $n$ conjuntos unitários, o que chamamos de configuração inicial.

Representação usando vetor

Usamos um vetor ${C}$ indexado por ${\mathcal U}$ e a idéia é que dois elementos do conjunto universo ${x}$ e ${y}$ estão no mesmo conjunto se e somente se as posições ${x}$ e ${y}$ do vetor têm o mesmo conteúdo, assim ${C_k = \{x\in \mathcal{U}\colon C[x]=k\}}$ . Escolhemos como representante do conjunto o menor elemento. Dessa forma, os algoritmos para as operações ${cria}$ , ${busca}$ e ${uni\tilde ao}$ ficam da seguinte forma

cria(x)
   C[x] ← x.

busca(x)
   devolva(C[x]).

união(x,y)
   k ← min{busca(x),busca(y)};
   Para Cada i de 1 até n
      Se ( C[i]=C[x] ou C[i]=C[y] )  C[i]← k;

Claramente, cada união tem custo $O(n)$ .

Teorema 1 A complexidade de ${m}$ operações num universo com ${n}$ elementos é ${O(mn)}$ . ${\Box}$

Observamos que a complexidade de pior caso não está superestimada como mostra a seguinte sequência de $m=n-1$ operações depois de: ${cria(1)}$ , ${cria(2) \dots cria(n)}$ que estabelece a configuração inicial

$\displaystyle \begin{array}{rcl} uniao(2,1)\\ uniao(3,2)\\ uniao(4,3)\\ uniao(5,4)\\ \vdots\\ uniao(n,n-1) \end{array}$

Representação usando listas ligadas

Cada conjunto é dado por uma lista ligada. A cada elemento do universo está associado um nó com os atributos ${prox}$ que aponta para o próximo elemento da lista e ${rep}$ que aponta para o representante do conjunto.

Por exemplo, se por ora consideramos o universo ${\{a,b,c,d,e,f,g,h,i\}}$ , então um esquema da representação dos subconjuntos ${\{c,d,e\}}$ , ${\{a\}}$ e ${\{b,f,g,h\}}$ é dada na figura:

As funções ${cria}$ e ${busca}$ operam ligeiramente diferente da que vimos:

${{cria}(x)}$ cria um novo nó apontado por ${x}$ ;

${{busca}(x)}$ devolve um ponteiro para o representante do único conjunto ao qual ${x}$ pertence;

${{uni\tilde ao}(x,y)}$ une os conjuntos que contém ${x}$ e ${y}$ concatenando-se as listas e atualizando-se os ponteiros ${rep}$ de todos elementos de uma das listas.

Um ${busca(x)}$ é feito em tempo constante e o custo de ${uni\tilde ao(x,y)}$ é basicamente o custo das atualizações dos ponteiros. Dessa forma, a complexidade de tempo das operações nessa representação é da mesma ordem de grandeza da representação por vetor. A mesma sequência de $m=n-1$ operações após ${cria(1)}$ , ${cria(2) \dots cria(n)}$ ,

$\displaystyle \begin{array}{rcl} uniao(2,1)\\ uniao(3,2) \\ uniao(4,3)\\ uniao(5,4)\\ \vdots\\ uniao(n,n-1) \end{array}$

em que $uniao(i+1,i)$ atualiza $i$ ponteiros dos elementos do conjunto do $i$ e, portanto,
resulta em $\sum_{i=1}^{n-1} i = O (n^2) =O(mn)$ operações.

Adotando a seguinte heurística, a complexidade melhora substancialmente:

${(\ddag)}$ Atualizar sempre a menor lista: pressupondo um atributo ${\ell[C]}$ que armazena o número de elementos de ${C}$ , numa união de duas listas concatenamos a menor lista no final da maior lista.

Para um elemento ${x}$ do universo, a primeira vez que ${{rep[x]}}$ é atualizado resulta numa lista de tamanho pelo menos ${2}$ . A segunda vez que ${{rep[x]}}$ é atualizado resulta numa lista de tamanho pelo menos ${4}$ e assim por diante. Logo, o número de atualizações que ${rep}$ [ ] de um elemento qualquer é atualizado é no máximo ${\log_2 n}$ .

Proposição 2 Supondo a heurística ${(\ddag)}$ se o representante de ${x}$ muda ${k}$ vezes, então o tamanho da lista que contém ${x}$ é pelo menos ${2^k}$ .

Demonstração: A prova é por indução em ${k\in{\mathbb N}}$ que vale: se o representante de ${x}$ muda ${k}$ vezes, então o tamanho da lista que contém ${x}$ é pelo menos ${2^k}$ , para qualquer elemento ${x}$ do universo. Para ${k=0}$ , ${x}$ é o único elemento na lista dele e portanto temos a base da indução. Para ${k\geq 1}$ assumimos que se ${k-1}$ atualizações foram feitas então a lista de ${x}$ tem tamanho pelo menos ${2^{k-1}}$ . Na próxima atualização do representante de ${x}$ ocorre numa união com uma lista que tem pelo menos o mesmo número de elementos da lista de ${x}$ , resultando numa lista com pelo menos ${2\cdot 2^{k-1}=2^k}$ elementos. O resultado segue do Princípio da Indução Finita. $\Box$

Após uma sequência de $m$ uniões, a partir da configuração inicial, o maior conjunto tem no máximo $m$ elementos, portanto o representante de um elemento $x$ pode ter mudado no máximo ${ \lfloor \log_2(m)\rfloor}$ vezes.

Corolário 3 O representante de um elemento qualquer do universo muda no máximo ${ \lfloor \log_2(n)\rfloor}$ vezes. ${\Box}$

Dessa forma o custo total para atualização dos ponteiros dos $n$ objetos é no máximo $O(n\log_2 n)$ .

Teorema 4 O tempo para ${m}$ operações num universo com ${n}$ elementos é ${O(m+n\log n)}$ . $\Box$

— Representação por floresta —

A idéia é que cada subconjunto seja representado por uma árvore de modo que cada elemento do subconjunto seja representado por um nó da árvore. Nessa árvore cada nó não-raiz aponta para um pai e a raiz é o representante; o pai da raiz é ela mesma (e só raiz tem essa propriedade). Dessa forma, ${cria}$ cria em tempo constante uma nova árvore que contém somente a raiz, ${uni\tilde ao}$ é feita em tempo constante mudando-se o pai de uma das raízes e ${busca}$ , que tem tempo dependente da profundidade do elemento na árvore, retorna um ponteiro para uma raiz.

Uma representação com árvores dos subconjuntos ${\{c,d,e\}}$ , ${\{a\}}$ e ${\{b,f,g,h\}}$ e o resultado de ${uni\tilde ao (e,f)}$ .

Desa forma $uni\tilde ao$ agora é barato enquanto que $busca$ é caro, tem custo da ordem da altura da árvore. Claramente, essa estrutura pode ser muito ruim se a árvore formada for uma lista linear entretanto, com algumas heurísticas bastante simples o resultado final melhora substancialmente. Começamos com a seguinte heurística para união de dois subconjuntos, onde tamanho de uma árvore é o número de nós

União por tamanho: árvore de menor tamanho é colocada como sub-árvore da árvore de maior tamanho.

Definimos a altura de uma árvore como a maior distância (número de ponteiros percorridos) de um nó até a raiz e temos a seguinte relação entre tamanho e altura resultantes de uma sequência de uniões com a heurística de união por tamanho.

Lema 6 Num universo com $n$ elementos e usando união por tamanho, após uma sequência qualquer de uniões a partir da configuração inicial vale que o número de nós de cada árvore é pelo menos ${2^h}$ , onde ${h}$ é a altura da árvore.

Demonstração: Vamos denotar por ${t(x)}$ o número de nós na árvore que contém ${x}$ e por ${h(x)}$ a altura da árvore que contém ${x}$ . Vamos provar o lema por indução no número de uniões: para todo ${k\in{\mathbb N}}$ , após ${k}$ uniões ${t(x)\geq 2^{h(x)}}$ para todo ${x}$ .

Com ${0}$ uniões estamos na configuração inicial, ou seja, ${t(x)=1}$ e ${h(x)=0}$ para todo ${x}$ , ou seja, a base da indução é verdadeira. Para ${k\geq 1}$ , vamos assumir que após ${k-1}$ uniões temos ${t(x)\geq 2^ {h(x)}}$ , para todo ${x}$ . Se a ${k}$ -ésima união é ${{uni\tilde ao}(x,y)}$ então ${t(z)\geq 2^{h(z)}}$ para todo ${z}$ com ${busca(z)\not\in\{ busca(x),busca(y)\}}$ , ou seja, a relação entre tamanho e altura não muda para as árvores que não estão envolvidas na união. Vamos denotar por ${t'}$ e ${h'}$ o tamanho e a altura da árvore resultante da união e ${t(x)}$ , ${t(y)}$ , ${h(x)}$ e ${h(y)}$ os tamanhos e as alturas antes da ${k}$ -ésima união.

Se $h(x)=h(y)$ então $h' = h(x)+1 = h(y)+1$ . Agora, $t' = t(x) + t(y)$ portanto $t' \geq 2^{h(x)}+2^{h(y)} = 2^{h(x)+1} = 2^{h'}$ .

Podemos assumir, sem perda de generalidade, que ${h(x)> h(y)}$ e dessa forma ${h'= h(x)+1}$ ou ${h'= h(x)}$ . A demonstração segue em dois casos:
${(i)}$ se ${h'=h(x)}$ então ${t'=t(x)+t(y)\geq t(x)}$ e pela hipótese de indução ${t(x)\geq 2^{h(x)}}$ , logo ${t'\geq 2^{h'}}$ ;
${(ii)}$ se ${h'=h(x)+1}$ então ${t'=t(x)+t(y)\geq 2\min\{t(x),t(y)\}\geq 2t(x)}$ (por quê?) e pela hipótese de indução ${t(y)\geq 2^{h(y)}}$ , logo ${t'\geq 2\cdot 2^{h(y)}=2^{h'}}$ .

Em ambos os casos temos que após ${k}$ uniões ${t(x)\geq 2^{h(x)}}$ para todo ${x}$ . A proposição segue pelo Princípio da Indução Finita. $\Box$

Corolário 7 O tempo de ${m}$ operações num universo de tamanho ${n}$ é ${O(m\log n)}$ .

Demonstração: Cada ${uni\tilde ao}$ toma tempo ${O(1)}$ , resultando em ${O(m)}$ . Cada ${busca}$ é feito em tempo ${O(\log n)}$ resultando em ${O(m\log n)}$ . $\Box$

Assumimos que cada nó ${x}$ tem um atributo ${t[x]}$ que armazena o número de elementos na árvore enraizada em ${x}$ os algoritmos ficam da seguinte forma

cria(x)
   pai[x] ← x;
   t[x] ← 1.

busca(x)
   enquanto ( x não é pai[x] ) x ← pai[x];
   devolva(pai[x]).

link(x,y)
    t[x]   ← t[x]+t[y];
    pai[y] ← x.

uniao(x,y)
    Se ( t[busca(x)] ≥  t[busca(y)] )
       link (busca(x),busca(y));
    Senão  link(busca(y),busca(x)).

Como o tempo das operações ${busca}$ são proporcionais a altura parece ser mais natural uma heurística que leva em conta a altura e não o tamanho da árvore.

União por altura: usamos a altura, ao invés do tamanho pendurando a árvore mais baixa na raiz da árvore mais alta.

Com essa heurística o Lema 6 continua valendo, e consequentemente o corolário. Os algoritmos para ${cria}$ , ${busca}$ e ${uni\tilde ao}$ são os algoritmos ${cria}$ , ${busca}$ e ${uni\tilde ao}$ com ${t}$ trocado por ${h}$ , que é iniciado com ${0}$ . Em ${link}$ só precisamos atualizar ${h}$ se as árvore envolvidas na união têm a mesma altura,

cria(x)
    pai[x] ← x.
    h[x] ← 0

link(x,y)
    Se ( h[x]=h[y] )  h[x] ← h[x]+1;
    pai[y] ← x.

Busca com compressão de caminhos e união por rank: quando fazemos um ${{busca}(x)}$ aproveitamos o percurso de ${x}$ até a raiz da árvore e desviamos os ponteiros ${{pai}[y]}$ , de todo ${y}$ nesse caminho, para a raiz; na união penduramos a árvore de menor rank na raiz da de maior rank.

Exemplo 1 Esquema de uma busca com compressão de caminhos.

Notemos que se estivermos usando união por altura, a compressão de caminhos modifica a altura da árvore e a atualização custa muito caro, portanto não a atualizamos e usamos ${{h}}$ como uma estimativa superior para a altura, que chamaremos de rank.

cria(x)
    pai[x] ← x.
    RANK[x] ← 0


busca(x)
   Se ( x não é pai[x] )  pai[x] ← busca(pai[x]);
   devolva(pai[x]).


link(x,y)
   Se ( RANK[x] = RANK[y] )  RANK[y] = RANK[y] + 1
   pai[x] ← y
   

uniao(x,y)
    rx 	← busca(x);
    ry 	← busca(y);
    Se ( RANK[rx] ≤  RANK[ry] ) link (rx,ry);
    Senão  link(ry,rx).

Essa duas heurísticas juntas, a união por rank e a compressão de caminhos é bastante eficiente. O próximo resultado, sobre a complexidade de ${m}$ operações num universo de tamanho ${n}$ , envolve uma função ${\alpha(m,n)}$ que cresce muito vagarosamente; na prática podemos assumir que ${\alpha=4}$ .

Teorema 8 (Tarjan, 1975) O tempo gasto com ${m}$ operações num universo de tamanho ${n}$ é ${O(m\alpha(m,n))}$ . ${\Box}$

Não demonstraremos esse teorema, o resultado que mostraremos a seguir é um pouco menos preciso.

Observação A função ${\alpha(m,n)}$ é uma função que cresce muito vagarosamente.

É, num certo sentido, a inversa da função de Ackermann ligeiramente modificada, dada por
$\displaystyle A(m,k)= \begin{cases} 2k & \textrm{ se } m=0,\\ 2 & \textrm{ se } m\geq 1 \textrm{ e } k=1,\\ A(m-1,A(m,k-1)) & \textrm{ caso contr\'ario}, \end{cases}$
conhecida por crescer muito rapidamente.

Por exemplo $A(1,j)= 2^j$ , $A(2,1)= 2$ , $A(2,2)= 2^{A(2,1)}= 4$ , $A(2,j)= 2^{A(2,j-1)} = 2^{2^{2^{\hdots^2}}}$ com $j$ ocorrências de $2$ . Ainda $A(3,4) = A(2,A(3,3))=A(2,A(3,3)) = A(2,A(2,A(3,2))) = A(2,A(2,A(2,A(3,1))))= A(2,A(2,A(2,2)))= A(2,A(2,4))= A(2,2^{2^{2^{2}}})=A(2,65536).$

${A(4,1)\sim 10^{80}}$ (maior que o número estimado de átomos no universo observável), e

$\displaystyle \alpha(m,n)=\min\big\{i\geq 1 \colon A(i,4\lceil{m/n}\rceil) > \log_2(n)\big \}.$

Para efeitos práticos podemos assumir ${\alpha < 5}$ .
Por exemplo

${n}$ ${\alpha(n,n)}$

${0}$ — ${2}$ ${0}$

${3}$ ${1}$

${4}$ — ${7}$ ${2}$

${8}$ — ${2047}$ ${3}$

${2048}$ — A(4,1) ${4}$

Denotamos por ${\log_2^* (n)}$ o número de vezes que temos que iterar ${\log_2}$ até que o valor obtido seja menor ou igual a ${1}$ , por exemplo,
${\log_2^* 3 = 2}$
${\log_2^* 5 = \log_2^* 6 =\log_2^* 7 = \dots = \log_2^* 16 =3}$
${\log_2^* 17= \dots =\log_2^* 2^{16}=4}$
${\log_2^* (2^{16}+1)= \cdots = \log_2^* 2^{65536}= 5}$
notemos que $2^{65536} > 10^{19000}$ .

Começamos a análise com as seguintes propriedades de rank.

Proposição 9 Quando um nó deixa de ser raiz o seu rank não muda nas próximas operações.

Proposição 10 ${rank[x] < rank[pai[x]]}$ para todo $x$ que não é raiz.

Segue por indução no número de operações executadas a partir da configuração inicial que essa propriedade é invariante pelas operações de $uni\tilde ao$ e $busca$ .

Proposição 11 Se um elemento tem rank $k$ então o tamanho da subárvore enraizada nele é pelo menos ${2^k}$ .

A prova é similar ao do Lema 6, por indução. Se $k=0$ então o elemento é raiz da árvore que contém pelo menos ele proóprio. Se ${x}$ tem rank $k$ ( $k>1$ ) então em algum momento teve rank $k-1$ e foi raiz de uma árvore que foi unida a outra de rank $k-1$ , portanto da união resulta uma árvore com pelo menos $2\cdot 2^{k-1}$ elementos.

Agora, particionamos os elementos de ${\mathcal{U}}$ em $\log_2^* n$ partes de acordo com o rank final do nó associado: o Grupo ${0}$ tem os elementos de rank ${0}$ e ${1}$ ; o Grupo ${1}$ tem os elementos de rank ${2}$ ; o Grupo ${2}$ tem os elementos de rank ${3,~4}$ ; o Grupo ${3}$ tem os elementos de rank ${5 \dots 16}$ ; o Grupo ${4}$ tem os elementos de rank ${17 \dots 2^{16}}$ ; o Grupo ${5}$ tem os elementos de rank ${2^{16}+1 \dots 2^{65536}}$ ; de um modo geral para ${k>2}$ o Grupo ${k}$ tem os elementos de rank em ${(k, 2^k ]}$ com $k = 2^{2^{\cdot^{\cdot^{\cdot^{2}}}}}$ .

Proposição 12 A quantia de nós cujo rank está no intervalo ${(k,2^k]}$ é no máximo ${n/2^k}$ .

De fato, pela Proposição 11, não pode haver mais que $n/2^r$ elementos de rank $r$ , portanto o número de elementos no intervalo mencionado é no máximo

$\displaystyle \sum_{r=k+1}^{2^k} \frac n{2^r}= \frac{n}{2^k}\sum_{i=1}^{2^k-k} \frac 1{2^i} < \frac{n}{2^k}\sum_{i=1}^{\infty} \frac 1{2^i} = \frac{n}{2^k}.$

Num busca(x) os apontadores no caminho de ${x}$ até a raiz serão redirecionados para a raiz. O custo da operação busca(x) é porporcional ao número de ponteiros percorridos de $x$ até a raiz. Classificamos esses apontadores $x \to y$ ( $y=pai[x]$ ) em 2 tipos:

Tipo 1 são os apontadores $x \to y$ com $x$ e $y$ em grupos diferentes ou ${y}$ é raiz, e
Tipo 2 são os apontadores $x \to y$ com $x$ e $y$ no mesmo grupo.

O número de ponteiros Tipo 1 que cada operação $busca$ percorre é no máximo $\log_2^* n$ , uma vez que existem apenas $\log_2^* n$ grupos e, pela Proposição 10, o percurso incrementa o rank. Portanto esses contribuem com

$\displaystyle O( m\log_2^* n).$

Para os ponteiros do Tipo 2, o ponto é que cada vez que uma operação $busca$ passa pelo elemento $x$ então $pai[x]$ passará a aopontar para a raiz da árvore corrente, portanto o rank de $pai[x]$ aumenta de pelo menos $1.$ Se $x$ está no grupo $(k,2^k]$ então $rank(pai[x])$ pode ser incrementado menos que $2^k$ vezes antes que $x\to pai[x]$ passe para o Tipo 1. Esses contribuem com