bc1405 – Números Naturais

Os axiomas de Peano apareceram na publicação de 1889 Arithmetic principia:
novo methodo exposita — Novo método de exposição dos princípios da Aritmética. Esses axiomas formalizavam a ideia de que todos os números naturais podem ser obtidos a partir do número 1 pela soma sucessiva da unidade. O grande mérito de Guiseppe Peano (1858-1932) foi a constatação de que a partir de quatro axiomas pode-se conceituar ou deduzir todas as definições e propriedades dos números naturais, como por exemplo: adição, multiplicação e relação de ordem. Na realidade, os axiomas conhecidos como Axiomas de Peano foram enunciados pela primeira vez por Dedekind um ano antes, em 1888. Dedekind usou de modo informal a teoria dos conjuntos, Peano, trabalhando de modo independente, não construiu sua teoria dentro da teoria dos conjuntos. Apresentamos a seguir uma breve exposição dos axiomas de Peano.

Axiomas de Peano-Dedekind. Vamos começar um estudo aritmético do conjunto ${{\mathbb N}}$ dos números naturais com uma abordagem formal a partir da construção lógica de ${{\mathbb N}}$ . Consideremos as noções elementares de conjunto e três conceitos primitivos: número natural, zero e sucessor de um número natural. O conjunto dos números naturais é caracterizado pelas seguintes propriedades:

Todo número natural possui um único sucessor, que também é um número natural.
Existe um número natural que não é sucessor de nenhum outro. Este número é chamado de zero e é representado pelo símbolo ${0}$ .
Números naturais diferentes possuem sucessores diferentes.
Axioma da Indução: Se um conjunto de números naturais contém o número ${0}$ e, além disso, contém o sucessor de cada um dos seus elementos, então esse conjunto coincide com o conjunto dos números naturais.

Ou seja, ${0\in {\mathbb N}}$ e existe uma função injetiva ${s\colon {\mathbb N} \rightarrow {\mathbb N}\setminus\{0\}}$ , que associa a cada ${n\in {\mathbb N}}$ um elemento ${s(n)\in {\mathbb N}}$ , chamado de sucessor de ${n}$ . O axioma da Indução fica escrito assim

Axioma da Indução: Para todo ${X}$ , se ${X \subset {\mathbb N}}$ é um subconjunto tal que

${0\in X}$ e
${\forall n,\; n\in X\Rightarrow s(n)\in X}$ ,

então ${X = {\mathbb N}}$ .

Exercício 3 Nenhum número é sucessor dele mesmo

Solução: Seja ${X}$ o conjunto dos números naturais ${n}$ tais que ${n\neq s(n)}$ .

${0\in X}$ pelo axioma 2.

${n\in X \Rightarrow n\neq s(n)}$ ; pelo axioma 3, ${s(n)\neq s(s(n))}$ , portanto, ${s(n)\in X}$ . Pelo axioma da indução ${X={\mathbb N}}$ . $\Box$

Exercício 4 Todo natural, exceto o zero, é sucessor de algum número natural.

Solução: Seja ${S}$ o conjunto de todos os naturais que são sucessores de outro natural. Definimos ${X:=\{0\} \cup S}$ . Então ${X \subset {\mathbb N}}$ e ${0\in X}$ .

Seja ${n\in X}$ , vamos mostrar que ${s(n) \in X}$ . Se ${n\neq 0}$ então ${n=s(m)}$ e ${s(n)=s(s(m))}$ (ax. 3); como o natural ${s(n)}$ é sucessor de alguém (a saber, de ${s(m)}$ ) ele está em ${S}$ , logo ${s(n) \in X}$ . Se ${n=0}$ , então ${s(0)\in S}$ , portanto, ${s(0)\in X}$ .

Pelo axioma da indução ${X={\mathbb N}}$ , portanto, ${S={\mathbb N}\setminus\{0\}}$ . $\Box$

Denota-se ${1:=s(0)}$ , ${2:=s(1)=s(s(0))}$ , ${3:=s(2)=s(s(s(0)))}$ e assim vai.

— Operações aritméticas —

Adição: Para cada ${m \in{\mathbb N}}$ , somar ${m}$ é definido por

${m+0=m}$ ;
${m+s(n)=s(m+n)}$ .

De modo que

$\displaystyle m+1= m+s(0)=s(m+0)=s(m). \ \ \ \ \ (9)$

Daí ${1+1=s(1)=2}$ . Notemos que ${s(1)=2}$ é uma definição enquanto que ${1+1=2}$ é um teorema.

Fixado ${m\in{\mathbb N}}$ , notemos que se

$\displaystyle X_m:=\{n\in{\mathbb N}\colon m+n \text{ est\'a definido }\}$

então pelo Axioma da Indução ${X_m={\mathbb N}}$ pois

${0\in X_m}$
se ${m+n}$ está definido então ${s(m+n) \in {\mathbb N}}$ logo ${m+s(n)}$ está definido.

${X_m={\mathbb N}}$ vale para todo natural ${m}$ , portanto, ${m+n}$ está definido para todo par de número naturais.

Observação:
${+}$ é uma operação binária ${+ \colon \mathbb{N} \times \mathbb{N} \to \mathbb{N}}$ e escrevemos ${a+b}$ para denotar ${+(a,b)}$ . É possíver provar que ${f\colon \mathbb{N} \to \mathbb{N}}$ que satisfaça ${f(0)=m}$ e ${f(s(n)) = s(f(n))}$ existe é única, ou seja, a soma é a única operação binária sobre ${\mathbb N}$ que satisfaz os itens 1 e 2 acima.

Multiplicação: Para ${m\in{\mathbb N}}$ , multiplicar por ${m}$ é definido por

${m\cdot 0 = 0}$
${m\cdot s(n) = m\cdot n+m}$ .

Exercício 5 Mostre que ${m\cdot n}$ está definido para todo par ${m}$ , ${n}$ de números naturais.

Observação:
${\cdot}$ é uma operação binária ${\cdot \colon \mathbb{N} \times \mathbb{N} \to \mathbb{N}}$ e escrevemos ${a\cdot b}$ para denotar ${\cdot (a,b)}$ . É possíver provar que ${f\colon \mathbb{N} \to \mathbb{N}}$ que satisfaça ${f(0)=m}$ e ${f(s(n)) = s(f(n))}$ existe é única, ou seja, a multiplicação é a única operação binária sobre ${\mathbb N}$ que satisfaz os itens 1 e 2 acima.

A adição e a multiplicação de números naturais têm as seguintes propriedades.

Teorema 1 Sejam ${a,b,c,m,n,p}$ números naturais quaisquer

(adição é associativa) ${(a+b)+c=a+(b+c)}$
Demonstração: Dados ${a}$ e ${b}$ , seja ${X:=\{c\colon (a+b)+c=a+(b+c)\}}$ . Se ${c=0}$ , então ${(a+b)+0=a+b}$ e ${a+(b+0) = a+b}$ , portanto ${0\in X}$ . Seja ${c\in X}$ . Então ${(a+b)+s(c)= s((a+b)+c) = s(a+(b+c))}$ . Usando a definição de soma duas vezes ${s(a+(b+c)) = a+s(b+c) = a+(b+s(c))}$ . Portanto ${s(c)\in X}$ . Pelo axioma da indução ${X={\mathbb N}}$ . $\Box$

(adição é comutativa) ${a+b=b+a}$
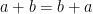
Demonstração: Começamos com o caso ${a=1}$ . Lembremos de (9) que ${s(b)= b+1}$ . Seja ${X=\{b\colon s(b)=1+b\}}$ . Verifique que ${0\in X}$ . Se ${b\in X}$ então ${s(b) = 1+b}$ , logo ${s(s(b)) = s(1+b) = 1+s(b)}$ , logo ${s(b)\in X}$ , portanto ${X={\mathbb N}}$ . Com isso ${b+1=1+b}$ para todo natural ${b}$ .

Agora, ${Y:=\{a \colon a+b=b+a (\forall b)\}}$ . ${0,1\in Y}$ . Se ${a\in Y}$ então ${s(a)+b = (a+1)+b = a+(1+b) = a+s(b) = s(a+b) = s(b+a)}$ . Agora, ${s(b+a) = b+s(a)}$ , portanto, ${s(a)\in X}$ . Assim ${Y={\mathbb N}}$ . $\Box$

(elemento neutro da adição) ${0}$ é o único natural tal que ${a+0=0+a=a}$
Demonstração: Que ${a+0=0+a}$ segue da comutatividade. Falta provar que ${0}$ é o único natural com essa propriedade. Seja ${u}$ tal que ${a+u=u+a=a}$ para todo natural ${a}$ . Tomando ${a=0}$ , ${u+0=0}$ portanto ${u=0}$ . $\Box$

(lei de cancelamento da adição) ${a+c=b+c \Rightarrow a=b}$
Demonstração: Exercício: dado que ${ a+s(c) = b+s(c) \Rightarrow s(a+c) = s(b+c) \Rightarrow a+c=b+c }$ justifique a última implicação e complete a demonstração. $\Box$

Se ${a+b=0}$ então ${a=b=0}$ .
Demonstração: Se ${a+b=0}$ e ${b\neq 0}$ então existe um natural ${c}$ tal que ${b=s(c)}$ e ${a+s(c)=0}$ . Da definição de soma ${s(a+c)=0}$ , que contradiz o axioma 2. Analogamente, se ${a\neq 0}$ então derivamos uma contradição. Portanto, ${a=b=0}$ . $\Box$

(elemento neutro da multiplicação) ${m\cdot 1 =1\cdot m = m}$ e ${1}$ é único com essa propriedade.
Demonstração: Exercício. $\Box$

(multiplicação é associativa) ${(m\cdot n)\cdot p=m\cdot (n\cdot p)}$ .
Demonstração: Exercício. $\Box$

(multiplicação é comutativa) ${m\cdot n = n\cdot m}$ .
Demonstração: Veja exercício 8 a seguir. $\Box$

(lei de cancelamento da multiplicação) ${mp=np \text{ e }p\neq 0 \Rightarrow m=n}$ .
Demonstração: Exercício. $\Box$

(multiplicação é distributiva com respeito a adição) ${(a+b)\cdot m = a\cdot m +b\cdot m }$ .
Demonstração: Exercício. $\Box$

Se ${m\cdot n = 0}$ então ${m=0 \text{ ou }n=0}$ .
Demonstração: Se ${m\cdot n = 0}$ e ${n\neq 0}$ . Então ${n=s(p)}$ para algum natural ${p}$ . Então ${m\cdot n = m\cdot s(p) = mp+m = 0}$ . Pelo item 5 ${mp=m=0}$ , assim ${m=0}$ . Analogamente, se ${m\neq 0}$ deduzimos que ${n=0}$ . $\Box$

Se ${m\cdot n=1}$ então ${m=n=1}$ .
Demonstração: Se ${m=0}$ ou ${n=0}$ então ${m\cdot n=0}$ pela definição de produto. Portanto, existem naturais ${a}$ e ${b}$ tais que ${m=s(a)}$ e ${n=s(b)}$ . Assim ${s(a)s(b) =1}$ , porém ${ 1 = s(a) s(b) = (a+1) (b+1) = ab +a +b +1}$ . Usando a lei de cancelamento da adição, item 4, ${ab+a+b=0}$ , portanto, ${ab = a+b = 0}$ . De ${a+b=0}$ temos ${a=b=0}$ , pelo item 5, logo ${m=n=1}$ . $\Box$

— Relação de ordem ${\leq}$ —

Para ${a,b\in{\mathbb N}}$ escrevemos

$\displaystyle a\leq b$

se existe um natural ${m}$ tal que

$\displaystyle a+m=b.$

Escrevemos ${a<b}$ caso ${m}$ acima não é ${0}$ .

Ainda ${a\geq b}$ equivale a ${b\leq a}$ e ${a>b}$ equivale a ${b<a}$ . A relação ${\leq}$ é

reflexiva ${\forall a\in{\mathbb N}}$ , ${a\leq a}$ , pois
$\displaystyle a=a+0;$

anti-simétrica ${\forall a,b\in{\mathbb N}}$ , se ${a\leq b}$ e ${b\leq a}$ então ${b=a}$ , pois existem naturais ${m,n}$
$\displaystyle \begin{array}{rcl} a\leq b &\Rightarrow& a+m=b\\ b\leq a &\Rightarrow& b+n=a \end{array}$

portanto ${(a+m)+n=a}$ , donde ${a+(m+n)=a}$ por associatividade da soma, usando a lei cancelativa ${m+n=0}$ e disso sabemos que ${m=n=0}$ (teo. 1, item 5);

transitiva ${\forall a,~b,~c\in{\mathbb N}}$ , se ${a\leq b}$ e ${b\leq c}$ então ${a\leq c}$ , pois
$\displaystyle \begin{array}{rcl} a\leq b &\Rightarrow& a+m=b\\ b\leq c &\Rightarrow& b+n=c \end{array}$

portanto ${(a+m)+n=c}$ , donde ${a+(m+n)=c}$ , portanto, ${a\leq c}$ .

Teorema 2 Para quaisquer ${a,b\in{\mathbb N}}$ , ${a\leq b}$ ou ${b\leq a}$ .

Demonstração: Para um dado natural ${b}$ definimos

$\displaystyle X_b := \{n \colon n\leq b\} \cup \{n \colon b \leq n\}.$

Vamos mostrar que ${X_b={\mathbb N}}$ , assim ${a\in X_b}$ portanto ${a\leq b}$ ou ${b\leq a}$ .

Como ${ 0 \leq b}$ temos ${0+b = b}$ , assim ${0\in X_b}$ .

Seja ${n\in X_b}$ , então ${n\leq b}$ ou ${ b \leq n}$ . Se ${n\leq b}$ então existe ${r}$ tal que ${n+r=b}$ . Caso ${r=0}$ , de ${n=b}$ temos ${s(n) =b+1 \in X_b}$ pois ${b\leq b+1}$ . Caso ${r\neq 0}$ existe ${u}$ tal que ${r=s(u)}$ . De ${n+s(u) = b}$ temos ${s(n)+u =b}$ , portanto ${b\leq s(n)}$ , logo ${s(n)\in X_b}$ .

Se ${ b \leq n}$ , então ${b+t = n}$ para algum ${t}$ , donde ${s(n) = s(b+t)=b+s(t)}$ , isto é, ${b\leq s(n)}$ portanto ${s(n) \in X_b}$ . Pelo axioma da indução ${X_b={\mathbb N}}$ . $\Box$

Exercício 6 (Lei da tricotomia em ${{\mathbb N}}$ ) Para quaisquer ${a,b\in{\mathbb N}}$ , vale uma e só uma das relações

$\displaystyle a=b, ~a<b,~ b<a$

Solução: Dados naturais ${a}$ e ${b}$ , pelo teorema acima ${a\leq b}$ ou ${b\leq a}$ . Logo existem naturais ${m,n}$ tais que ${a + m = b}$ ou ${b + n = a}$ . Suponhamos ${a\neq b}$ . Então ${m,n\neq 0}$ , ou seja, ${a < b}$ ou ${b < a}$ .

Vamos mostrar a exclusividade.

Se ${a < b}$ e ${b < a}$ então ${a+n=b}$ e ${b+m=a}$ para ${n}$ e ${m}$ naturais diferentes de ${0}$ . De ${a+n=b}$ e ${b+m=a}$ concluímos que ${(b+m) + n = b}$ (substituindo a segunda na primeira); pela associativa ${b+(m+ n) = b}$ , pela cancelativa, ${m+n=0}$ pelo item 1 ${m=n=0}$ . Uma contradição.

Se ${a < b}$ e ${a = b}$ então ${a+n=b}$ e ${a = b}$ então ${n = 0}$ . Uma contradição.

Se ${a > b}$ e ${a = b}$ então, analogamente, derivamos uma contradição. $\Box$

Exercício 7 Mostre que ${\leq}$ é compatível com a adição, i.e.,

$\displaystyle a\leq b \Rightarrow a+c \leq b+c \qquad(\forall c) \ \ \ \ \ (10)$

e é compatível com a multiplicação, i.e.,

$\displaystyle a\leq b \Rightarrow a\cdot c \leq b\cdot c\qquad(\forall c). \ \ \ \ \ (11)$

Exercício 8 Deduza de (10) o item 4 do teorema 1.

Exercício 9 Se ${a<b}$ então ${a+1 \leq b}$ . Prove a recíproca.

Solução: Se ${a<b}$ então ${a+r=b}$ com ${r\neq 0}$ . Existe ${n}$ tal que ${r=n+1}$ . Assim ${a+(n+1)=b}$ , porém ${a+(n+1)= a+(1+n)=(a+1)+n}$ e de ${(a+1)+n=b}$ temos ${a+1 \leq b}$ . $\Box$

Obs.: ${n<p<n+1}$ denota: ${n<p}$ e ${p<n+1}$

— Subtração em ${{\mathbb N}}$ —

Definimos

$\displaystyle b-a := c, \text{ sempre que } a\leq b \text{ em que }c \text{ \'e o natural tal que }a+c=b \ \ \ \ \ (14)$

${c}$ existe por definição de ${\leq}$ . Portanto, para quaisquer ${a,b,c}$ com ${a\leq b}$

$\displaystyle b-a = c \Leftrightarrow b=a+c \ \ \ \ \ (15)$

Como ${a\leq a}$ , está definido ${a-a}$ que, por (15), vale ${a-a=0}$ . Por definição ${b=a+(b-a)}$ .

Proposição 4 Para quaisquer ${a,b,c}$ com ${a\leq b}$ vale ${ c\cdot (b-a) = c\cdot b - c\cdot a .}$

Demonstração: Primeiro, verifiquemos que ${c\cdot b - c\cdot a}$ está definido. De fato, pela compatibilidade da multiplicação com a relação de ordem, exercício 7, ${a\leq b \Rightarrow a\cdot c \leq b\cdot c}$ . Agora, pela definição de ${\leq}$ , existe um natural ${d}$ tal que ${ a + d = b}$ , portanto, ${c\cdot (a+d)= c\cdot b}$ ; deduzimos, usando os itens 8, 10 e 8 do teorema 1

$\displaystyle c\cdot(a+d)= (a+d)\cdot c = a\cdot c+d\cdot c =c\cdot a + c\cdot d$

portanto

$\displaystyle c\cdot a + c\cdot d = c\cdot b$

e por (15)

$\displaystyle c\cdot b - c\cdot a = c\cdot d$

e a proposição segue do fato de que ${d = b-a}$ por (15) e pela escolha de $d$ . $\Box$

— Exercícios —

Prove os itens 6,7,9 e 10 do teorema 1.
Prove que a multiplicação tem ${1}$ como único elemento neutro.
Seja ${a\neq 0}$ . Mostre que a potência ${a^n}$ está definida para todo ${n\in{\mathbb N}}$ se
$\displaystyle \begin{array}{rcl} a^0 &:=& 1\\ a^{s(n)} &:=& a\cdot a^n \end{array}$

Prove que ${a\leq b \Rightarrow a^n \leq b^n}$ .
Prove que não existem ${a,b\in{\mathbb N}\setminus \{0\}}$ com ${a+b=1}$ .
Mostre que o fatorial, ${n!}$ , está definido para todo ${n\in{\mathbb N}}$ se
$\displaystyle \begin{array}{rcl} 0! &:=& 1\\ (n+1)! &:=& (n+1)\cdot n! \end{array}$

Mostre que todo número natural pode ser expresso como soma de potências distintas de ${2}$
Sejam ${a,b,c}$ naturais tais que esteja definido ${a-(b-c)}$ . Mostre que ${(a+c)-b}$ está bem definido e ${a-(b-c) = (a+c)-b}$ .
Sejam ${a,b,c}$ naturais tais que ${b+c\leq a}$ . Mostre que ${a-(b+c)}$ e ${(a-b)-c}$ estão bem definidos e ${a-(b+c)=(a-b)-c}$ .
Sejam ${a,b,c}$ naturais tais que ${0<c<b<a}$ . Mostre que ${0< b-c <a-c < a}$ .
Sejam ${a,b,c}$ naturais tais que ${a\leq c}$ e ${b\leq c}$ . Mostre que, se ${c-a \leq c-b}$ então ${b\leq a}$ .
Prove que ${s(m-1)=m}$ , sempre que ${m-1}$ eestá definido.

Compartilhe isso:
Compartilhar
E-mail
Twitter
Curtir Carregando...

Relacionado

4 respostas em “bc1405 – Números Naturais”

valdefran Alves dos Santos em 11/03/2016 às 2:18 PM disse:

Poderia me passar as respostas dos exercícios 7.8,9,10,11?

Comentar ↓
- jairdonadelli em 15/03/2016 às 8:12 AM disse:
  
  não tenho as respostas digitadas.
  
  Comentar ↓
Eduardo em 04/08/2017 às 8:26 AM disse:

Saudações. Estou a um tempo tentando provar a comutatividade da multiplicação e ainda não obtive exito. ab = ba. Por indução mostrei que 1 * a = a * 1 para todo a natural, semelhante a prova da adição. Depois tentei a indução em b, mas não consegui. Quando tomei um k tal que
ak = ka
precisava mostrar que a(k+1) = (k+1)a. Não consegui mostrar essa ultima parte. Tentei indução em a, mas nem faz muito sentido esse caminho. Pode me ajudar? Aguardo ansioso.

Comentar ↓
- jairdonadelli em 27/02/2018 às 7:57 PM disse:
  
  ${a(k+1) = ak+a1 = ka+1a = (k+1)a}$
  
  Comentar ↓

Notas de aula

Jair Donadelli

bc1405 – Números Naturais

4 respostas em “bc1405 – Números Naturais”

Deixe um comentário Cancelar resposta