bc1405 – Congruências

— Congruências —

Para inteiros ${a,b,n}$ , com ${n\neq 0}$ , dizemos que ${a}$ é congruente a ${b}$ módulo ${n}$ , e escrevemos

$\displaystyle a\equiv b \pmod n \ \ \ \ \ (44)$

se ${n|(a-b)}$ . Como ${n|(a-b) \Leftrightarrow -n|(a-b)}$ nos restringiremos ao caso ${n>0}$ . O caso ${n=1}$ é trivial pois quaisquer dois inteiros são congruentes. Geralmente, os casos interessantes são para ${n>1}$ . Para ${n=2}$ , por exemplo, dois inteiros são congruentes se, e só se, eles diferem por um inteiro par, ou seja, têm mesma paridade.

Por exemplo, ${152 \equiv 5 \pmod 7}$ ( ${152=21\cdot 7 +5}$ ) e ${-152 \equiv 2 \pmod 7}$ ( ${152=(-22)\cdot 7 +2}$ ). Também, ${7\equiv 15 \pmod 8}$ , ${3\equiv 21 \pmod6}$ .

Dados ${a}$ e ${b}$ congruentes, usando o Teorema da Divisão, dividimos ambos por ${n}$ e temos únicos ${q_a,r_a,q_b,r_b}$ tais que ${a=nq_a+r_a}$ e ${b=nq_b+r_b}$ de modo que ${0\leq r_a,r_b<n}$ , portanto, ${-n < r_a - r_b < n}$ e temos

$\displaystyle a-b = n(q_a-q_b) + (r_a - r_b) \ \ \ \ \ (45)$

com ${n|(a-b)~\text{ e }~n|n(q_q-q_b)}$ logo ${n|(r_a-r_b)}$ e como o único múltiplo de ${n}$ que satisfaz ${-n < r_a-r_b < n}$ é o ${0}$ temos

$\displaystyle r_a=r_b.$

Concluindo, se ${a}$ é congruente a ${b}$ módulo ${n}$ então ${a}$ e ${b}$ deixam o mesmo resto quando divididos por ${n}$ . Por outro lado, se ${a}$ e ${b}$ deixam o mesmo resto quando divididos por ${n}$ então ${n|(a-b)}$ pois ${a-b = n(q_a-q_b)}$ . O que estabelecemos foi

Proposição 24 ${a\equiv b \pmod n \Longleftrightarrow a\mod n = b\mod n}$ .

Observação 2 Segue da equivalência dada na proposição acima e do Teorema da Divisão que todo inteiro é congruente a um, e somente um, dentre os números ${\{0,1,2,\dots,n-1\}}$

Claramente, ${\equiv \pmod n}$ é uma relação de equivalência; é reflexiva ( ${a\equiv a \pmod n}$ ), é simétrica ( ${a\equiv b \pmod n \Leftrightarrow b\equiv a \pmod n}$ ), e é transitiva ( ${a\mod n = b\mod n ~\text{ e }~b\mod n = c\mod n \Leftrightarrow a\mod n = c\mod n }$ ).

Proposição 25 ${\equiv}$ é uma relação de equivalência sobre ${{\mathbb Z}}$ .

Além de ser relação de equivalência, congruência é compatível com as operações aritméticas dos inteiros.

Proposição 26 Para quaisquer inteiros ${a,b,c,d,n}$ , se ${a\equiv b\pmod n}$ e ${c\equiv d \pmod n}$ então valem

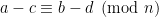
${a+c \equiv b+d \pmod n}$
${a-c \equiv b-d \pmod n}$
${a\cdot c \equiv b\cdot d \pmod n}$

Note que, em particular, vale quando ${c=d}$ .

Demonstração: Da hipótese temos que ${n|(a-b)}$ e ${n|(c-d)}$ e do exercício 31, item 7 temos que ${n|x(a-b)+y(c-d)}$ para quaisquer ${x,y\in{\mathbb Z}}$ , daí

o item 1 segue de ${ (a-b)+ (c-d) = (a+c)- (b+d)}$ ;
o item 2 segue de ${ (a-b) - (c-d) = (a-c)- (b-d)}$ ;
o item 3 segue de ${ c(a-b)+ b(c-d) = ac - bd}$ .

$\Box$

Corolário 27 Para quaisquer inteiros ${a,b,c}$ e ${n>0}$

$\displaystyle a+c \equiv b+c \pmod n \Rightarrow a \equiv b \pmod n.$

Demonstração: Segue do item 2. $\Box$

Corolário 28 Se ${a\equiv b \pmod n}$ , então ${a^k \equiv b^k \pmod n}$ , para todo ${k\in{\mathbb N}}$ .

Demonstração: Segue do item 3. $\Box$

Por exemplo, ${10 \equiv -1 \pmod {11}}$ , portanto ${10^{200} \equiv -1^{200} \pmod {11}}$ , e como ${1 \equiv -1^{200} \pmod {11}}$ temos ${1 \equiv 10^{200} \pmod {11}}$ , portanto, ${11| 10^{200}-1}$ .

Exercício 37 Mostre, usando indução, que para ${n}$ pares de inteiros ${a_i}$ e ${b_i}$ , tais que ${a_i\equiv b_i \pmod n}$ ( ${i\in\{1,2,\dots,n\}}$ ) valem
$\displaystyle {\sum_{i=1}^n a_i \equiv \sum_{i=1}^n b_i \pmod n }$
$\displaystyle { \prod_{i=1}^n a_i \equiv \prod_{i=1}^n b_i \pmod n }$

Proposição 29 Se ${ca \equiv cb \pmod n}$ e ${\mathrm{mdc}(c,n)=d>0}$ então

$\displaystyle a\equiv b \pmod{\frac nd}.$

Demonstração: Se ${ca \equiv cb \pmod n}$ então existe ${q}$ tal que ${nq=ca-cb=c(a-b)}$ . Como ${d>0}$ divide ${n}$ e divide ${c}$ temos ${\frac nd q=\frac cd (a-b)}$ , portanto ${\frac nd | \frac cd (a-b)m }$ mas ${\mathrm{mdc}(\frac nd,\frac cd) =1}$ , portanto ${\frac nd \big| (a-b)}$ . $\Box$

Corolário 30 Se ${\mathrm{mdc}(c,n)=1}$ então

$\displaystyle ac\equiv bc \pmod n \Rightarrow a\equiv b \pmod n .$

Corolário 31 Se ${ca \equiv cb \pmod p}$ e ${p}$ primo que não divide ${c}$ então

$\displaystyle a\equiv b \pmod{p}.$

Exemplo 6 (critério de divisibilidade por 9) Seja ${a_r\dots a_0}$ a representação decimal de ${n}$ . De ${10\equiv 1 \pmod{9}}$ temos, pela proposição 26 que ${10^s \equiv 1 \pmod{9}}$ , ${a\cdot 10^s \equiv a \pmod{9}}$ ${(\forall a)}$ , portanto, pelo exercício 37

$\displaystyle a_0+a_110+a_210^2-\cdots+a_r10^r \equiv a_0+a_1+a_2+\cdots+ a_r \pmod{9}.$

Exemplo 7 (critério de divisibilidade por 11) Seja ${a_r\dots a_0}$ a representação decimal de ${n}$ . De ${10\equiv -1 \pmod{11}}$ temos que ${a\cdot 10^s \equiv a\cdot (-1)^s \pmod{11}}$ portanto

$\displaystyle a_0+a_110+a_210^2-\cdots+a_r10^r \equiv a_0-a_1+a_2-\cdots+(-1)^ra_r \pmod{11}.$

Exemplo
{ISBN} — International Standard Book Number}

Um dos livros texto tem ISBN 8-585-81825-5.

O ISBN tem dez dígitos. O último é um dígito de controle. Os primeiros nove dígitos codificam informações como a língua e a editora do livro. Um código ISBN válido ${ d_0-d_1d_2d_3-d_4d_5d_6d_7d_8-d_9}$ satisfaz

$\displaystyle 10d_0+9d_1+8d_2+7d_3+6d_4+5d_5+4d_6+3d_7+2d_8+1d_9\equiv 0\pmod{11}$

quando ${d_9}$ vale ${10}$ é usado a letra ${X}$ .

Exercício 38 Mostre que ${31|20^{15}-1}$ . (dica: ${20\equiv -11 \pmod{31}}$ )

Demonstração: ${20\equiv -11 \pmod{31}}$ portanto ${20^2 \equiv 121 \equiv - 3 \pmod{31}}$ . Multiplicando as congruências ${20^3 \equiv 33 \equiv 2 \pmod{31}}$ logo ${20^{15} \equiv 2^5 \equiv 1 \pmod{31}}$ . $\Box$

Exercício 39 Qual o resto da divisão de ${{5^3}^{20}}$ por ${13}$ ?

Demonstração: Nas potências de ${5}$

$\displaystyle \begin{array}{rcl} & 5^0 \equiv 1 \pmod{13} & 5^4 \equiv 1 \pmod{13}\\ & 5^1 \equiv 5 \pmod{13} & 5^5 \equiv 5 \pmod{13} \\ & 5^2 \equiv -1 \pmod{13} & 5^6 \equiv -1 \pmod{13} \\ & 5^3 \equiv -5 \pmod{13} & 5^7 \equiv -5 \pmod{13} \; \cdots \end{array}$

os restos se repetem com período ${4}$ . Portanto precisamos conhecer ${3^{20} \mod 4}$ : ${3 \equiv -1 \pmod 4}$ logo ${3^{20} \equiv 1 \pmod 4}$ , portanto ${{5^3}^{20} \equiv 5 \pmod{13}}$ . $\Box$

Exercício 40 Qual os dois últimos algarismos de ${3^{200}}$ .

Demonstração: ${3^{200}=9^{100} = (10-1)^{100}=\sum_{k=0}^{100}\binom{100}k100^{100-k}(-1)^k \equiv -\binom{100}{99}10+\binom{100}{100}\pmod{100}\equiv 1 \pmod{100}}$ . Portanto, ${01}$ . $\Box$

— Sistema completo de restos —

${S\subset {\mathbb Z}}$ é um sistema completo de restos módulo ${n}$ se para todo ${a\in{\mathbb Z}}$ existe um, e só um, ${b\in S}$ tal que ${a\equiv b\pmod n}$ . Por exemplo, alguns sistemas completos de resíduos módulo ${5}$ são os conjuntos:

$\displaystyle \begin{array}{rcl} &\{-2,-1,0,1,2\},\\ &\{0,1,2,3,4\},\\ &\{1,2,3,4,5\},\\ &\{12,24,35,-4,18\}. \end{array}$

Conforme vimos, observação 2, ${\{0,1,\dots,n-1\}}$ é um sistema completo de restos módulo ${n}$ .

Para qualquer sistema completo de restos módulo ${n}$ deve haver uma bijeção com ${\{0,1,\dots,n-1\}}$ (por quê?) logo todo sistema completo de restos módulo ${n}$ tem que ter cardinalidade ${n}$ .

Observação 3 ${\equiv}$ é uma relação de equivalência; uma classe de equivalência é dada por todos os inteiros que deixam o mesmo resto quando divididos por ${n}$ . Um sistema completo de restos é um conjunto formado por um representante de cada classe de equivalência.

Por exemplo, definimos para ${r\in{\mathbb Z}}$

$\displaystyle [r]_n := \{a\in{\mathbb Z}\colon a\equiv r \pmod n\}$

e temos as classes que equivalência módulo ${5}$ dadas por ${[0]_5, ~ [1]_5, ~[2]_5,~ [3]_5,~ [4]_5.}$ Ademais, no exemplo acima identificamos que ${[0]_5=[5]_5=[35]_5}$ , e ${[-2]_5=[3]_5=[18]_5}$ , e ${[-1]_5=[4]_5=[24]_5}$ , e ${[2]_5=[12]_5}$ e ${[-4]_5=[1]_5}$ .

Exemplo 8 A equação ${X^3- 117Y^3 +1 = 5}$ não tem solução inteira. Toda solução inteira da equação deve satisfazer a congruência ${X^3- 117Y^3 +1 \equiv 5 \pmod 9}$ que, Como ${117}$ é múltiplo de ${9}$ , equivale a ${X^3 +1 \equiv 5 \pmod 9}$ a qual não tem solução.

Vejamos, se ${x\in {\mathbb Z}}$ então é congruente a um (e só um) elemento ${r}$ do sistema completo de restos ${\{0,1,2,3,4,5,6,7,8\}}$ , portanto, ${x^3 \equiv r^3 \pmod 9}$ ${(r\in S)}$ e

${r}$ ${0}$ ${1}$ ${2}$ ${3}$ ${4}$ ${5}$ ${6}$ ${7}$ ${8}$

${r^3\mod 9}$ ${0}$ ${1}$ ${8}$ ${0}$ ${1}$ ${8}$ ${0}$ ${1}$ ${8}$

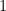
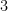
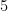
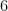
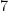
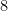
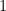
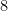
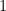
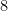
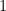
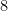
porém nenhum inteiro dentre ${{0,1,8}}$ satisfaz ${X^3 +1 \equiv 5 \pmod 9}$ .
(uma história curiosa a respeito dessa equação pode ser lida na página 81 de COUTINHO, C.; Números inteiros e criptografia RSA. IMPA-SBM, 2009.[512.7 COUn Estante:4H])

Exercício 41 A congruência ${X^2 +1 \equiv 0 \pmod 8}$ não tem solução.

Demonstração: Consideremos o seguinte sistema completo de restos módulo ${8}$ (verifique): ${\{0,\pm 1,\pm 2,\pm 3,4\}}$ . Se ${x\in {\mathbb Z}}$ então existe um único ${r\in \{0,\pm 1,\pm 2,\pm 3,4\}}$ tal que ${x\equiv r \pmod 8}$ , assim ${x^2\equiv r^2 \pmod 8}$ e

${r}$	${ 4}$	${\pm 3}$	${\pm 2}$	${ \pm1}$	${0}$
${r^2\mod 8}$	${0}$	${1}$	${4}$	${ 1}$	${0}$

portanto ${x^2+1}$ é congruente a um dentre ${ 1,2,5}$ . $\Box$

Exercício 42 Sejam ${m_1 , m_2 , \dots , m_k}$ inteiros positivos e defina para todo ${k > 2}$ ,

$\displaystyle \mathrm{mmc}(m_1 , m_2 , \dots , m_k ) := \mathrm{mmc}(\mathrm{mmc}(m_1 , m_2 , \dots , m_{k-1} ), m_k ) \ \ \ \ \ (46)$

Prove que se ${a \equiv b \pmod {m_i}}$ para todo ${i}$ , então

$\displaystyle a \equiv b \pmod{\mathrm{mmc}(m_1 , m_2 , \dots ,m_k )}. \ \ \ \ \ (47)$

— Exercícios —

Sejam ${a,b,r,s}$ inteiros, ${s\neq 0}$ . Prove que ${a\equiv b \pmod r}$ se, e somente se, ${as\equiv bs \pmod {rs}}$ .
Prove que se ${a}$ é um cubo então ${a^2}$ é congruente a ${0}$ , ou ${1}$ , ou ${9}$ , ou ${28}$ módulo 36.
Determinar todos os inteiros positivos ${m}$ tais que as soluções de ${X^2 \equiv 0 \pmod m}$ também sejam soluções de ${X \equiv 0 \pmod m}$ .
Determinar os restos das divisões
1. ${2^{50}}$ por ${7}$ ;
2. ${41^{65}}$ por ${7}$ .
Verifique
1. ${89|(2^{44}-1)}$ ;
2. ${97|(2^{11}-1)}$ .
Qual os dois últimos algarismos de ${7^{7^{100}}}$ . (dica: ${7^k \mod 100}$ é periódico)