bc0406 – Variáveis aleatórias discretas

Se uma moeda é lançada 3 vezes com os resultados independentes. Qual é o número de caras ocorridas? Qual é a probabilidade de termos 2 caras?

resultado 1	resultado 2	resultado 3	Nº de caras
Ca	Ca	Ca	3
Ca	Ca	Co	2
Ca	Co	Ca	2
Ca	Co	Co	1
Co	Ca	Ca	2
Co	Ca	Co	1
Co	Co	Ca	1
Co	Co	Co	0

A probabilidade de ocorrerem exatamente 2 caras é ${\frac 38}$ . Muitas vezes estamos mais interessados numa característica numérica de um evento, mais do que no evento propriamente dito, por exemplo

Qual o número de chamadas telefônicas que chegam a uma central em um intervalo de tempo?
Qual a distância da origem de um ponto no círculo unitário?
Qual a altura de um cidadão escolhido?
Qual o tempo de duração de uma lâmpada escolhida da linha de produção?

Essas são grandezas que dependem do resultado de um experimento, são chamadas de variáveis aleatórias.

Uma variável aleatória real (abreviado v.a.) de um modelo probabilístico ${(\Omega,\mathcal A,\mathbb P)}$ é uma função que associa a cada elemento de um espaço amostral ${\Omega}$ um número real

${ X\colon \Omega \rightarrow {\mathbb R}}$

de modo que

${[X\leq a]= \{\omega\in \Omega \colon X(\omega) \leq a\}}$ ( ${\forall a\in\mathbb R}$ )

é evento do modelo para todo ${a\in {\mathbb R}}$ e cuja probabilidade é denotada ${\mathop{\mathbb P}(X\leq a)}$ . Comumente, usamos as letras maiúsculas finais do alfabeto ${X,Y,Z,W}$ para variáveis aleatórias.

Exercício Assuma que ${[X\leq a]}$ ( ${\forall a\in\mathbb R}$ ) é evento de um modelo probabilístico e prove que são eventos: ${[X>a]}$ , ${[b< X \leq a]}$ , ${[X=a]}$ , ${[X\geq a]}$ , ${[X< a]}$ .

Exemplo 38 Se ${X}$ é o número de caras em 3 lançamentos de uma moeda então

${X\big((\mathrm{Ca,Ca,Ca}) \big) = 3}$
${X\big((\mathrm{Ca,Ca,Co}) \big) = 2}$
${X\big((\mathrm{Ca,Co,Ca}) \big) = 2}$
${X\big((\mathrm{Ca,Co,Co}) \big) = 1}$
${X\big((\mathrm{Co,Ca,Ca}) \big) = 2}$
${X\big((\mathrm{Co,Ca,Co}) \big) = 1}$
${X\big((\mathrm{Co,Co,Ca}) \big) = 1}$
${X\big((\mathrm{Co,Co,Co}) \big) = 0}$

A probabilidade de termos 2 caras é a probabilidade do evento ${X^{-1}(2)}$ que é o conjunto ${\{(\mathrm{Ca,Ca,Co}), (\mathrm{Ca,Co,Ca}), (\mathrm{Co,Ca,Ca})\}}$ .

De modo análogo ao que foi definido acima, definimos os conjuntos ${[X=a]}$ , ${[X < a]}$ , ${[X\leq a]}$ e ${[X\geq a]}$ para uma v.a. ${X\colon \Omega \rightarrow {\mathbb R}}$ . O que nos interessa nas variáveis aleatórias são as probabilidades desses eventos. Também, para um conjunto ${S}$ de números reais ${[X\in S]}$ denota ${\{\omega\in \Omega \colon X(\omega) \in S\}}$ . Com essa notação, se ${X,Y\colon \Omega \rightarrow {\mathbb R}}$ são duas v.a. então temos, por exemplo

${ [X > 3] = \overline{ [X\leq 3] } = \overline{\big\{\omega\in \Omega \colon X(\omega) \leq 3\big\}}= {\big\{\omega\in \Omega \colon X(\omega) > 3\big\}}}$ ;
${ [X\leq 3]\cap [X\geq 3] = [X=3] }$ , e ${[X < 3]\cap [X > 3] = \emptyset}$ ;
${ [X < 3] \cap [ X \geq 2] = [2 \leq X < 3] = {\big\{\omega\in \Omega \colon 2 \leq X(\omega) < 3\big\}}}$ ;

os eventos ${[Y<1]}$ e ${[Y\geq 1]}$ particionam ${\Omega}$ e, por exemplo, assumindo que têm probabilidade positiva
$\displaystyle \mathop{\mathbb P}(X=3) = \mathop{\mathbb P}(X=3~|~Y<1)\mathop{\mathbb P}(Y<1)+ \mathop{\mathbb P}(X=3~|~Y\geq 1)\mathop{\mathbb P}(Y\geq 1)$

pelo teorema da probabilidade total.

Se ${X}$ é o número de caras em 3 lançamentos de uma moeda então
$\displaystyle [X=2] = \big\{(\mathrm{Ca,Ca,Co}),(\mathrm{Ca,Co,Ca}), (\mathrm{Co,Ca,Ca}) \big\}$

$\displaystyle [X\geq 2] = \big\{(\mathrm{Ca,Ca,Co}),(\mathrm{Ca,Co,Ca}), (\mathrm{Co,Ca,Ca}), (\mathrm{Ca,Ca,Ca}) \big\}$

e ${\mathop{\mathbb P}(X=2 ) = 3/8}$ e ${\mathop{\mathbb P}(X\geq 2 )= 1/2}$ . O evento complementar a ${[X\geq 2]}$ é o evento ${ \overline{[X\geq 2]} = [ X< 2] = \big\{ (\mathrm{Ca,Co,Co}), (\mathrm{Co,Ca,Co}), (\mathrm{Co,Co,Ca}), (\mathrm{Co,Co,Co}) \big\}}$ que ocorre com probabilidade ${\mathop{\mathbb P} ( \,\overline{X\geq 2}\, ) = 1- \mathop{\mathbb P} ( X \geq 2 ) = \frac 12}$ . Se ${A}$ é o evento “o primeiro lançamento foi ${\mathrm{Ca}}$ ” então

$\displaystyle \begin{array}{rcl} \mathop{\mathbb P}(X=2~|~A) &=& \frac{\mathop{\mathbb P}\big([X=2]\cap A \big)}{\mathop{\mathbb P}(A)} \\ &=& \frac{\mathop{\mathbb P}\big( \{(\mathrm{Ca,Ca,Co}), (\mathrm{Ca,Co,Ca})\}\big)} {\mathop{\mathbb P}\big(\{ (\mathrm{Ca,Ca,Ca}), (\mathrm{Ca,Ca,Co}), (\mathrm{Ca,Co,Ca}), (\mathrm{Ca,Co,Co}) \} \big)} \\&=& \frac 12. \end{array}$

$\displaystyle \begin{array}{rcl} \mathop{\mathbb P}(X=2~|~X\geq 2) &=& \frac{\mathop{\mathbb P}\big([X=2]\cap [X\geq 2] \big)}{\mathop{\mathbb P}(X\geq 2)} \\ &= & \frac{\mathop{\mathbb P}\big( \{(\mathrm{Ca,Ca,Co}), (\mathrm{Ca,Co,Ca}), (\mathrm{Co,Ca,Ca})\}\big)} {\mathop{\mathbb P}\big(\{ (\mathrm{Ca,Ca,Ca}), (\mathrm{Ca,Ca,Co}), (\mathrm{Ca,Co,Ca}), (\mathrm{Co,Ca,Ca}) \} \big)} \\&=& \frac 34. \end{array}$

Exemplo 39 Três bolas são aleatoriamente retiradas de um saco com 20 bolas numeradas de 1 a 20. Supondo que todas as seleções são equiprováveis, com que probabilidade pelo menos uma tem número maior ou igual a 18?

Se a maior bola selecionada é maior ou igual a 18, então menos uma tem número maior ou igual a 18 e vice-versa. Seja ${X}$ a maior bola selecionada. ${X}$ é uma v.a.. Queremos determinar com que probabilidade ocorre ${[X=18]}$ ou ${[X=19]}$ ou ${[X=20]}$ , ou seja

$\displaystyle \mathop{\mathbb P} ( X\geq 18) = \mathop{\mathbb P}\big( [X=18] \cup [X=19] \cup [X=20] \big) = \mathop{\mathbb P}\left( X=18\right) + \mathop{\mathbb P}\left(X=19 \right) + \mathop{\mathbb P}\left(X=20 \right)$

a igualdade vem do fato dos eventos serem independentes. A quantidade de seleções de três bolas com a maior igual a ${i}$ é ${\binom{i-1}2}$ pois há ${i-1}$ bolas menores, das quais escolhemos 2. Portanto

$\displaystyle \mathop{\mathbb P}(X=i) = \frac{\binom{i-1}2}{\binom{20}3}$

portanto

$\displaystyle \mathop{\mathbb P} ( X\geq 18) = \frac{\binom{17}2}{\binom{20}3}+ \frac{\binom{18}2}{\binom{20}3}+ \frac{\binom{19}2}{\binom{20}3}\approx 0{,}403.$

— Variáveis aleatórias discretas —

Uma v.a. ${X}$ é discreta se assume valores em um subconjunto enumerável de ${{\mathbb R}}$ , ou seja ${\mathrm{Im}(X)}$ é enumerável. Nesse caso, definimos a função de massa de probabilidade (f.m.p.) para ${X}$ como a função ${p_X\colon {\mathbb R} \rightarrow [0,1]}$ tal que

$\displaystyle p_X(a) \stackrel{\text{\tiny def}}{=} \mathop{\mathbb P}(X=a)$

de modo que se ${\mathrm{Im}(X)= \{x_1,x_2,x_3,\dots,x_n,\dots\}}$ então

$\displaystyle \sum_{i=1}^\infty p_X(x_i)=1.$

De modo geral, para ${S\subset {\mathbb R}}$

$\displaystyle \mathop{\mathbb P}(X\in S) = \sum_{x_i\in S} p_X(x_i)$

em particular, podemos calcular a probabilidade de eventos como $[X\leq t]$ , $[X\geq t]$ e outros a partir da f.m.p..

Por exemplo, no caso do lançamento de 3 moedas, o número de caras tem função de massa

$\displaystyle p_X(x) = \begin{cases} 0 & \text { se } x\neq 0,1,2,3\\ 3/8 & \text { se } x=1 \text{ ou } x=2 \\ 1/8 & \text { se } x=0 \text{ ou } x=3. \end{cases}$

Exemplo 40 Lançamos uma moeda com probabilidade de sair cara igual a ${p}$ até sair cara ou completar ${n}$ lançamentos. O número de lançamentos é uma v.a. que denotamos por ${X}$ . Qual a probabilidade de ${[X=k]}$ ? Assumindo independência no resultado de cada lançamento, cada resultado fixo com ${k<n}$ lançamentos tem probabilidade ${\mathop{\mathbb P}(X=k)= p(1-p)^{k-1}}$ ; agora, há dois resultado possíveis com ${n}$ lançamentos, um que termina com cara e e outro que termina com coroa, cuja probabilidade é ${\mathop{\mathbb P}(X=n) = (1-p)^{n-1}}$ .

Exercício 40 Lançamos uma moeda equilibrada ${n}$ vezes, independentemente. O número de caras é uma v.a. que denotamos por ${X}$ . Determine ${\mathop{\mathbb P}(X=k)}$ .

— Principais modelos discretos —

Variável aleatória de Bernoulli: Na prática, ocorrem muitas situações com experimentos em que interessam apenas dois resultados, por exemplo

uma peça é classificada como boa ou defeituosa;
o resultado de um exame médico é positivo ou negativo;
um paciente submetido a um tratamento é curado ou não da doença;
um entrevistado concorda ou não concorda com a afirmação feita;
no lançamento de um dado ocorre ou não ocorre a face “5”.

Nessas situações podemos representar, genericamente, os resultados do experimento com o espaço amostral

$\displaystyle \Omega = \{ \mathrm{sucesso}, \mathrm{fracasso}\}$

e o modelo probabilístico fica determinado dado ${p=\mathop{\mathbb P}(\mathrm{sucesso})\in[0,1]}$ . Esses experimentos recebem o nome de Ensaios de Bernoulli e a v.a. indicadora do evento “sucesso” é uma variável aleatória de Bernoulli com parâmetro ${p}$ .

A notação

$\displaystyle X \sim \mathrm{Bernoulli}(p)$

indica que ${X}$ é uma v.a. de Bernoulli com parâmetro ${p}$ ; ela assume dois valores

${1}$ se ocorre sucesso,
${0}$ se ocorre fracasso;

sua f.m.p. é

$\displaystyle \mathrm{be}_p(x) = \begin{cases} p^x(1-p)^{1-x} &\text{ se } x\in\{0,1\}\\ 0 &\text{nos outros casos.} \end{cases}$

Variável aleatória Binomial: Consideremos ${n}$ repetições independentes de um Ensaio de Bernoulli. Seja ${X}$ o número de sucessos nas repetições.

Exemplo 41 Um dado equilibrado é lançado 3 vezes. Qual é a probabilidade de se obter a face 5 duas vezes? Se ${S}$ denota sucesso, i.e., “ocorre face 5” e ${F}$ denota fracasso, “não ocorrer face 5” então podemos associar a cada ponto do espaço amostral um elemento de ${\{SSS, SSF, SFS, FSS, SFF, FSF, FFS, FFF\}}$ onde atribuímos ${p = \mathop{\mathbb P}(S) = 1/6}$ e ${1 - p = \mathop{\mathbb P}(F) = 5/6}$ . A função de massa de probabilidade é

${x}$ ${p_X(x)}$

${0}$ ${(1-p)^3}$

${1}$ ${3p(1-p)^2}$

${2}$ ${3p^2(1-p)}$

${3}$ ${p^3}$

e podemos escrever essa função como ${p_X(x) = \binom{3}{x}p^x(1-p)^{3-x}}$ para todo ${x\in\{0,1,2,3\}}$ . Assim, ${\mathop{\mathbb P} (X = 2) = \binom{3}{2}p^2(1-p)^{3-2} = 0{,}0694.}$

Uma variável aleatória binomial de parâmetros ${n\in {\mathbb N}}$ e ${p\in(0,1)}$ é uma v.a. com f.m.p.

$\displaystyle \mathrm{bi}_{n,p}(x) = \begin{cases} \binom{n}{x}p^x(1-p)^{n-x}, &\text{ se } x\in\{0,1,2,\dots,n\}\\ 0 &\text{nos outros casos} \end{cases}$

que pode ser vista como o número de sucessos em ${n}$ ensaios independentes de Bernoulli e com mesma probabilidade ${p}$ de sucesso.

De fato, se ${Y_1,Y_2,\dots,Y_n}$ são as v.a. indicadoras de sucesso em cada um dos ensaios, então ${X=\sum_{i=1}^nY_i}$ é a quantidade de sucessos ocorridos.

A notação

$\displaystyle X \sim \mathrm{Binomial}(n,p)$

indica que ${X}$ é uma v.a. com distribuição binomial com parâmetros ${n}$ e ${p}$ .

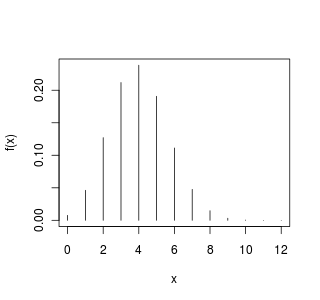
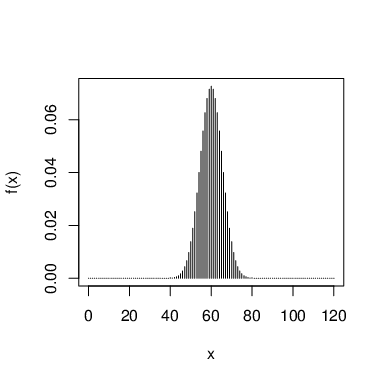
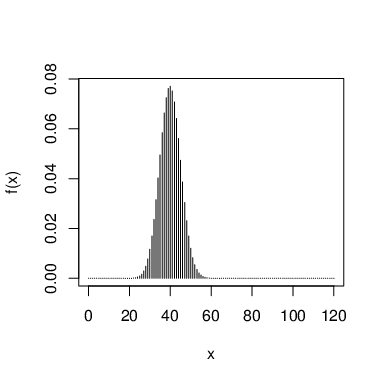
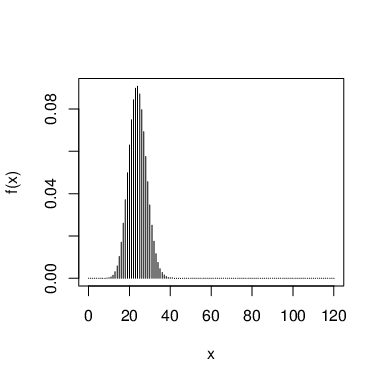
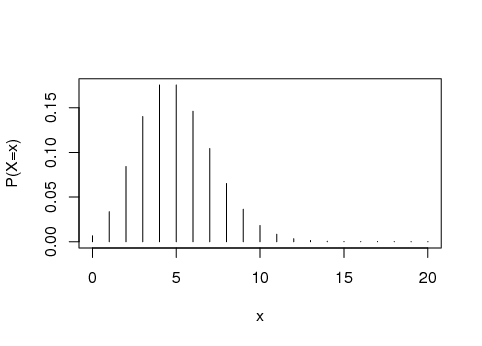
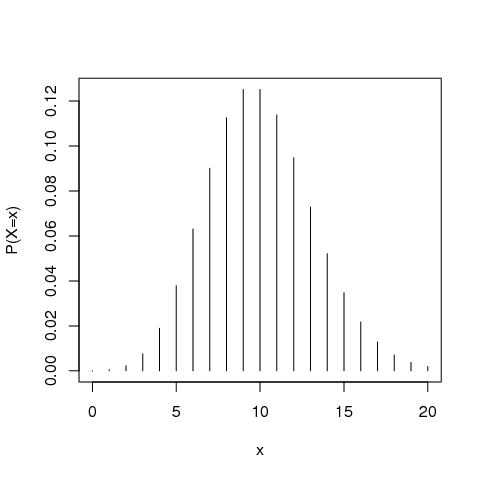
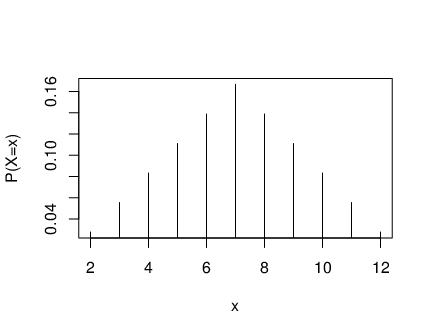
Exemplo 42 Numa prova com 12 questões de múltipla escolha, com 3 alternativas, se todas as respostas forem chute, então a função de massa de probabilidade para o número de acertos ${X\sim \mathrm{Binomial}(12,\frac 13)}$

$\displaystyle f(x) = \mathrm{bi}_{12,\frac 13} =\binom{12}x \left(\frac 13\right)^x \left(\frac 23\right)^{n-x}$

tem o seguinte gráfico de barras

A seguir, respectivamente, os gráficos mostram a distribuição nos casos de uma prova com 120 questões e 2 alternativas, uma prova com 120 questões e 3 alternativas e uma prova com 120 questões e 5 alternativas

Exemplo 43 Um equipamento resiste a um teste de choque com probabilidade ${3/4}$ . Qual é probabilidade de que em ${4}$ testes ${2}$ equipamentos sobrevivam ao choque? Se ${X\sim \mathrm{Binomial}(4,\frac 34)}$

$\displaystyle \mathrm{bi}_{n,\frac 34}(2) = \binom 42 \left(\frac 34 \right)^2 \left(\frac 14 \right)^2 = \frac{27}{128}\approx 0{,}21.$

Exemplo 44 Uma febre atinge 25% dos rebanhos. Se ${X\sim \mathrm{Binomial}(n,\frac 34)}$ animais não ficam doente então

$\displaystyle \mathrm{bi}_{n,\frac 34}(x) = \binom nx (0,75)^x(0,25)^{n-x}$

Os indivíduos de rebanhos de vários tamanhos recebem vacina.

população proporção de sadios

1. ${n=x=10}$ ${\mathop{\mathbb P}(X=x) = 0{,}056}$

2. ${n=x=12}$ ${\mathop{\mathbb P}(X=x) = 0{,}032}$

3. ${n=17,~x=16}$ ${\mathop{\mathbb P}(X\geq x) = 0{,}0501}$

4. ${n=23,~x=21}$ ${\mathop{\mathbb P}(X\geq x) = 0{,}0492}$

e com uma análise rápida e não muito profunda podemos concluir, respectivamente, em cada caso que

se nenhum animal ficar doente, pode ser que a vacina seja eficaz;

se nenhum animal ficar doente, pode ser que a vacina seja eficaz;

se ${\leq 1}$ ficar doente, evidência mais forte de eficácia que 0 doentes em 10 (do caso 1);

${\leq 2}$ doentes em 23 é evidência mais forte que 1 em 17 (caso 3) e 0 em 10 de eficácia.

Exemplo 45 Um fabricante garante que seu produto tem uma taxa de itens defeituosos de ${3\%}$ . Numa selação de 20 itens a serem inspecionados, qual é a probabilidade de ao menos um ser defeituoso? Se ${X}$ é a quantidade de itens defeituosos

$\displaystyle \mathop{\mathbb P}(X\geq 1) = 1-\mathop{\mathbb P}(X=0) = 1- \binom{20}0(0{,}03)^0(0{,}97)^{20} =0{,}4562.$

Se 10 carregamentos por mês deixam a fabrica e de cada carregamento 20 itens são isnpscionados, com que probabilidade 3 carregamentos tem pelo menos um item defeituoso?

$\displaystyle \binom{10}3 (0{,}4562)^3(1-0{,}4562)^7 = 0{,}1602.$

Seja ${X\sim \mathrm{Binomial}(n,p)}$ . Para ${n}$ e ${p}$ fixos, quando ${x}$ varia de ${0}$ a ${n}$ o valor de ${\mathrm{bi}_{n,p}(x)}$ cresce monotonicamente e depois decresce monotonicamente. De fato,

$\displaystyle \frac{\mathrm{bi}_{n,p}(x)}{\mathrm{bi}_{n,p}(x-1)} = \frac{(n-x+1)p}{(1-p)x} \ \ \ \ \ (36)$

que é ${\geq 1}$ se e só se ${(n-x+1)p \geq (1-p)x}$ ou, equivalentemente, ${x\leq (n+1)p}$ .

Proposição 14 Seja ${X\sim \mathrm{Binomial}(n,p)}$ . Para ${n}$ e ${p}$ fixos, quando ${x}$ varia de ${0}$ a ${n}$ o valor de ${\mathrm{bi}_{n,p}(x)}$ cresce monotonicamente e depois decresce monotonicamente atingindo o máximo quando ${x=(n+1)p}$ . ${\Box}$

Variável aleatória de Poisson: a f.m.p. de uma v.a. de Poisson expressa a probabilidade de ocorrência de um determinado número de eventos num intervalo de tempo fixo (ou região do espaço), se estes eventos ocorrem com uma taxa média conhecida e independentemente do tempo desde a última ocorrência. Por exemplo:

o número de erros de impressão numa página de livro;

o número de chamadas que chega a um call center;

o número de partículas ${\alpha}$ descarregadas por um material radioativo em um período fixo de tempo.

A distribuição de Poisson pode ser derivada como um caso limite para a distribuição binomial quando o número de ensaios vai para o infinito e a taxa média de ocorrências permanece fixa. Por isso, pode ser usado como uma aproximação da distribuição binomial se ${n}$ for suficientemente grande e ${p}$ suficientemente pequena, por exemplo, ${n \geq 100}$ e ${np \leq 10}$ .

Há vários exemplos curiosos na literatura. Começaremos com o seguinte exemplo do livro do Feller: Na segunda guerra mundial a cidade de Londres foi intensamente bombardeada pelos alemães. Para determinar se as bombas tinham um alvo ou foram lançadas aleatoriamente os ingleses dividiram o sul da cidade em 576 pequenas regiões, de tamanho ${0{,}25\,\mathrm{km}^2}$ . O total de bombas que atingiram a região foi 537, o que dá uma taxa de 0,9323 bombas por região; se ${n_k}$ é o número de regiões que receberam ${k}$ bombas, a contagem foi

${k}$ ${0}$ ${1}$ ${2}$ ${3}$ ${4}$ ${5}$ ou mais

${n_k}$ 229 211 93 35 7 1

ao qual o modelo de Poisson se ajusta impressionantemente bem, o que levou-os a acreditar que o bombardeio foi aleatório.

William Sealy Gosset, um químico e matemático formado em Oxford, foi contratado, em 1899, pela famosa cervejaria Arthur Guinness and Son em Dublin; sua tarefa era para aperfeiçoar o processo de produção de cerveja. Gosset (que publicou artigos sob o pseudônimo de Student, porque o seu empregador proibiu publicações por funcionários depois que um colega de trabalho havia divulgado segredos comerciais) trabalhou com o modelo de Poisson para a contagem de células de levedura. No artigo sobre tal trabalho, Gosset discutiu “como a dispersão nas contagens de colonias de levedura foi semelhante ao limite exponencial da distribuição binomial”.

Outra aplicação curiosa desta distribuição foi feita por Ladislau Bortkiewicz em 1898, quando lhe foi dada a tarefa de investigar o número de soldados no exército russo morto acidentalmente por coice de cavalo.

A notação

$\displaystyle X \sim \mathrm{Poisson}(\lambda)$

indica que ${X}$ é uma v.a. de Poisson com parâmetro ${\lambda >0}$ , ela conta o número de ocorrências de um determinado evento que ocorre a uma taxa ${\lambda }$ e cuja f.m.p. é dada por

$\displaystyle \mathrm{po}_\lambda(x) = \begin{cases} \frac{\mathrm{e}^{-\lambda}\lambda^x}{x!}, &\text{ se } x\in\mathbb{N}\\ 0 , &\text{ nos outros casos.} \end{cases}$

que pode ser justificada pelo seguinte: a taxa de ocorrência de um evento está relacionada com a probabilidade de um evento ocorrer em pequenos subintervalos, pequenos o suficiente para que a probabilidade de um evento ocorrer duas vezes nesse intervalo é insignificante. Dividimos o intervalo inteiro em ${n}$ subintervalos ${I_1, \dots, I_n}$ de igual tamanho com ${n > \lambda}$ . Isto significa que a probabilidade de ocorrência do evento em um intervalo ${I_k}$ , para cada ${k}$ é igual a ${\lambda / n}$ . Agora, assume-se que as ocorrências do evento em todo o intervalo pode ser visto como ${n}$ ensaios de Bernoulli com parâmetro ${\lambda/n}$ . Suponha que em ${n}$ ensaios independentes de Bernoulli com probabilidade de sucesso ${p=p(n)= \lambda/n}$ , para uma constante ${\lambda >0}$ . A probabilidade de ${x}$ sucessos é ${\mathrm{bi}_{n,\frac{\lambda}n}(x)}$ . Para ${x=0}$

$\displaystyle \mathrm{bi}_{n,\frac{\lambda}n}(0) = \left( 1 -\frac\lambda{n}\right)^n$

portanto, para ${n}$ suficientemente grande ${\mathrm{bi}_{n,p}(0) \approx \mathrm{e}^{-\lambda}}$ (pela definição de ${\mathrm{e}}$ como limite de uma sequência). Agora, usando (36) podemos concluir que

$\displaystyle \begin{array}{rcl} \mathrm{bi}_{n,\frac{\lambda}n}(1) \approx& \mathrm{bi}_{n,\frac{\lambda}n}(0)\lambda &\approx \lambda \mathrm{e}^{-\lambda}\\ \mathrm{bi}_{n,\frac{\lambda}n}(2) \approx& \mathrm{bi}_{n,\frac{\lambda}n}(1)\lambda/2& \approx (\lambda^2/2) \mathrm{e}^{-\lambda}\\ \mathrm{bi}_{n,\frac{\lambda}n}(3) \approx& \mathrm{bi}_{n,\frac{\lambda}n}(2)\lambda/6 &\approx (\lambda^3/3!) \mathrm{e}^{-\lambda} \end{array}$

o que podemos estender usando indução para

$\displaystyle \mathrm{bi}_{n,\frac{\lambda}n}(x) \approx \frac{\lambda^x\mathrm{e}^{-\lambda}}{x!} =\mathrm{po}_\lambda(x)$

que é conhecido como a aproximação de Poisson para a distribuição binomial; em resumo, fixado ${\lambda}$ e fixado ${x}$ , se ${Y_n\sim \mathrm{Binomial}(n,\lambda/n)}$ e ${X\sim \mathrm{Poisson}(\lambda)}$ , então

$\displaystyle \mathop{\mathbb P}(X=x)= \lim_{n\rightarrow\infty} \mathop{\mathbb P}(Y_n=x)$

e uma prova pode ser vista aqui.

Exemplo 46 Um telefone recebe em média 5 chamadas por minuto. Supondo que a distribuição de Poisson seja um modelo adequado para essa situação, qual a probabilidade com que o telefone não receba chamadas durante um intervalo de 1 minuto?

$\displaystyle \mathrm{po}_5(0) = \frac{5^0\mathrm{e}^{-5}}{0!} = 0{,}0067$

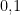
Exemplo 47 O número de partículas que contaminam a superfície de um CD no processo de fabricação tem distribuição de Poisson. O número médio de partículas é ${0{,}1}$ ${\mathrm{particulas}/\mathrm{cm}^2}$ e a área de um CD é ${100\mathrm{cm}^2}$ . Seja ${X}$ o número de partículas num CD; ${X\sim \mathrm{Poisson}(10)}$ .

a probabilidade de ter 12 partículas é
$\displaystyle \mathop{\mathbb P}(X=12)=\frac{\mathrm{e}^{-10}10^{12}}{12!} = 0{,}095$

a probabilidade de ter 0 partículas é
$\displaystyle \mathop{\mathbb P}(X=0) = \frac{\mathrm{e}^{-10}10^0}{0!} = 4{,}54\times 10^{-5}$

a probabilidade de ter ${\leq 12}$ partículas é
$\displaystyle \mathop{\mathbb P}(X\leq 12) = \sum_{x\leq 12} \frac{\mathrm{e}^{-10}10^x}{x!} = 0{,}792$

Exemplo 48 Suponha que essas notas tenham erros tipográficos por página que segue uma distribuição de Poisson com ${\lambda=1/2}$ . Qual é a probabilidade de haver pelo menos um erro nessa página? Se ${X}$ é o número de erros por página

$\displaystyle \mathop{\mathbb P}(X\geq 1) = 1-\mathop{\mathbb P}(X=0)=1-\mathrm{e}^{-1/2}\approx 0{,}393.$

Exercício 41 Prove que a f.m.p. de ${X\sim\mathrm{Poisson}(\lambda)}$ satisfaz

$\displaystyle \mathrm{po}_\lambda(x+1)= \frac{\lambda}{x+1} \mathrm{po}_\lambda(x).$

— Esperança e Variância de v.a. discreta —

Se ${X}$ é uma v.a. discreta com função de massa de probabilidade ${p_X}$ então a esperança, também chamada de valor médio ou valor esperado da v.a. ${X}$ é, simplesmente, a média ponderada dos valores da função de probabilidade

$\mathop{\mathbb E}(X) \stackrel{\text{\tiny def}}{=} \sum_{x}x\cdot p_X(x)$

onde a soma é sobre os valores de ${x}$ tais que ${p_X(x)>0 }$ .

Por exemplo, no caso de uma v.a. constante, digamos ${X(\omega)=c}$ para algum ${c\in {\mathbb R}}$ , temos

$\displaystyle \mathop{\mathbb E} (X) = \sum_{x}x\cdot p_X(x) = c p_X(c) = c.$

Exemplo 53 (variável aleatória indicadora) Seja ${1_A}$ variável aleatória indicadora da ocorrência do evento ${A}$ , i.e., ${1_A=1}$ se ${A}$ ocorre e ${1_A=0}$ se ${\overline A}$ ocorre, ou ainda, para todo ${\omega\in\Omega}$

$\displaystyle 1_A(\omega) = \begin{cases} 1 & \text{ se }\omega\in A;\\ 0 & \text{ se }\omega\not\in A.\\ \end{cases} \ \ \ \ \ (37)$

Então ${\mathop{\mathbb E}(1_A) = 1\mathop{\mathbb P}(A) + 0\mathop{\mathbb P}(\overline A) = \mathop{\mathbb P}(A)}$ .

Notemos que ${1_A \sim \mathrm{Bernoulli}(p)}$ para ${p=\mathop{\mathbb P}(A)}$ e, de fato, vale

Proposição 15 Se ${X\sim \mathrm{Bernoulli}(p)}$ então ${\mathop{\mathbb E}(X)=p}$ .

Exemplo 54 Seja ${X}$ o resultado de um lançamento de um dado,

$\displaystyle \mathop{\mathbb E} X = 1\frac 16 + 2\frac 16 + 3 \frac 16 + 4 \frac 16 + 5\frac 16 + 6\frac 16 = \frac 72.$

Qual a probabilidade ${\mathop{\mathbb P}(X=7/2)}$ ?

Exemplo 55 Num jogo de azar em cada aposta você ganha ${\$ 1.000.000}$ com probabilidade ${p}$ e ${\$10}$ com probabilidade ${1-p}$ . Se ${Y}$ é o ganho numa aposta, então a esperança de ganho numa aposta é

$\displaystyle \mathop{\mathbb E}(Y)= 10^6p+10(1-p).$

No caso de ${p=1/2}$ , temos ${\mathop{\mathbb E}(Y) = 500.005}$ , qual é a probabilidade de você ganhar ${\$500.000}$ numa aposta?

Exemplo 56 Num jogo com 3 moedas, você ganha ${\$5}$ se ocorrerem três caras ou três coroas, você perde ${\$3}$ se ocorrer uma ou duas caras, se ${Y}$ é o ganho numa rodada então a esperança do ganho é

$\displaystyle \mathop{\mathbb E}(Y) = 5\frac 14 - 3\frac 34 =-1.$

Com que probabilidade um jogador ganha ${\$7}$ em três rodadas consecutivas e independentes?

Exemplo 57 Qual é o valor médio da soma dos pontos no lançamento de dois dados? O espaço amostral é composto por 36 eventos elementares igualmente prováveis, se ${X}$ é o resultado da soma dos lançamentos, então sua função de massa de probabilidade é

${x}$ ${2}$ ${3}$ ${4}$ ${5}$ ${6}$ ${7}$ ${8}$ ${9}$ ${10}$ ${11}$ ${12}$

${p(x)}$ ${\frac1{36}}$ ${\frac2{36}}$ ${\frac3{36}}$ ${\frac4{36}}$ ${\frac5{36}}$ ${\frac6{36}}$ ${\frac5{36}}$ ${\frac4{36}}$ ${\frac3{36}}$ ${\frac2{36}}$ ${\frac1{36}}$

O valor esperado da soma é

$\displaystyle \mathop{\mathbb E}(X) = 2\frac 1{36} + 3\frac2{36} + \cdots + 11\frac 2{36} + 12\frac 1{36} = \frac{252}{36} = 7.$

Exemplo 58 ( ${\mathop{\mathbb E}(X)=\infty}$ ) Numa urna estão 1 bola branca e 1 bola preta; uma bola é escolhida ao acaso, se for preta ela é devolvida e mais uma bola preta é colocada na urna e o sorteio é repetido, se sair bola branca o experimento termina. Se ${X}$ é o número de rodadas até terminar então

$\displaystyle \mathop{\mathbb P}(X=k)= \frac 1{k(k+1)}$

e a média é

$\displaystyle \sum_{k=1}^\infty k \frac 1{k(k+1)} = \sum_{k = 2}^\infty \frac 1k = \infty$

(essa é a série harmônica).

Observação 3 No caso do último exemplo dizemos que a variável aleatória não tem esperança finita.

Teorema 16 Se ${X}$ é uma variável aleatória com esperança finita e ${g}$ uma função a valores reais, então ${g(X)}$ é uma variável aleatória e

$\mathop{\mathbb E}(g(X)) = \sum_x g(x)p_X(x)$ .

Demonstração: Definamos ${Y\stackrel{\text{\tiny def}}{=} g(X)}$ e temos

$\displaystyle \mathop{\mathbb E}(Y) = \sum_y y\, \mathop{\mathbb P}(Y=y) = \sum_y y\, \mathop{\mathbb P}(g(X)=y)$

Se ${\omega \in [g(X)=y]}$ então existe um ${x\in {\mathbb R}}$ tal que ${X(\omega)=x}$ e ${g(x)=y}$ e vice-versa, isto é, se ${\omega \in [X=x]}$ para algum ${x}$ tal que ${g(x)=y}$ então ${\omega \in [g(X)=y]}$ , portanto

$\displaystyle \left[g(X)=y\right]=\bigcup_{\substack{x\\g(x)=y}} [X=x]$

em que a união é sobre todo ${x}$ tal que ${g(x)=y}$ e é uma união de eventos mutuamente exclusivos, de modo que

$\displaystyle \begin{array}{rcl} \mathop{\mathbb E}(Y) &=& \sum_y y\, \mathop{\mathbb P}(g(X)=y)\\ &=& \sum_y y \sum_{\substack{x\\g(x)=y}}\mathop{\mathbb P}(X=x)\\ &=& \sum_y \sum_{\substack{x\\g(x)=y}}g(x)\mathop{\mathbb P}(X=x)\\ &=& \sum_xg(x)\mathop{\mathbb P}(X=x) \end{array}$

que é o resultado que queríamos obter. $\Box$

Corolario 17 (Linearidade da esperança) Para quaisquer ${a,b\in{\mathbb R}}$ , vale ${\mathop{\mathbb E}(aX+b) = a\mathop{\mathbb E}(X)+b}$ .

Demonstração: Basta tomar ${g(x) =ax+b}$ no teorema. $\Box$

Exemplo 59 Seja ${X}$ o número de carros lavados num lava-rápido em 1 hora

${x}$ ${4}$ ${5}$ ${6}$ ${7}$ ${8}$ ${9}$

${p_X(x)}$ ${1/12}$ ${1/12}$ ${1/4}$ ${1/4}$ ${1/6}$ ${1/6}$

Para ${x}$ carros lavados o atendente recebe ${2x-1}$ reais do gerente. O ganho médio, por hora, é

$\displaystyle \mathop{\mathbb E}(2X-1) = \sum_{x=4}^9 (2x-1)p_X(x) = 12{,}67.$

— Soma de variáveis aleatórias —

Sejam ${X}$ e ${Y}$ v.a.’s discretas, com esperança finita e definidas sobre o mesmo espaço amostral. A soma delas é a função ${X+Y}$ dada por

$\displaystyle (X+Y) (\omega) \stackrel{\text{\tiny def}}{=} X(\omega)+Y(\omega)$

O valor esperado da soma é ${\mathop{\mathbb E}(X+Y) = \sum_z z \mathop{\mathbb P}(X+Y = z )}$ . Agora,

$\displaystyle \begin{array}{rcl} [X+Y = z ] &=& \big\{\omega\in \Omega \colon X+Y(\omega)=z\big\} \\ &=& \big\{\omega\in \Omega \colon X(\omega)+Y(\omega)=z\big\} \end{array}$

e se ${\mathrm{Im}(X) =\{x_1,x_2,\dots\}}$ e ${\mathrm{Im}(Y) =\{y_1,y_2,\dots\}}$ temos

$\displaystyle \big\{\omega\in \Omega \colon X(\omega)+Y(\omega)=z\big\} = \bigcup_{\substack{(i,j)\\ x_i+y_j=z}} \big\{\omega\in \Omega \colon X(\omega)=x_i\big\}\cap \big\{\omega\in \Omega \colon Y(\omega)=y_j\big\}$

de modo que

$\displaystyle \mathop{\mathbb P}(X+Y = z) = \sum_{\substack{(i,j)\\ x_i+y_j=z}} \mathop{\mathbb P} ([X= x_i ] \cap [Y = y_j ])$

portanto

$\displaystyle \begin{array}{rcl} \mathop{\mathbb E}(X+Y) &=& \sum_z z \mathop{\mathbb{P}}\big(X+Y = z \big) \\ &=& \sum_i\sum_j (x_i+y_j)\mathop{\mathbb P}\big([X=x_i]\cap [Y=y_j]\big) \\ &=& \sum_i\sum_j x_i\mathop{\mathbb P}\big([X=x_i]\cap [Y=y_j]\big)+y_j\mathop{\mathbb P}\big([X=x_i]\cap [Y=y_j]\big) \\ &=& \sum_i\sum_jx_i\mathop{\mathbb P}\big([X=x_i]\cap [Y=y_j]\big)+\sum_j\sum_i y\mathop{\mathbb P}\big([X=x_i]\cap [Y=y_j]\big) \end{array}$

mas

$\displaystyle \sum_j x_i\mathop{\mathbb P}\big([X=x_i]\cap [Y=y_j]\big) = x_i \sum_j \mathop{\mathbb P}\big([X=x_i]\cap [Y=y_j]\big) = x_i \mathop{\mathbb P}\big([X=x_i]\big)$

donde concluímos que ${\mathop{\mathbb E}(X+Y) = \sum_ix_i\mathop{\mathbb P}(X=x_i)+\sum_j y_j\mathop{\mathbb P}(Y=y_j)}$ , isto é

$\mathop{\mathbb E}(X+Y) = \mathop{\mathbb E}(X) + \mathop{\mathbb E}(Y).\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (*)$

Retomando o exemplo 57, se dois dados honestos são lançados e ${X}$ é o resultado do primeiro dado e ${Y}$ o resultado do segundo dado, então o valor esperado para a soma é ${E(X+Y)=\mathop{\mathbb E}(X)+\mathop{\mathbb E}(Y) = \frac72+\frac72 = 7}$ .

Exercício 42 Se ${X_1,\dots,X_n}$ são v.a.’s discretas com esperança finita do mesmo modelo probabilístico então ${\mathop{\mathbb E}(X_1+\cdots+X_n) = \mathop{\mathbb E}(X_1)+\cdots+\mathop{\mathbb E}(X_n)}$ .

Por exemplo, se ${n}$ dados honestos são lançados, então o valor esperado para a soma dos resultados é ${ \mathop{\mathbb E}(X_1+\cdots+X_n) = \mathop{\mathbb E}(X_1)+\cdots+\mathop{\mathbb E}(X_n)= n\frac72}$ , em que ${X_i}$ é o valor do resultado de um lançamento.

Exemplo 60 (Esperança de uma v.a. ${\mathrm{Binomial}(n,p)}$ ) Sejam ${Y_i,Y_2,\dots,Y_n}$ v.a.’s com distribuição de Bernoulli com parâmetro ${p}$ . Então ${X= Y_i+Y_2+\dots+Y_n}$ conta o número de sucesso em ${n}$ ensaios de Bernoulli. Para todo ${i}$ temos ${\mathop{\mathbb E}(Y_i)=p}$ , portanto ${\mathop{\mathbb E}(X)=np}$ .

A proposição 14 ~sugere que os maiores valores de ${\mathrm{bi}_{n, p}}$ (os valores mais prováveis de uma v.a. binomial) estão em torno do valor médio (reveja os gráficos do exemplo 42).

Sejam ${X}$ e ${Y}$ v.a.’s discretas, com esperança finita e definidas sobre o mesmo espaço amostral. O produto delas é ${X\cdot Y(\omega) \stackrel{\text{\tiny def}}{=} X(\omega)\cdot Y(\omega)}$ . Em geral não vale ${\mathop{\mathbb E}(X\cdot Y) = \mathop{\mathbb E}(X)\mathop{\mathbb E}(Y)}$ .

Exemplo 61 ( ${\mathop{\mathbb E}(X\cdot X) \neq \mathop{\mathbb E}(X)\mathop{\mathbb E}(X)}$ ) Seja ${X}$ o resultado do lançamento de um dado, como no exemplo 54.

$\displaystyle \mathop{\mathbb E}(X^2) = \frac{1+4+9+16+25+36}6 = \frac{91}6.$

Notemos que, com o resultado do exemplo 54 podemos concluir que ${\mathop{\mathbb E}(X\cdot X) \neq \mathop{\mathbb E}(X)\mathop{\mathbb E}(X)}$ .

— Variância e desvio padrão —

A variância da v.a. ${X}$ é uma medida de quão dispersos estão os valores que a variável assume com relação ao valor médio. Por exemplo, se ${\mathop{\mathbb P}(X=100)=\mathop{\mathbb P}(X=-100)= 1/2}$ e ${\mathop{\mathbb P}(Y=1)=\mathop{\mathbb P}(Y=-1)= 1/2}$ então ${X}$ e ${Y}$ têm valor esperado ${0}$ mas ${Y}$ assume valores mais próximos da média que ${X}$ . Essa característica não é capturada pelo valor esperado. Uma opção é computar o valor médio da distância entre um valor de ${X}$ e o valor médio ${\mathop{\mathbb E}(X)}$ , isto é, a esperança de ${|X-\mathop{\mathbb E}(X)|}$ , entretanto, uma solução mais conveniente é calcular o valor médio do quadrado desses desvios ${|X-\mathop{\mathbb E}(X)|^2}$ .

A variância de uma variável aleatória ${X}$ de esperança finita é o valor esperado da v.a. ${g(X)=(X-\mathop{\mathbb E}(X))^2}$ , sempre que ${\mathop{\mathbb E}(X)}$ é finito.

$\mathrm{Var}(X) \stackrel{\text{\tiny def}}{=} \mathop{\mathbb E}(X-\mathop{\mathbb E}(X))^2$

Da definição temos

$\displaystyle \mathrm{Var}(X) = \sum_x(x-\mathop{\mathbb E}(X))^2p_X(x)$

e o seguinte exercício fornece um modo, em geral, mais fácil para computar a variância.

Exercício 43 Prove que

${\displaystyle\mathrm{Var}(X) = \mathop{\mathbb E}(X^2) - (\mathop{\mathbb E}(X))^2. }$

O desvio padrão é definido como a raiz quadrada positiva da variância

${\displaystyle\sigma_X = \sqrt{\mathrm{Var} (X )}. }$

Suponhamos que ${X}$ é, por exemplo, a quantidade de refrigerante engarrafada por uma máquina de uma fábrica em ${ml}$ ( ${\mathrm{mililitros}}$ ). Então ${\mathrm{Var}(X)}$ é a dispersão dos valores de ${X}$ com respeito a média em ${ml^2}$ , o desvio padrão é uma medida de dispersão em ${ml}$ .

Exemplo 62 Se ${X~\mathrm{Bernoulli}(p)}$ então ${\mathrm{Var}(X) = \mathop{\mathbb E}(X^2) -(\mathop{\mathbb E}(X))^2 = p-p^2}$ pois ${\mathop{\mathbb E}(X^2) = 1^2 p + 0^2(1-p)=p}$ .

Exemplo 63 A variância no valor resultante de um lançamento de dado é (veja os exemplos 54 e 61) ${35/12 \approx 2,91}$ . O desvio padrão é ${\approx 1,7}$ .

Exemplo 64 Retomando o exemplo 57, se ${X}$ é o resultado da soma do lançamento de dois dados, então o valor esperado da soma é ${7}$ e o da variância é

$\displaystyle \begin{array}{rcl} \mathrm{Var} (X) &=& (2 - 7)^2(1/36) + (3 - 7)^2(2/36) + \cdots \\ &&+ (11- 7)^2(2/36) + (12- 7)^2(1/36)= \frac{210}{36} = 5,83. \end{array}$

o desvio padrão vale ${2,41}$ , aproximadamente. Notemos que no intervalo ${(\mathop{\mathbb E}(X) -\sigma_X,\mathop{\mathbb E}(X) + \sigma_X)= \{5,6,7,8,9\}}$ está concentrado ${2/3}$ da massa de probabilidade.

Exemplo 65 Um canal digital transmite informação em pacotes de 4 bits. Os bit podem ser recebidos com erro e ${X}$ denota o número de bits errados num pacote, com função de massa de probabilidade

${\mathop{\mathbb P}(X=0) = p(0) = 0,6561}$

${\mathop{\mathbb P}(X=1) = p(1) = 0,2916}$

${\mathop{\mathbb P}(X=2) = p(2) = 0,0486}$

${\mathop{\mathbb P}(X=3) = p(3) = 0,0036}$

${\mathop{\mathbb P}(X=4) = p(4) = 0,0001}$

e o valor médio do número de bits errados é

$\displaystyle \begin{array}{rcl} \mathop{\mathbb E}(X) &=& 0\cdot p(0)+1\cdot p(1)+2\cdot p(2)+3\cdot p(3)+4\cdot p(4)\\ &=& 0\cdot 0,6561 + 1\cdot 0,2916 + 2\cdot 0,0486 + 3\cdot 0,0036 +4 \cdot 0,0001\\ &=& 0,4 \end{array}$

e a variância

$\displaystyle \begin{array}{rcl} \mathrm {Var}(X) &=& \sum_{x=0}^4(x - \mathop{\mathbb E}(X))^2p(x) \\ &=& 0,16\cdot 0,6561 + 0,36\cdot 0,2916 + 2,56\cdot 0,0486 + 6,76 \cdot 0,0036 \\&&+ 12,96 \cdot 0,001296 \\&=& 0,36 \end{array}$

portanto o desvio padrão é ${0,6}$ .

Proposição 18 Se ${X}$ , ${Y}$ são v.a.’s discretas com esperança finita e ${a,b\in R}$ , então

${\mathrm{Var}(aX+b) = a^2 \mathrm{Var}(X)}$

${\mathrm{Var}(X+Y) = \mathrm{Var}(X)+\mathrm{Var}(Y) +2(\mathop{\mathbb E}(XY)-\mathop{\mathbb E}(X)\mathop{\mathbb E}(Y))}$ .

Demonstração: Sejam ${X}$ , ${Y}$ , ${a}$ , ${b}$ como no enunciado e vamos usar a notação ${\mu_X=\mathop{\mathbb E}(X)}$ e ${\mu_Y=\mathop{\mathbb E}(Y)}$ . Abaixo usamos várias vezes a linearidade da esperança, corolário 17 e equação (*)

${\mathrm{Var}(aX+b) = \mathop{\mathbb E}((aX+b)^2) -(\mathop{\mathbb E}(aX+b))^2}$ . Do primeiro termo deduzimos ${\mathop{\mathbb E}((aX+b)^2)=}$
$\displaystyle \mathop{\mathbb E}(a^2 X^2 + 2 ab X+b^2) = \mathop{\mathbb E}(a^2 X^2) + \mathop{\mathbb E}(2 ab X) + \mathop{\mathbb E}(b^2) = a^2\mathop{\mathbb E}(X^2) + 2ab\mu_X + b^2$

e do segunda termo ${ (\mathop{\mathbb E}(aX+b))^2= (a\mathop{\mathbb E}(X) +b)^2 = a^2 \mu_X^2 + 2ab\mu_X +b^2}$ , portanto

$\displaystyle \mathrm{Var}(aX+b) = a^2\mathop{\mathbb E}(X^2) -a^2 \mu_X^2 = a^2(\mathop{\mathbb E}(X^2) - (\mathop{\mathbb E}(X))^2)= a^2 \mathrm{Var}(X).$

Usando a definição ${\mathrm{Var}(X+Y) = \mathop{\mathbb E}\big( (X+Y - \mathop{\mathbb E}(X+Y))^2 \big)}$
$\displaystyle \begin{array}{rcl} \mathrm{Var}(X+Y) &=&\mathop{\mathbb E}\big( (X+Y - \mathop{\mathbb E}(X+Y))^2 \big)\\&=& \mathop{\mathbb E}\big( (X - \mathop{\mathbb E}(X) ) + (Y - E(Y)) \big)^2 \\&=& \mathop{\mathbb E}\big( (X - \mathop{\mathbb E}(X) )^2 + (Y - E(Y))^2 + 2((X - \mathop{\mathbb E}(X))(Y - E(Y)) \big) \\ &=& \mathop{\mathbb E}\big( (X - \mathop{\mathbb E}(X) )^2 \big) +\mathop{\mathbb E}\big( (Y - E(Y))^2\big) +\mathop{\mathbb E}\big( 2((X - \mathop{\mathbb E}(X))(Y - E(Y)) \big) \\ &=& \mathrm{Var}(X) + \mathrm{Var}(Y) +\mathop{\mathbb E}\big( 2((X - \mathop{\mathbb E}(X))(Y - E(Y)) \big) \\&=& \mathrm{Var}(X) + \mathrm{Var}(Y) + 2\big( \mathop{\mathbb E}(XY) -\mathop{\mathbb E}(X)\mathop{\mathbb E}(Y) \big) \end{array}$

pois ${\mathop{\mathbb E}\big( 2((X - \mathop{\mathbb E}(X))(Y - E(Y)) \big) = 2 \mathop{\mathbb E}\big( XY -X\mathop{\mathbb E}(Y) -Y\mathop{\mathbb E}(X) +\mathop{\mathbb E}(X)\mathop{\mathbb E}(Y) \big) }$ e como ${\mathop{\mathbb E}(X\mathop{\mathbb E}(Y)) = \mathop{\mathbb E}(Y\mathop{\mathbb E}(X)) = \mathop{\mathbb E}(X)\mathop{\mathbb E}(Y) }$ os termos do meio se cancelam.

$\Box$

O termo ${\mathop{\mathbb E}(XY)-\mathop{\mathbb E}(X)\mathop{\mathbb E}(Y)}$ no item 2 do resultado acima é chamado de covariância de ${X}$ e ${Y}$ e denotado ${\mathrm{cov}(X,Y)}$ .

— Exercícios —

Seja ${X}$ uma v.a. discreta que assume valores em ${{\mathbb N}}$ . Prove que
$\displaystyle \mathop{\mathbb E}(X) = \sum_{i\geq 1} \mathop{\mathbb P}(X \geq i).$

Uma v.a. ${X}$ tem distribuição geométrica com parâmetro ${p}$ , ${X\sim \mathrm{Geometrica}(p)}$ , se a f.m.p. dada por
$\displaystyle \mathrm{ge}_p(x) = (1-p)^{x-1}p, \qquad \forall x\in\{1,2,\dots\}$

que correspondente ao número de ensaios de Bernoulli independentes com parâmetro ${p}$ até ocorrer um sucesso. Prove que

$\displaystyle \mathop{\mathbb E} (X) = \frac 1p .$

(Dica: use o exercício 1)

Prove que ${X\sim \mathrm{Geometrica}(p)}$ é sem memória, isto é, $\mathbb{P}(X\geq a+b ~|~ X\geq b) = \mathbb{P}(X\geq a)$ .

Se ensaios de Bernoulli com probabilidade de sucesso ${p}$ são realizados de modo independentemente até que hajam ${r}$ sucessos. Qual é a probabilidade de serem necessários ${n}$ ensaios ( ${n\geq r}$ )?

Se ensaios de Bernoulli com probabilidade de sucesso ${p}$ são realizados de modo independentemente, qual é a probabilidade de que ${r}$ sucessos ocorram antes que ${m}$ fracassos?

Em um teste de múltiplas escolhas com 3 respostas possíveis para cada uma das 5 questões, com que probabilidade um estudante acerte pelo menos 4 questões apenas chutando?

Quatro jogadas independentes de uma moeda honesta são feitas. Seja ${X}$ o número de caras. Determine a fmp de ${X-2}$ .

Um sujeito se alega paranormal. Num teste, uma moeda honesta é jogada 10 vezes e pede-se ao homem a previsão dos resultados. Ele acerta 7 respostas. Qual é a probabilidade desse evento supondo que o homem chuta cada previsão?

Um livro de jogos de azar recomenda o seguinte para ganhar na roleta: aposte 1 real no vermelho, se der vermelho (probabilidade 18/38) pegue o lucro de 1 real e desista. Se perder a aposta (probabilidade 20/38) faça apostas adicionais de 1 real no vermelho nos próximos dois giros e depois desista. Seja ${X}$ o lucro obtido com essa estratégia.

determine ${\mathop{\mathbb P}(X>0)}$ ;

essa é uma estratégia de vitória?

calcule ${\mathop{\mathbb E}(X)}$ .

Você tem R$1.000,00 e uma mercadoria é vendida a R$2,00 o quilo. Na semana que vem a mesma mercadoria estará sendo vendida a R$1,00 ou R$4,00, com igual probabilidade.

Se você quer maximizar a quantidade esperada de dinheiro que terá no fim de semana, qual estratégia empregar?

Se você quer maximizar a quantidade esperada de mercadoria que terá no fim de semana, qual estratégia empregar?

Um motor de avião tem probabilidade ${1-p}$ de falhar durante o voo, de forma independente dos outros motores. Se o avião precisa da maioria dos motores para terminar o voo de forma segura, para quais valores de ${p}$ é preferível um avião de 5 motores a um de 3?

Uma moeda com probabilidade ${p}$ par cara é lançada 10 vezes. Dado que o número de caras é 6 qual é a probabilidade com que os 3 primeiros resultados são

cara,coroa,coroa

coroa,cara, coroa

Se ${X}$ tem distribuição binomial com média 6 e variância 2,4 determine ${\mathop{\mathbb P}(X=5)}$ .

Uma companhia de seguros vende uma apólice dizendo que uma quantidade ${A}$ de dinheiro deve ser paga se um determinado evento ${E}$ ocorra em uma ano. Estima-se que ${E}$ ocorra em uma no com probabilidade ${p}$ . Qual é o preço da apólice se o lucro esperado da companhia é 10%?

paradigma de Poisson: Consideremos ${n}$ eventos sendo que o evento ${i}$ ocorre com probabilidade ${p_i}$ . Se os valores de ${p_i}$ são pequenos e o eventos independentes (“fracamente dependentes”) então os eventos que ocorrem têm aproximadamente distribuição de Poisson com parâmetro ${\sum_{i=1}^n p_i}$ .Em resposta a um ataque de 10 mísseis, um contra-ataque de 500 mísseis antiaéreos é efetuado de modo que o alvo de um míssil antiaéreo é qualquer um dos 10 mísseis, independentemente, com probabilidade 0,1. Use o paradigma de Poisson para determinar uma aproximação para a probabilidade de todos os 10 mísseis serem atingidos.

Os times ${A}$ e ${B}$ jogam uma série de partidas. O vencedor é aquele que ganhar primeiro 3 partidas. ${A}$ vence cada partida com probabilidade ${p}$ independentemente das outras partidas. Qual é a probabilidade condicional de que ${A}$ vença

a série dado que tenha ganho a primeira partida;

a primeira partida dado que ganhou a série.

Cada um dos membros de um corpo de 7 jurados toma a decisão correta com probabilidade 0,7, de forma independente um dos outros. Se a decisão do corpo é feita pela regra da maioria, com que probabilidade a decisão correta é tomada? Dado que 4 juízes tenham a mesma opinião dos jurados, qual é a probabilidade dos jurados tomarem a decisão correta?

O número de ovos que um inseto deposita numa árvore é uma v.a. de Poisson com parâmetro ${\lambda}$ . Entretanto, tal variável só pode ser observada se for positiva, pois se for 0 não se sabe dizer se o inseto esteve na árvore. Se ${Y}$ é o número de ovos depositados então
$\displaystyle \mathop{\mathbb P}(Y=i) = \mathop{\mathbb P}(X=i ~|~ X>0)$

para ${X\sim \mathrm{Poisson}(\lambda)}$ . Determine ${\mathop{\mathbb E}(Y)}$ .

A pessoas de ${n}$ casais sentam-se aleatoriamente em uma mesa redonda. ${C_i}$ representa o evento “o par do casal ${i}$ estão sentados um ao lado do outro”. ${(i)}$ Determine ${P(C_i)}$ ; ${(ii)}$ determine ${\mathop{\mathbb P}(C_i ~|~C_j)}$ para ${i\neq j}$ ; determine o valor aproximado, para ${n}$ grande, de que nenhum par de casal esteja sentado um ao lado do outro.

Numa roleta com números de 0 a 36 e um 00 João sempre aposta nos números de 1 a 12. Com que probabilidade

João perde suas 5 primeira apostas;

sua primeira vitória ocorra na quarta aposta.

Suponha que se saiba que o número de carros que chegam a um cruzamento específico durante um período de tempo de 20s é caracterizado pela função de massa
$\displaystyle f(x) =\frac{\mathrm{e}^{-6}6^x}{x!}$

para todo ${x\in{\mathbb N}}$ . Determine a probabilidade com que num período específico de 20s mais de oito carros cheguem ao cruzamento. Determine com que probabilidade apenas 2 carros cheguem.

Um piloto deseja segurar seu avião no valor de ${\$200.000}$ . A empresa de seguro estima que uma perda total pode ocorrer com probabilidade ${0,002}$ , uma perda de 50% com probabilidade ${0,01}$ e uma perda de 25% com probabilidade ${0,1}$ . Ignorando as outras perdas parciais, que prêmio a empresa de seguros deveria cobrar a cada ano para ter um lucro de ${\$500}$ ?

Um comprador de transistores os compra em lote de 20 só se a inspeção de 4 deles não apresentar defeito. Um transistor é defeituoso com probabilidade ${0,1}$ de modo independente dos demais. Qual é a proporção de lotes rejeitados?

Há 3 auto-estradas num país. O número de acidentes que ocorrem diariamente nelas é uma v.a. de Poisson com parâmetros ${0,3}$ , ${0,5}$ e ${0,7}$ . Determine o número esperado de acidentes para hoje.

Cada partida que você joga resulta em vitória com probabilidade ${p}$ . Você planeja jogar 5 partidas mas se você vencer a quinta partida então terá que jogar até perder.

Qual é o número esperado de partidas jogadas?

Qual é o número esperado de partidas perdidas?