bc1414 Distribuições Conjunta e Condicionada

Sobre notação: daqui em diante

escrevemos ${P(X\leq k_1,~X\leq k_2,\dots,~X\leq k_j)}$ para denotar ${P\big([X\leq k_1]\cap[X\leq k_2]\cap \cdots\cap [X\leq k_j]\big)}$ .

Se ${X,~Y}$ são v.a. sobre o mesmo espaço amostral, a função de distribuição acumulada conjunta é a função que associa as reais ${a,~b}$ o valor

$\displaystyle F(a,b) \stackrel{\text{\tiny def}}{=} \mathop{\mathbb P}\big( X\leq a,~Y\leq b \big).$

A distribuição de ${X}$ pode ser obtida a partir de ${F}$ do seguinte modo:

$\displaystyle F_X(a) = \mathop{\mathbb P}(X\leq a) = \mathop{\mathbb P}\big(X\leq a , ~ Y<\infty \big).$

Agora, se ${b_1 < b_2}$ então ${[Y\leq b_1] \subset [Y\leq b_2]}$ , portanto

$\displaystyle [X\leq a] \cap [Y\leq b_1] \subset [X\leq a] \cap [Y\leq b_2]$

e fazendo ${E_n = [X\leq a] \cap [Y\leq n]}$ temos uma sequência crescente de eventos logo (veja exercício 25)

$\displaystyle \lim_{n\rightarrow \infty}\mathop{\mathbb P}(E_n) = \mathop{\mathbb P}\left(\bigcup_{n\geq 0}E_n\right)$

ou seja

$\displaystyle \lim_{n\rightarrow \infty} F(a,n) = \mathop{\mathbb P}\big( X\leq a , Y<\infty \big).$

Em resumo,

$F_X(a) = \lim_{b\rightarrow\infty} F(a,b)$ ,
$F_Y(b) = \lim_{a\rightarrow\infty} F(a,b)$ ,

são as distribuições marginais de ${X}$ e ${Y}$ , respectivamente.

Exercício 72 Mostre que

$\displaystyle \mathop{\mathbb P}\big( X>a, ~ Y>b\big) = 1-F_X(a) -F_Y(b)+F(a,b).$

Se ${X}$ e ${Y}$ são v.a. discretas então

$\displaystyle f(a,b) = \mathop{\mathbb P}\big( X=a, ~Y=b \big)$

é a função de massa de probabilidade conjunta, e para tal

${f(a,b)\geq 0}$ ;
$\sum_a\sum_b f(a,b)=1$ ;
$\mathop{\mathbb P}\big( (X,Y)\in A \big) = \sum_{(a,b)\in A}f(a,b)$ , para qualquer conjunto enumerável ${A}$ de pares de valores reais;

as funções de probabilidade marginais de ${X}$ e de ${Y}$ são, respectivamente

$\displaystyle f_X(a) =\sum_b f(a,b) \quad \textrm{ e } \quad f_Y(b) =\sum_a f(a,b).$

Dizemos que ${X}$ e ${Y}$ são v.a. conjuntamente contínuas se existe uma função de densidade de probabilidade conjunta ${f}$ tal que

$\displaystyle F(a,b) = \int_{-\infty}^b \int_{-\infty}^a f(x,y)\,\mathrm{d}x\,\mathrm{d}y$

e para tal ${f}$

${f(x,y)\geq 0}$ ;
$\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty} f(x,y)\,\mathrm{d}x\,\mathrm{d}y=1$ ;
$\mathop{\mathbb P}\big( (X,Y)\in A \big) = \iint\limits_{A}f(x,y)\,\mathrm{d}x\,\mathrm{d}y$ , para qualquer região ${A}$ do plano;

as distribuições marginais de ${X}$ e de ${Y}$ são, respectivamente

$F_X(a) = \lim_{b\rightarrow\infty} F(a,b) = \int_{-\infty}^a \left( \int_{-\infty}^\infty f(x,y)\,\mathrm{d}y\right)\,\mathrm{d}x$ ,
$F_Y(b) = \lim_{a\rightarrow\infty} F(a,b) = \int_{-\infty}^b \left(\int_{-\infty}^\infty f(x,y)\,\mathrm{d}x\right)\,\mathrm{d}y$ ,

e as densidades marginais

$\displaystyle f_X(x) =\int_{-\infty}^{+\infty} f(x,y)\,\mathrm{d}y \quad \textrm{ e } \quad f_Y(y) =\int_{-\infty}^{+\infty} f(x,y)\,\mathrm{d}x.$

Exercício 73 Mostre que

$\displaystyle f(x,y) = \frac{\partial ^2 }{\partial x\partial y}F(x,y)$

quando as derivadas parciais existem.

Exemplo 93 Dois refis de caneta são selecionados ao acaso dentre 3 azuis, 2 vermelhos e 3 verdes. Sejam ${X}$ o número de refis azuis e ${Y}$ o número de refis vermelhos selecionados. A função de probabilidade conjunta é, para ${x,y\in\{0,1,2\}}$ sujeito a condição ${x+y\leq 2}$ ,

$\displaystyle f(x,y) = \frac{\binom 3x \binom 2y \binom 3{2-x-y}} {\binom 82}$

cujos valores está descrito na tabela abaixo

${x\backslash y}$ ${0}$ ${1}$ ${2}$

${0}$ ${3/28}$ ${3/14}$ ${1/28}$

${1}$ ${9/28}$ ${3/14}$ ${0}$

${2}$ ${3/28}$ ${0}$ ${0}$

A probabilidade ${\mathop{\mathbb P}\big( (X,Y) \in \{ (x,y) ~|~ x+y\leq 1\} \big)}$ é ${f(0,0)+f(0,1)+f(1,0) = 9/14}$ .

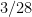
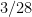
A probabilidade marginal de ${X}$ é dada pela soma da linha da tabela, por exemplo,

$\displaystyle f_X(0) = 3/28 + 3/14 + 1/28.$

Analogamente, a probabiliadade marginal de ${Y}$ é dada pela soma da coluna, por exemplo

$\displaystyle f_Y(1) = 3/14 +3/14 +0.$

Exemplo 94 Um banco resolveu apostar num serviço de drive-thru, além do atendimento convencional. Em um dia ${X}$ é a proporção de tempo que o drive-thru está em uso e ${Y}$ a proporção de tempo que o caixa convencional está em uso, assim ${(X,Y) \in \{(x,y) ~|~ 0\leq x\leq 1,~0\leq y \leq 1\}}$ . Estudos indicam que a função de densidade conjunta é

$\displaystyle f(x,y) = \begin{cases} \frac 65 (x+y^2) & \textrm{ se } 0\leq x\leq 1,~0\leq y \leq 1\\ 0 & \textrm{ caso contr\'ario.} \end{cases}$

A probabilidade de nenhuma das alternativas estar ocupada em mais de um quarto do tempo é ${ \mathop{\mathbb P} \left( 0\leq X\leq \frac 14 , ~ 0 \leq Y \leq \frac 14 \right) }$

$\displaystyle = \int_0^{1/4} \int_0^{1/4} \frac 65 (x+y^2) \,\mathrm{d}x\,\mathrm{d}y = \int_0^{1/4} \int_0^{1/4} \frac 65 x \,\mathrm{d}x\,\mathrm{d}y + \int_0^{1/4} \int_0^{1/4} \frac 65 y^2 \,\mathrm{d}x\,\mathrm{d}y =\frac 7{640}.$

Ademais

$\displaystyle f_X(x) = \int_{-\infty}^{+\infty} \frac 65(x+y)^2\,\mathrm{d}y = \int_{0}^{1} \frac 65(x+y)^2\,\mathrm{d}y = \frac 65x+\frac 25$

é a função de densidade de probabilidade do tempo que o drive-thru está ocupado para ${x\in[0,1]}$ , e ${f_X(x)=0}$ para os outros valores de ${x}$ . Também,

$\displaystyle f_Y(y) = \int_{-\infty}^{+\infty} \frac 65(x+y)^2\,\mathrm{d}x = \int_{0}^{1} \frac 65(x+y)^2\,\mathrm{d}x = \frac 65y^2+\frac 35$

é a função de densidade de probabilidade do tempo que o caixa convencional está ocupado para ${y\in[0,1]}$ e ${f_Y(y)=0}$ para os outros valores de ${y}$ .

Exemplo 95 Sejam ${X}$ e ${Y}$ as coordenadas de um ponto escolhido no círculo de raio ${1}$ e centro na origem de um sistema de coordenadas com densidade conjunta

$\displaystyle f(x,y) = \begin{cases} \frac 1{\pi} &\text{ se } x^2+y^2\leq 1\\ 0 &\text{ se } x^2+y^2> 1\\ \end{cases}$

A densidade marginal de ${X}$ é

$\displaystyle f_X(x) = \int_{-\infty}^{+\infty} f(x,y)\, \mathrm{d}y = \int_{-\sqrt{1-x^2}}^{+\sqrt{1-x^2}} \frac{1}{\pi}\, \mathrm{d}y = \frac 2{\pi} \sqrt{1-x^2} \qquad (\forall x, ~x^2 \leq 1),$

e ${f_X(x)=0}$ nos outros casos. Analogamente,

$\displaystyle f_Y(y)= \frac 2{\pi}\sqrt{1-y^2} \qquad (\forall y, ~ y^2 \leq 1)$

e ${f_Y(y)=0}$ nos outros casos.

A distância do ponto escolhido para a origem é a v.a. ${D=\sqrt{X^2+Y^2}}$ cuja distribuição é, para ${a\in [0,1]}$ , dada por ${F_D(a) = \mathop{\mathbb P}\big( \sqrt{X^2+Y^2} \leq a \big)= }$

$\displaystyle = \iint\limits_Af(x,y)\,\mathrm{d}x\,\mathrm{d}y = \iint\limits_A\frac 1\pi\,\mathrm{d}x\,\mathrm{d}y = \frac 1\pi \iint\limits_A\,\mathrm{d}x\,\mathrm{d}y = \frac 1\pi \pi a^2 = a^2, \qquad A = \{(x,y)\colon x^2+y^2 \leq a^2\}.$

A função de densidade de ${D}$ é ${f_D(a)= \frac 2a}$ para ${a\in [0,1]}$ , portanto

$\displaystyle \mathop{\mathbb E}(D) = \int_{-\infty}^{+\infty} af_D(a)\,\mathrm{d}a = \int_{0}^{1} 2a^2\,\mathrm{d}a = \frac 23.$

Variáveis aleatórias independentes Dizemos que as v.a. ${X}$ e ${Y}$ são independentes se para quaisquer conjuntos ${A}$ e ${B}$ de números reais vale

$\displaystyle \mathop{\mathbb P} \big( [X\in A] \cap [Y\in B] \big) = \mathop{\mathbb P} \big( X\in A \big) \mathop{\mathbb P}\big(Y\in B \big). \ \ \ \ \ (39)$

Isso equivale a dizer que para quaisquer ${a,b\in{\mathbb R}}$

$\displaystyle \mathop{\mathbb P} \big( [X\leq a] \cap [Y\leq b] \big) = \mathop{\mathbb P} \big( X\leq a \big) \mathop{\mathbb P}\big(Y\leq b \big). \ \ \ \ \ (40)$

como estabelece o seguinte exercício.

Exercício 74 (Independência de v.a. conjuntamente distribuídas) Prove que ${X}$ e ${Y}$ são v.a. independentes, com distribuição conjunta ${F(x,y)}$ se e só se

$\displaystyle F(x,y) = F_X(x) F_Y(y). \ \ \ \ \ (41)$

Decorre daí que ${X}$ e ${Y}$ independentes é suficiente

$\displaystyle f(x,y) = f_X(x)f_Y(y)$

para quaisquer reais ${x}$ e ${y}$ .

Exemplo 96 Se

$\displaystyle f(x,y)= \begin{cases} 24xy, & \text{ se }x\in[0,1],~y\in [0,1],~x+y\leq 1\\ 0, & \text{ caso contr\'ario.} \end{cases}$

é a distribuição conjunta de ${X}$ e ${Y}$ então ${f_X(3/4) = f_Y(3/4) = 9/{16}}$ e ${f(3/4,3/4)=0}$ portanto

$\displaystyle f_X(x)f_Y(y) \neq f(x,y)$

ou seja, embora ${f(x,y) = g(x)h(y)}$ as funções ${g}$ e ${h}$ não podem ser feitas distribuições marginais.

Exercício 75 Prove que se ${f(x,y) = g(x)h(y)}$ para todo ${x\in {\mathbb R}}$ e todo ${y\in R}$ (no exemplo acima isso não vale pois as variáveis são relacionadas na região onde ${f}$ é não-nula) então ${X}$ e ${Y}$ são independentes.

Exemplo 97 (O problema da agulha de Buffon) Suponha que temos um piso feito de tábuas paralelas de madeira, cada uma da mesma largura ${t\,\mathrm{cm}}$ , e nós deixamos cair uma agulha de comprimento ${\ell \,\mathrm{cm}}$ no chão, ${\ell < t}$ . Qual é a probabilidade de que a agulha irá cruzar a divisória onde duas tábuas se encontram?

Seja ${\theta\in [0,\pi/2]}$ o ângulo (agudo) com que a agulha cai em relação à vertical que passa pela centro da agulha. Seja ${r\in [0,t/2]}$ a distância do centro da agulha até a divisória entre tábuas mais próxima. Assumimos que ${r}$ e ${\theta}$ são variáveis aleatórias independentes e uniformemente distribuídas.

Se ${r < \frac {\ell}2 \sin(\theta)}$ então a agulha cruzou uma das divisórias e a probabilidade desse evento é

$\displaystyle \mathop{\mathbb P} \left(r < \frac {\ell}2 \sin(\theta) \right) = \iint\limits_{\big\{(x,y)\colon x< \frac {\ell}2 \sin (y)\big\}} f_r(x)f_\theta(y)\,\mathrm{d}x\,\mathrm{d}y=$

$\displaystyle = \int_{0}^{\pi/2}\int_{0}^{\frac {\ell}2 \sin (y)} \frac 2\pi \frac 2t \,\mathrm{d}x\,\mathrm{d}y = \frac 4{\pi t} \int_{0}^{\pi/2} \frac {\ell}2 \sin (y)\,\mathrm{d}y = \frac 4{\pi t} \frac {\ell}2 \int_{0}^{\pi/2} \frac {\ell}2 \sin (y)\,\mathrm{d}y =\frac{2{\ell}}{\pi t}.$

Veja aqui uma simulação usada para determinar o valor aproximado de ${\pi}$ .

Usando R:

podemos estimar $\pi$ com a função

estPi<- function(n, l=1, t=2) {
 m <- 0
 for (i in 1:n) {
 x <- runif(1)
 theta <- runif(1, min=0, max=pi/2)
 if (x < l/2 * sin(theta)) {
 m <- m +1
 }
 }
 return(2*l*n/(t*m))
}

e vizualizar uma simulação com

L=0.35 #meia agulha
D=20   #tamanho do quadro
N=10^3 #numero de lancamentos


#N pontos (R,T) 
R=runif(N,min=L,max=D-L)   #posicao vertical centro
C=cbind(runif(N,0,D),R)	   #coordenadas (x,y) do centro no plano
T=runif(N,min=0,max=pi)    #angulo anti-horario

#extremos das agulhas
A=C+L*cbind(cos(T),sin(T)) 
B=C-L*cbind(cos(T),sin(T)) 

#numero de cruzamentos
numbhits=function(A,B){
 sum(abs(trunc(A[,2])-trunc(B[,2]))>0)}

plot(C,type="n",axes=F,xlim=c(0,D),ylim=c(0,D))

#linhas do piso
for (i in 1:(D-1))
 abline(h=i,lty=2,col="sienna")

#desenho das agulhas
for (t in 1:N)
 lines(c(A[t,1],B[t,1]),c(A[t,2],B[t,2]),col="steelblue")

title(main=paste(numbhits(A,B),"cruzamentos",sep=" "))

Observação 5 Esses conceitos desenvolvidos até aqui podem ser estendidos, de modo natural, ao caso de 3 ou mais v.a..

Exemplo 98 Sejam ${X, ~Y,~Z}$ v.a. independentes e uniformemente distribuídas sobre ${[0,1]}$ . Então

$\displaystyle \mathop{\mathbb P}( X \geq YZ) = \iiint\limits_{\big\{(x,y,z)\colon x\geq yz\big\}} f_{X,Y,Z}(x,y,z)\,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z$

$\displaystyle = \int_0^1 \int_0^1 \int_{yz}^1 \,\mathrm{d}x\,\mathrm{d}y\,\mathrm{d}z =\int_0^1 \int_0^1 (1-yz) \,\mathrm{d}y\,\mathrm{d}z = \int_0^1 \left(1-\frac z2\right)\,\mathrm{d}z = \frac 34.$

Exercício 76 Mostre que se ${X}$ e ${Y}$ são v.a. independentes então

$\displaystyle F_{X+Y}(a) = \int_{-\infty}^{+\infty} F_X(a-y)f_Y(y)dy \quad\;\textrm{ e }\quad\; f_{X+Y}(a) = \int_{-\infty}^{+\infty} f_X(a-y)f_Y(y)dy .$

Se ${X}$ e ${Y}$ têm distribuição conjunta ${f(x,y)}$ e ${h}$ é uma função a duas variáveis reais, então o valor médio de ${h(X,Y)}$ é

$\displaystyle \mathop{\mathbb E}(h(X,Y)) = \begin{cases} \displaystyle \sum_x\sum_y h(x,y)f(x,y) \\ \displaystyle \int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty} h(x,y)f(x,y)\,\mathrm{d}x\,\mathrm{d}y \end{cases}$

nos casos discreto e contínuo, respectivamente.

Exercício 77 O que é ${\mathop{\mathbb E}(h(X,Y))}$ no caso ${h(X,Y)=X}$ ?

Notemos que se ${X}$ e ${Y}$ são independentes então ${\mathop{\mathbb E}\big(g(X)h(Y)\big) = \mathop{\mathbb E}\big(g(X)\big)\mathop{\mathbb E}\big(h(Y)\big)}$ , pra quaisquer funções ${g,~h}$ . De fato

$\displaystyle \begin{array}{rcl} \mathop{\mathbb E}\big(g(X)h(Y)\big) &=& \displaystyle \int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty} g(x)h(y)f(x,y)\,\mathrm{d}x\,\mathrm{d}y \\ &=& \displaystyle \int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty} g(x)h(y)f_X(x)f_Y(y)\,\mathrm{d}x\,\mathrm{d}y \\ &=& \displaystyle \int_{-\infty}^{+\infty} g(x)f_X(x)\,\mathrm{d}x \int_{-\infty}^{+\infty} h(y)f_Y(y)\,\mathrm{d}y \\ &=&\mathop{\mathbb E}\big(g(X)\big)\mathop{\mathbb E}\big(h(Y)\big). \end{array}$

Dedução análoga vale para distribuição conjunta discreta. Em particular, se ${X}$ e ${Y}$ são independentes então

$\displaystyle \mathop{\mathbb E}(XY)=\mathop{\mathbb E}(X)\mathop{\mathbb E}(Y). \ \ \ \ \ (42)$

Exercício 78 Ache exemplos de v.a. que satisfazem (42) mas que não são independentes.

— Covariância —

A covariância entre as variáveis ${X}$ , ${Y}$ é definida por

$\displaystyle \begin{array}{rcl} \mathrm{Cov}(X,Y) &\stackrel{\text{\tiny def}}{=}& \mathop{\mathbb E}\big( (X-\mathop{\mathbb E}(X))(Y-\mathop{\mathbb E}(Y))\big)\\ &=& \mathop{\mathbb E}(XY)-\mathop{\mathbb E}(X)\mathop{\mathbb E}(Y). \end{array}$

a segunda igualdade segue por linearidade da esperança.

Quando ${X}$ e ${Y}$ são independentes, por (42), temos ${\mathrm{Cov}(X,Y) = 0}$ . A recíproca não é verdadeira, se ${\mathrm{Cov}(X,Y) = 0}$ não necessariamente as v.a. são independentes, pode significar que as v.a. são de alguma forma relacionadas.

Exemplo 99 Se ${X}$ assume cada um dos valores ${-1}$ , ${0}$ e ${1}$ com probabilidade ${1/3}$ e ${Y}$ é a variável indicadora do evento ${X=0}$ , então ${\mathrm{Cov}(X,Y)=0}$ (verifique), entretanto não são variáveis independentes (verifique).

Exemplo 100 Sejam ${I_A}$ e ${I_B}$ v.a. indicadoras de ocorrência dos eventos ${A}$ e ${B}$ , respectivamente

$\displaystyle \mathrm{Cov}(I_A,I_B) = \mathop{\mathbb P}\big( I_A\cap I_B \big) - \mathop{\mathbb P}\big(I_A\big)\mathop{\mathbb P}\big(I_B\big) = \mathop{\mathbb P}\big( A\cap B \big) - \mathop{\mathbb P}\big(A\big)\mathop{\mathbb P}\big(B\big) = \mathop{\mathbb P}(B)\big( \mathop{\mathbb P}\big(A~|~B ) - \mathop{\mathbb P}\big(A\big)\big)$

portanto, ${\mathrm{Cov}(I_A,I_B) >0}$ se e só se ${\mathop{\mathbb P}\big( A~|~B \big) > \mathop{\mathbb P}(A)}$ , ou seja, o evento ${B}$ faz ser mais provável ${A}$ (e vice-versa).

A covariância satisfaz as seguintes propriedades, cuja verificação fica como exercício.

${\mathrm{Cov}(X,X) = \mathrm{Var}(X)}$ ;
${\mathrm{Cov}(X,Y) = \mathrm{Cov}(Y,X)}$ ;
${\mathrm{Cov}(cX,Y) = c\mathrm{Cov}(X,Y)}$ para qualquer constante ${c}$ ;
$\mathrm{Cov}(\sum_{i=1}^nX_i,\sum_{j=1}^m Y_j)= \sum_{i=1}^n\sum_{j=1}^m \mathrm{Cov}(X_i,Y_j)$ .

Exercício 79 Prove as propriedades.

Exercício 80 Prove que ${\mathrm{Cov}(X,Y) = \pm \mathrm{Var}(X)\mathrm{Var}(Y)}$ se e só se ${Y=aX+b}$ para ${a\neq 0}$ e ${b}$ reais.

Das propriedades acima, conseguimos deduzir que

$\displaystyle \mathrm{Var} \left( \sum_{i=1}^nX_i \right) = \mathrm{Cov}\left(\sum_{i=1}^nX_i , \sum_{i=j}^nX_j \right) = \sum_{i=1}^n \mathrm{Var}(X_i) +\sum_{i=1}^n\sum_{\substack{j=1\\j\neq i}}^n \mathrm{Cov}(X_i,X_j).$

Por conseguinte, se a soma é de v.a. independentes então

$\displaystyle \mathrm{Var} \left( \sum_{i=1}^nX_i \right) = \sum_{i=1}^n \mathrm{Var} \left( X_i \right).$

Exercício 81 Use a identidade acima para obter a variância de ${X\sim \mathrm{Binomial}(n,p)}$ .

— Distribuição e esperança condicionais —

Se ${X}$ e ${Y}$ são v.a. discretas e ${x\in{\mathbb R}}$ é tal que e ${f_X(x) > 0}$ então a distribuição condicional de ${Y}$ dado ${X=x}$ é a função em ${y\in{\mathbb R}}$ dada por

$\displaystyle F(y~|x) \stackrel{\text{\tiny def}}{=} \mathop{\mathbb P}(Y\leq y ~|~X=x) \ \ \ \ \ (43)$

a função (de massa/de densidade) de probabilidade condicional de ${Y}$ dado que ${X=x}$ é

$\displaystyle f(y~|x) \stackrel{\text{\tiny def}}{=} \frac{f(x,y)}{f_X(x)}.$

Notemos que no caso discreto

$\displaystyle \mathop{\mathbb P} \big( Y=y ~|~ X=x \big) = \frac{\mathop{\mathbb P} \big( Y=y, ~X=x \big)}{\mathop{\mathbb P}(X=x)} = \frac{f(x,y)}{f_X(x)}$

para qualquer valor real ${y}$ . A última fração é uma função de ${y}$ , com ${x}$ fixo e satisfaz as condições de função de massa de probabilidade.

Notemos também que, caso as v.a. sejam independentes vale ${f(y~|x) = f_Y(y)}$ e vice-versa, i.e., a igualdade implica independência.

Considerações análogas levam à definição de ${f(x~|y)}$ . Naturalmente,

$\displaystyle \mathop{\mathbb E} \big( Y~|~X=x \big) = \begin{cases} \displaystyle\sum_y y f(y~|x) & \textrm{ no caso discreto}\\ \displaystyle\int_{-\infty}^{+\infty} y f(y~|x)\,\mathrm{d} y & \textrm{ no caso cont\'inuo.} \end{cases} \ \ \ \ \ (44)$

Notemos que quando as v.a. são independentes ${\mathop{\mathbb E} \big( Y~|~X=x \big) = \mathop{\mathbb E}(Y)}$ (verifique).

Se ${\mu(x) \stackrel{\text{\tiny def}}{=} \mathop{\mathbb E} \big( Y~|~X=x \big)}$ então ${\mu(X)}$ é a esperança condicional de ${Y}$ dado ${X}$ , denotada

$\displaystyle \mathop{\mathbb E} \big( Y~|~X \big)$

que embora sugira uma média é, de fato, uma variável aleatória, a qual tem a seguinte propriedade

Exercício 82 $\mathop{\mathbb E} \Big( \mathop{\mathbb E} \big( Y~|~X\big) \Big) = \mathop{\mathbb E}(Y).$

Logo

$\displaystyle \mathop{\mathbb E} \big( Y \big) = \begin{cases} \displaystyle\sum_x \mathop{\mathbb E}(Y~|~X=x)\mathop{\mathbb P}(X=x) & \textrm{ no caso discreto}\\ \displaystyle\int_{-\infty}^{+\infty} \mathop{\mathbb E}(Y~|~X=x) f_X(x)\,\mathrm{d} x & \textrm{ no caso cont\'inuo.} \end{cases} \ \ \ \ \ (45)$

Exemplo 101 De volta ao exemplo 94, a distribuição de ${Y}$ condicionada a ${X=8}$ é

$\displaystyle f(y~|~0,8) = \frac{f(0,8,y)}{f_X(0,8)} = \frac{1,2(0,8+y^2)}{1,2\cdot 0,8 +0,4}, \quad \forall y\in (0,1)$

A probabilidade do caixa convencional estar ocupado metade do tempo, dado que ${X=8}$ , é

$\displaystyle \mathop{\mathbb P}(Y\leq 0,5~|~X=8) = \int_{-\infty}^{0,5} f(y~|~0,8)\,\mathrm{d}y = 0,39.$

Usando a distribuição marginal temos que ${\mathop{\mathbb P}(Y\leq 0,5)=0,35}$ . Ademais ${\mathop{\mathbb E}(Y)= 6}$ e

$\displaystyle \mathop{\mathbb E}(Y~|~X=8) = \int_{-\infty}^{+\infty} y f(y~|~0,8)\,\mathrm{d}y = 0,574.$

Exemplo 102 Sejam ${X,~Y\sim\mathrm{Binomial}(n,p)}$ independentes. Então

$\displaystyle \mathop{\mathbb P} (X+Y = m) = \sum_{i=0}^n \mathop{\mathbb P}(X=i,~Y=m-i) = \sum_{i=0}^n \mathop{\mathbb P}(X=i)\mathop{\mathbb P}(Y=m-i)$

$\displaystyle = \sum_{i=0}^n \binom ni \binom n{m-i} p^m(1-p)^{n-m+n} = \binom {2n}m p^m(1-p)^{2n-m}$

pois ${\binom {a+b}k = \sum_{i=0}^n \binom ai \binom b{k-i}}$ . Desse fato temos

$\displaystyle \begin{array}{rcl} \mathop{\mathbb P}(X=k~|~X+Y=m) &=& \frac{\mathop{\mathbb P}(X=k \,,\, X+Y=m)}{ \mathop{\mathbb P}(X+Y=m)}\\ \displaystyle&=& \frac{\mathop{\mathbb P}(X=k \,,\, Y=m-k)}{ \mathop{\mathbb P}(X+Y=m)}\\ \displaystyle&=& \frac{\mathop{\mathbb P}(X=k)\mathop{\mathbb P}(Y=m-k)}{ \mathop{\mathbb P}(X+Y=m)}\\ \displaystyle&=& \frac{\binom nk p^k(1-p)^{n-k}\binom n{m-k}p^{m-k}(1-p)^{n-m+k}} {\binom{2n}m p^m(1-p)^{2n-m}} \\ &=& \frac{\binom nk\binom n{m-k}}{\binom{2n}m} \end{array}$

ou seja, ${X}$ condicionada a ${X+Y=m}$ tem distribuição hipergeométrica com parâmetros ${2n,n,m}$ , logo

$\displaystyle \mathop{\mathbb E}(X ~|~X+Y=m) = \frac m2.$

Exemplo 103 (Esperança de v.a. geométrica) Seja ${X}$ o número de lançamentos de uma moeda até sair cara, o que ocorre com probabilidade ${p}$ , seja ${Y}$ a v.a. indicadora de “cara no primeiro lançamento”. Assim,

$\displaystyle \mathop{\mathbb E}(X) = \mathop{\mathbb E}(\mathop{\mathbb E}(X|Y)) = \mathop{\mathbb E}(X~|~Y=0)(1-p) +\mathop{\mathbb E}(X~|~Y=1)p$

mas ${\mathop{\mathbb E}(X~|~Y=1) =1}$ e~ ${\mathop{\mathbb E}(X~|~Y=0) = \mathop{\mathbb E}(X+1)}$ , portanto

$\displaystyle \mathop{\mathbb E}(X) = \mathop{\mathbb E}(X)(1-p) + (1-p) + p$

que resolvendo para ${\mathop{\mathbb E}(X)}$ resulta em ${\mathop{\mathbb E}(X)=1/p}$ , como já sabíamos. Do mesmo modo, temos

$\displaystyle \mathop{\mathbb E}(X^2) = \mathop{\mathbb E}(X^2~|~Y=0)(1-p) +\mathop{\mathbb E}(X^2~|~Y=1)p = \mathop{\mathbb E}(X+1)^2(1-p) +p$

que resolvendo para ${\mathop{\mathbb E}(X^2) }$ resulta em

$\displaystyle \mathop{\mathbb E}(X^2) = \frac{2-p}p^2$

e com isso

$\displaystyle \mathrm{Var}(X) = \mathop{\mathbb E}(X^2) -\mathop{\mathbb E}(X)^2= \frac{2-p}p^2 - \frac 1p^2 = \frac{1-p}p^2.$

Exemplo 104 (Soma de v.a. com número aleatório de termos) Num determinado dia do cotidiano de uma loja ${N}$ pessoas entram na loja, com ${\mathop{\mathbb E}(N)=50}$ , e o gasto dessa pessoas são dados pelas v.a. independentes ${X_1,X_2,\dots,X_N}$ com ${\mathop{\mathbb E}(X_i)=\mu =80}$ reais, para todo ${i}$ , e independentes de ${N}$ .

A quantia gasta num determinado dia é ${X = \sum_{i=1}^N X_i}$ cuja média é

$\displaystyle \mathop{\mathbb E} \left( X \right) = \mathop{\mathbb E} \big( \mathop{\mathbb E}(X~|~N) \big) =\mathop{\mathbb E} \left( \mathop{\mathbb E}\left( \sum_{i=1}^N X_i~\Bigg|~N\right) \right)$

Agora,

$\displaystyle \mathop{\mathbb E}\left( \sum_{i=1}^n X_i~\Bigg|~N=n \right) = \mathop{\mathbb E}\left( \sum_{i=1}^n X_i \right) =n\mu$

por causa da independência, por fim

$\displaystyle \mathop{\mathbb E}\left( \mathop{\mathbb E}\left( \sum_{i=1}^N X_i ~\Bigg|~N \right) \right) = \mathop{\mathbb E}\big( N\mu \big) = \mathop{\mathbb E}(N)\mu = 4.000$

reais.

Exercício 83 Considere o espaço amostral das sequências definidas pelas permutações de ${\{1,2,3\}}$

$\displaystyle \Omega = \{(1,2,3),(1,3,2),(2,1,3),(2,3,1),(3,1,2),(3,2,1),(1,1,1),(2,2,2),(3,3,3)\}.$

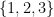
Seja ${X_i(\omega)}$ a ${i}$ -ésima coordenada de ${\omega}$ , para ${i=1,2,3}$ . Defina ${N}$ a variável aleatória igual a ${X_2}$ . Prove que

para todo ${i,j\in\{1,2,3\}}$ , vale ${\mathop{\mathbb P} (X_i=j)=1/3}$ ;
as variáveis ${X_i}$ não são independentes;
${\displaystyle\sum_{i=1}^{\mathop{\mathbb E} N}\mathop{\mathbb E} X_i = 4}$ e conclua que
$\displaystyle \mathop{\mathbb E} \left(\sum_{i=1}^{ N} X_i \right) \neq \sum_{i=1}^{\mathop{\mathbb E} N}\mathop{\mathbb E} X_i.$

Exemplo 105 Sejam ${U_1,U_2,\dots}$ v.a. com distribuição ${\mathrm{Uniforme}((0,1))}$ independentes e ${m(x)}$ o valor esperado para ${N(x)}$ que é o menor ${n}$ para o qual ${U_1+\cdots +U_n >x}$ . Certamente,

$\displaystyle \mathop{\mathbb E}\big( N(x)~|~U_1=y\big) = \begin{cases} 1, &\textrm{ se } y>x\\ 1+ m(x-y), &\textrm{ se } y\leq x. \end{cases}$

Portanto,

$\displaystyle m(x) = \int_0^1 \mathop{\mathbb E}(N(x)~|~U_1=y)\,\mathrm{d}y = 1+ \int_0^x m(x-y)\,\mathrm{d}y = 1 + \int_0^x m(u)\,\mathrm{d}u.$

Derivando os extremos dessa cadeia de igualdades obtemos ${m'(x) = m(x)}$ , ou seja, ${m(x) = a\mathrm{e}^x}$ para alguma constante real ${a}$ e como ${m(0)=1}$ temos

$\displaystyle m(x) = \mathrm{e}^x$

é o número esperado de termos para que a soma de v.a. uniformes em ${(0,1)}$ ultrapasse o valor ${x}$ .

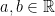
Exercício 84 Mostre que para constantes ${a,b\in{\mathbb R}}$

$\displaystyle \mathop{\mathbb E}(aX+bY~|~Z) = a\mathop{\mathbb E}(X~|~Z)+ b\mathop{\mathbb E}(Y~|~Z).$

Exercício 85 Mostre que ${\mu(X) = \mathop{\mathbb E}(Y~|~X)}$ satisfaz

$\displaystyle \mathop{\mathbb E}(\mu(X)g(X)) = \mathop{\mathbb E}(Yg(X))$

para qualquer função ${g}$ pra qual as esperanças acima existam.

Exercício 86 Uma galinha bota ${N}$ ovos, em que ${N\sim \mathrm{Poisson}(\lambda)}$ . Cada ovo vinga com probabilidade ${p}$ e independente dos outros ovos. Calcule ${\mathop{\mathbb E}(N~|~K)}$ , ${\mathop{\mathbb E}(K)}$ e ${\mathop{\mathbb E}(K~|~N)}$ , em que ${K}$ é o número de pintinhos.