bc1414 Cadeias de Markov

Uma coleção de variáveis aleatórias que assumem valor num conjunto de estados é um processo estocástico. O índice é interpretado como tempo e o valor de é o estado do processo no instante . O processo é dito de tempo-discreto ou tempo-contínuo dependendo de ser enumerável ou não, respectivamente. Cadeias de Markov são um caso particular de processo estocástico de tempo discreto e variávaeis discretas. No que segue fixamos e a menos que seja dito o contrário . Nessas condições um processo estocástico é uma cadeia de Markov se vale a condição de Markov de que o estado futuro depende somente do estado atual e é independente dos estados passados

e ela é dita homogênea se essa probabilidade não depende do tempo , que é o caso que estudaremos a seguir.

Chamamos de estado inicial e sua distribuição de distribuição inicial.

Uma cadeia de Markov é caracterizada por

1. conjuntos de estados ,
2. distribuição inicial , de modo que ,
3. probabilidades de transição do estado para o estado , para todo ,

   

de modo que uma sequência de v.a. com valores em é uma cadeia de Markov homogênea com distribuição inicial e probabilidade transição se a distribuição conjunta de , para todo , é

para toda escolha de . Dessa distribuição conjunta temos

e

que é a condição de Markov (46). Ademais , fixado , temos a partir dos itens 2 e 3 acima que

portanto 47 é uma atribuição de probabilidades válida no espaço das realizações das variáveis. A mesma dedução vale para qualquer valor de portanto a definição da distribuição é consistente (o Teorema de Kolmogorov garante a existência das variáveis).

Exercício 87 Prove que o evento

ocorre com mesma probabilidade em todo espaço das realizações das variáveis com pelo menos variáveis.

Como todas as cadeias desse capítulo são homogêneas nós omitiremos esse adjetivo daqui em diante.

Convencionamos que quando é dada uma definição de uma cadeia de Markov, as probabilidades de transição que não são dadas explicitamente são iguais a zero. Ademais, usualmente não damos a distribuição inicial porque ou esse parâmetro não é relevante ou é trivial (i.e., para algum ).

A seguir daremos alguns exemplos de cadeias de Markov.

Exemplo 106 Numa pilha com cartas de baralho distintas numeradas de a , definimos uma cadeia de Markov tomando um estado para cada permutação , em que é a posição da -ésima carta; é a permutação identidade com probabilidade .

Uma transição entre estados é obtida retirando a carta topo e colocando-á numa posição arbitrária escolhida uniformemente entre as cartas restantes na pilha, logo

para todo e com a permutação obtida a partir da permutação pelo processo descrito acima (nos casos em que não pode ser obtida pelo processo descrito vale , como convencionamos). Um problema interessante é estimar o valor , caso exista, para o qual a distribuição de seja aproximadamente uniforme.

Exemplo 107 Sejam variáveis aleatórias independentes, e para , tomemos . Então

enquanto que

logo não é uma cadeia de Markov por não satisfazer (46).

Exemplo 108 Definimos uma cadeia de Markov se tomamos o conjunto de estados como sendo os inteiros positivos, , o estado inicial com probabilidade e as transições probabilidades

para todo inteiro .

Exemplo 109 (passeio aleatório) Tomemos o conjunto de estados como os inteiros, , o estado inicial com probabilidade e as transições de estados têm as probabilidades

para todo inteiro e algum . Essa cadeia é um passeio aleatório pelos inteiros.

Exemplo 110 Seja um grafo finito. Definimos uma cadeia de Markov tomando como o conjunto de vértices do grafo e as transições são definidas de modo que se então é qualquer vértice adjacente a com probabilidade uniforme. Esse tipo de cadeia de Markov é conhecida como passeio aleatório num grafo.

Exemplo 111 (Cadeia de Markov não-homogênea) Suponha v.a. independentes e identicamente distribuídas com

para todo . Agora, tomemos para todo .

A sequência de v.a. não define uma cadeia de Markov pois

enquanto que

No entanto, é uma cadeia de Markov não homogênea pois, por exemplo

Exemplo 112 (Cadeia de Markov não-homogênea) Consideremos uma caixa com bolas vermelhas e bolas azuis e o processo de retirar aleatoriamente uma bola da caixa sem reposição. Seja o número de bolas vermelhas na caixa na -ésima rodada. A probabliade de transição não depende só do número de bolas vermelhas (estado), mas também depende do momento .

Exemplo 113 (ruína do jogador) Em um jogo, o jogador ganha 1 real com probabilidade , ou perde 1 real com probabilidade , de modo independente a cada rodada de até que sua fortuna seja ou , nesse momento ele pára de jogar.

Denotamos a quantia do jogador no instante pela variável e temos que

para , são as transições de estado de uma cadeia de Markov.

Um problema interessante para o jogador é conhecer a probabilidade de chegar ao estado antes do estado , esse é um problema clássico da probabilidade conhecido como o problema da ruína do jogador.

Seja a probabilidade de o jogador chegar antes ao estado dado que . Então

para todo , que equivale a

para todo . Para facilitar usaremos Segue da igualdade acima que

donde concluímos, usando que , que

para todo . Iterando

e de temos

Se então a soma acima é de uma progresão geométrica cuja valor é logo

e substituindo em (48)

Notemos que a probabilidade do jogador ficar “infinitamente rico”, i.e., quando , é se pois tendem a . Por outro lado, se então quando logo .

Usando R:

simulaRuina=function(n=10,p=1/2,estado=5)
{
  cat(estado)
  m<-0
  while ( estado < n & estado > 0) {
    proxEstado <- estado + sample(x=c(-1,1), size=1, prob=c(1-p,p))
    cat(" -> ",proxEstado)
    m <- m+1
    estado <- proxEstado 
  }
  cat("\n",m," passos","\n")
}

simulaRuina()

simulaRuina(10,1/3,3)

simulaRuina() simula transições aleatórias até atingir o estado 10 ou 0 a partir do 5 com probabilidade de ganho 1/2;

simulaRuina(10,1/3,3) simula até atingir o estado 10 ou 0 a partir do 3 com probabilidade de ganho 1/3;

também devolve o número de passos esfetuados.

Exemplo 114 Consideremos a cadeia de Markov sobre com estado inicial e as transições de estados têm as probabilidades

para todo inteiro . Vamos estimar o número esperado de passos até a cadeia chegar ao estado . Seja o número de passos para atingir a partir de . Se o estado atual é e o próximo então , senão , portanto, por (45)

e temos

cuja solução é (verifique). Finalmente, . Pela desigualdade de Markov, equação (24), a probabilidade da cadeia não chegar no estado em passos é

e, analogamente, tende a zero a probabilidade da cadeia não chegar no estado em passos qualquer que seja que tenda ao infinito com , por exemplo, .

Usando R:

simulaMCN = function (n , estado =0)
{
  cat ( estado )
  m <-0
  
  while ( estado < n ) {
    
    if ( estado > 0) {
      proxEstado <- estado + sample (x=c ( -1 ,1) , size =1 , prob =c (1 / 2 ,1 / 2) )}
    else { proxEstado <- 1 }
    cat (" -> " , proxEstado )
    
    m <- m +1
    estado <- proxEstado
  }
  cat ("\ n" ,m ," passos " ," \n")
}

simulaMCN(10) simula até atingir o estado 10 a partir do 0;

simulaMCN(10,3) simula até atingir o estado 10 a partir do 3;

também devolve o número de passos esfetuados.

Exemplo 115 Suponha que a ocorrência de chuva num dia é determinada pela condição do clima nos dois dias anteriores do seguinte modo: amanhã chove com probabilidade se chove nos dois dias anteriores; amanhã chove com probabilidade se chove hoje mas não choveu ontem; amanhã chove com probabilidade se não chove hoje mas choveu ontem; amanhã chove com probabilidade se não chove nos dois dias anteriores.

Identificamos cada uma das quatro situações acima com seguintes estados se choveu hoje e ontem; se choveu hoje mas não choveu ontem; se não choveu hoje mas choveu ontem; e se não choveu nem hoje e nem ontem.

O estado no dia depende da condição nos dias anteriores; assim a transição de para , por exemplo, ocorre quando não chove amanhã () mas choveu hoje, dado que choveu hoje () e ontem (, nessa configuração a probabilidade de não-chuva amanhã se choveu hoje e ontem é . O seguinte diagrama ilustra as transições de estados com suas probabilidades.

Exercício 88 Um dado é lançado repetidamente. Quais das seguintes sequências de variáveis formam um cadeia de Markov?

1. é o maior resultado até a -ésima rodada;
2. é a quantidade de em rodadas;
3. no instante , é o tempo desde o mais recente;
4. no instante , é o tempo até o próximo .

Exercício 89 Se é uma cadeia de Markov, quais das seguintes sequências é uma cadeia de markov?

1. , para fixo;
2. ;
3. .

Exercício 90 (Equação de Wald e ruína do jogador) Sejam v.a. independentes, identicamente distribuídas, e com esperança finita. Chamamos a v.a. de tempo de parada para a sequência se o evento é independente de para , para todo .

Prove que se tem esperança finita, então

No exemplo 113, seja o estado inicial o tempo de duração do jogo, ou seja, o tempo esperado até a cadeia atingir o estado ou o estado . Assuma que as esperanças sejam finitas e use a equação (50) para determinar .

— Representação matricial, transiência e recorrência —

A matriz definida pelas probabilidades de transição é dita matriz de transições da cadeia de Markov. Ainda, para , se

é a transição do estado para o estado em passos então

para todo inteiro e com e convencionamos . Logo a -ésima potência da matriz é

Notemos que , para qualquer . Uma matriz cujas entradas são não-negativas e as linhas somam é uma matriz estocástica.

Exercício 91 Verifique que se é estocástica então também é estocástica.

Notemos que e usando esse fato podemos deduzir

portanto, vale a seguinte identidade que é bastante útil.

Lema 17 (Identidade de Chapman–Kolmogorov) Se é uma matriz de transição,

para quaisquer , ou ainda, .

A evolução da cadeia é determinada pela matriz e boa parte dos estudos das cadeias de Markov são reduzidas ao estudo das propriedades algébricas desses elementos.

Exemplo 116 No caso do exemplo 115 dado que choveu na segunda-feira e na terça-feira, qual é a probabilidade de chover na quinta?

A matriz toda está descrita abaixo

A matriz de transição em 2 passos é a matriz

e chover na quinta equivale ao processo estar no estado ou no estado , logo a probabilidade é .

Usando R:

#Algoritmo para simulacao de cadeia de Markov nos primeiros N passos,
# daodo M[,]  matriz de transicoes
#
#1. Escolha um estado inicial X0 = j de arcordo com a distribuicao inicial.
#2. i <- 1
#3. Repita N vezes
#4.    Gerar Y_j  com distribuicao M[j,]
#5.    Xi <- Yj,
#6.     j <- Xi
#7.     i <- i+1

simulaMC=function(N=100)
{
  # matriz transicao
  trans = matrix(c( 
    0.7,0,0.3,0,
    0.5,0,0.5,0,
    0,0.4,0,0.6,
    0,0.2,0,0.8
    ), ncol=4, byrow=TRUE);

  # estado inicial
  estado =  sample(x=1:ncol(trans), size=1, prob=c(1/4,1/4,1/4,1/4))
  cat(estado)
  
  # N passos da cadeia
  for (i in 1:N) {

    proxEstado <- sample(x=1:ncol(trans), size=1, prob=trans[estado,])
      
    cat(" -> ",proxEstado)

    estado <- proxEstado
    
  }
  cat("\n")
}

simulaMC() simula transições aleatórias até atingir 100 passos; simulaMC(10) simula até atingir 10 passos.

Exercício 92 Se é uma cadeia de Markov com matriz de transições

e é dada por e , então é uma cadeia de Markov?

Exercício 93 Mostre que a sequência de v.a. do exemplo 114 é de variáveis independentes 2-a-2, conclua que e que vale a identidade de Chapman–Kolmogorov (51) mesmo não sendo uma cadeia de Markov.

Classificação de estados

Os estados de uma cadeia de Markov são classificados em dois tipos fundamentais. Um estado é recorrente (ou, persistente) se, uma vez tendo estado nele, é certo que a cadeia eventualmente volta a ele, caso contrário, i.e. a probabilidade de retorno é menor que , então o estado é dito transiente (ou, transitório). Quando o estado é recorrente, a cadeia visita-o infinitas vezes pois a cada vez que chega no estado é como um reinicio, ela voltará a ele com probabilidade , e no caso transiente o estado é visitado um número finito de vezes. Notemos que isso leva a conclusão de que se é finito então pelo menos um estado é recorrente.

Seja a probabilidade do evento “primeira passagem por a partir do em passos”

assim é a probabilidade do primeiro retorno a em passos e definimos

que é a probabilidade de eventualmente retornar ao estado de origem . Com essa definição, um estado é recorrente se , caso contrário e chamamos de transiente.

Seja a v.a. indicadora do evento . Então a soma para todo das variáveis é o número de vezes que a cadeia visita o estado , que afirmamos acima ser finito se e só se é transiente. De fato, pelo exercício 49,

logo

Essa classificação de estados pode ser caracterizada pelas probabilidades de transições da maneira que deduziremos a seguir.

Lema 18 O estado é

• recorrente se e só se .

• transiente se e só se .

Demonstração: Pela linearidade da esperança,

e o lema segue das considerações acima.

No caso , temos uma função de massa de probabilidade para o tempo de recorrência (ou retorno) para , cuja média é chamada de tempo médio de recorrência (ou tempo médio de retorno) para

No caso de transiente convencionamos .

Dado que o retorno ao estado inicial é certo, é natural perguntar se o tempo médio de retorno é finito. No caso o estado é dito recorrente nulo, no caso de média finita, , o estado é dito recorrente positivo.

Exemplo 117 No exemplo 109, , , e para todo inteiro . A probabilidade de não retornar ao estado nos primeiros passos é

portanto (exerc. 25) a probabilidade de nunca voltar ao estado é ~ e a probabilidade de voltar ao no -ésimo passo é

e, a partir disso, o tempo médio de recorrência do estado é

Em resumo, é recorrente nulo.

Exercício 94 Prove que numa cadeia de Markov sobre um conjunto finito de estados, pelo menos um estado é recorrente e todo estado recorrente é positivo

Exercício 95 Prove que

Conclua que se é recorrente, então para todo tal que .

Conclua também que se é transiente, então para todo e que, portanto, , quando , para todo .

Exercício 96 Defina a variável aleatória

com a convenção de que se não é visitado então . Verifique que é transiente se e só se e, nesse caso, . Verifique também que

Exercício 97 Defina a variável aleatória

e defina . Prove que

e que

para definido no exercício acima.

Exercício 98 Seja um subconjunto de estados e defina

Mostre que se e

se . Agora defina

e mostre que se e que

se .

Os estados e da cadeia do exemplo 107, quando são atingidos a cadeia não muda mais de estado; nesses casos chamamos tais estados de absorvente, que é um estado recorrente positivo.

Exercício 99 Seja um estado absorvente numa cadeia de Markov tal que para todo estado da cadeia , para algum . Mostre que todos os estados, a não ser , são transientes.

Exemplo 118 Na cadeia representada pelo esquema abaixo o estado é absorvente, os estados e são transiente e os estados e são recorrentes

Periodicidade

Numa cadeia de Markov que pode ser representada como

se então só pode ocorrer na cadeia em instante da forma , , . Para o estado , as probabilidades de retorno positivas só ocorrem para , . Para o estado ocorre o mesmo fenômeno que no estado e o caso do estado é semelhante ao caso do estado .

O período de um estado numa cadeia de Markov é

Caso dizemos que é periódico, nesse caso a menos que seja múltiplo de , e caso dizemos que é aperiódico . No exemplo acima todos os estados são periódicos de período .

Observação 6 Notemos que para todo estado da cadeia devem existir instantes e tais que

e como devemos ter que divide . Fixando concluímos que todo para o qual é da forma para inteiro. Assim, podemos particionar em (nesse caso e ) para os valores de acima de modo que se então a menos que . Agora consideramos os estados na ordem ciclicamente e um passo da cadeia sai de um estado para um estado na classe a direita, e a cada passos a cadeia está de volta à mesma classe.

— Classificação das cadeias —

A condição para algum significa que a partir do estado a cadeia eventualmente atinge o estado em passos; nesse caso dizemos que é acessível a partir de e escrevemos . Quando não é acessível a partir de a probabilidade da cadeia chegar em saindo de é

Escrevemos se e e dizemos que os estados e se comunicam. Deixamos para o leitor a verificação de que define uma relação de equivalência sobre , i.e.,

1. ,
2. se , então ,
3. se e então ,

portanto, ela particiona em classes de equivalência. A importância dessa partição é pelo fato enunciado no exercício a seguir.

Exercício 100 Prove que recorrência e transiência são propriedades de classe de equivalência de , isto é, dois estados que se comunicam tem a mesma classificação. Ademais, estados que se comunicam têm o mesmo período.

Um conjunto é é irredutível se para todos , portanto, cada classe é um subconjunto irredutível.

Quando um conjunto não é irredutível, dizemos redutível. Quando há uma única classe de equivalência dizemos que a cadeia é uma cadeia de Markov irredutível.

Um cadeia (ou um conjunto de estados) irredutível é

• aperiódica se todos os seus estados o forem;
• periódica se todos os seus estados o forem;
• transiente se todos os seus estados o forem;
• recorrente se todos os seus estados o forem.

Exemplo 119 Uma cadeia de Markov com estados e matriz de transições

não corresponde a uma cadeia irredutível pois para todo inteiro

portanto .

Exemplo 120 Uma cadeia com estados e matriz de transições

é redutível pois é da forma

para e todo inteiro .

No exemplo 115 é fácil ver a partir do diagrama que a cadeia é irredutível. A cadeia do exemplo 107, claramente, não é irredutível por causa dos estados absorventes e . Toda cadeia com pelo menos dois estados e com pelo menos um deles absorvente é uma cadeia redutível.

Um conjunto é fechado se sempre que e .

Exemplo 121 No caso da cadeia com matriz de transições

A cadeia é redutível e o conjunto dos estados têm três classes de equivalência de comunicação . Os conjuntos e são irredutíveis e fechados. Os estados , e são transientes pois uma vez que a cadeia sai de um deles em direção aos conjuntos fechados, ela não volta mais a esses estados. Todos os estados têm período portanto a cadeia é aperiódica. Ainda

portanto .

Exemplo 122 (passeio aleatório) Vejamos o caso do passeio aleatório do exemplo 110, onde

Claramente, a cadeia é irredutível logo todos os estados são ou recorrentes ou transientes. Fixemo-nos no estado e vamos determinar .

Como é impossível estar num estado par com um número ímpar de movimentos

Após passos a cadeia estará de volta em se e só se metade dos passo foi num sentido (e.g., do estado atual para o maior, o que ocorre com probabilidade ) e metade no sentido oposto, portanto

onde significa que e . Agora, se então converge se, e só se, converge, portanto precisamos estudar a convergência de

No numerador e vale a igualdade se e somente se . Portanto a série é infinita se e só se e como a cadeia é irredutível e o recorrente, a cadeia é recorrente. Se então a cadeia é transiente.

Exemplo 123

Exercício 101 Se é uma matriz de transição tal que tem todas as entradas não-negativas para algum . É verdade que tem todas as entradas não-negativas para todo inteiro ?

Exercício 102 Considere a cadeia de Markov com estados e transições para todo , e , e para todo . Classifique os estados e determine os tempos médios de recorrência.

Essa classificação, num certo sentido, diz-nos que basta estudarmos as cadeias irredutíveis. Se está em alguma classe de equivalência de comunicação que é recorrente, então a evolução da cadeia se restringe a essa classe pois, assumindo que e de modo que , por conseguinte , temos de

contrariando o fato de ser recorrente. Se, por outro lado, no conjunto dos estados transientes implica em ou a cadeia ficar em (consulte seção XV.8 do Feller para a probabilidade desse evento) ou se mover para algum e não sair mais dessa classe.

Exemplo 124 Considere uma cadeia de Markov com matriz de transição

cujas classes de comunicação são que é recorrente, que é absorvente e que é transiente. Se o inicio é no estado , então a probabilidade com que a cadeia entra na classe recorrente é, condicionando em $X_1$, dada por

logo ; e com probabilidade a cadeia é absorvida em .

No caso da matriz de transição

as classes de comunicação são , e , respectivamente, recorrente aperiódica, transiente e recorrente periódica. Se é a probabilidade de entrar na primeira classe descrita acima a partir do estado , , então

cuja solução é e .

Uma classe de comunicação é dita fechada se sempre que e . Acima verificamos que toda classe recorrente é fechada.

Exercício 103 Mostre que toda classe fechada finita é recorrente.

— Distribuição invariante e Convergência ao equilíbrio —

Recordemos a matriz de transição e transição em dois passos do exemplo 116

Se formos um pouco mais adiante obtemos

Ainda, se fizermos , a distribuição inicial, então é a distribuição de . Por exemplo, para , a distribuição uniforme em , então temos de modo que . Analogamente, é a distribuição de e, em geral, para

é a distribuição de . Notemos que

portanto, para o vetor não muda e é igual a

Além disso na coluna vale

para pois para todo . Na última igualdade usamos que , portanto a conclusão é que não depende da distribuição inicial , isto é, independentemente do estado inicial, se for suficientemente grande então a probabilidade da cadeia de Markov estar em qualquer um dos estados é dada pelo vetor

Para e acima valem

Um vetor de probabilidades que satisfaz é chamado de distribuição invariante ou distribuição estacionária da cadeia de Markov com matriz de transições . O limite é o que chamamos de convergência ao equilíbrio.

Exemplo 125 Uma cadeia redutível com matriz de transição

tem distribuição estacionária para qualquer e, por exemplo, para temos que . O mesmo acontece com a matriz de transição

e é estacionário mas não há convergência. A cadeia é periódica. Considere uma cadeia de Markov com quatro estado e matriz de transições

nesse caso, e são vetores estacionários.

Quando é finito não é difícil ver que a convergência e a invariância estão intimamente relacionadas pois se então temos uma distribuição invariante pois

e

Quando não é finito isso não vale necessariamente, por exemplo, no caso assimétrico () do passeio aleatório em , exemplo 123, temos pois a cadeia é transiente, entretanto, não é uma distribuição.

Teorema 20 Uma cadeia de Markov irredutível tem uma distribuição estacionária se, e somente se, todos os estados são recorrentes positivos. O vetor estacionário é único e satisfaz

Ainda, se a cadeia for periódica então

A demonstração para o caso finito é dada no final do post.

Usando R:

 invariante = function() {
# Para determinar pi que satisfaz pi %*% trans = pi resolvemos o
# sistema (t(trans) - I) %* pi = 0 onde t() e' a matriz transposta e
# pi agora e' um vetor coluna. No lado direito trocamos a ultima linha
# por uma linha de 1's, e no lado esquerdo trocamos o vetor nulo por
# (0,0,...0,1), isso representa a restricao da soma das entradas de pi
# ser 1. Entao, resolvemos para pi.

##########################################
  trans <- matrix(c( 
    1/2 , 1/2 , 0 , 0 , 0 , 0 ,
    1/4 , 3/4 , 0 , 0 , 0 , 0 ,
    1/4 , 1/4 , 1/4 , 1/4 , 0 , 0 ,
    1/4 , 0 , 1/4 , 1/4 , 0 , 1/4, 
    0 , 0 , 0 , 0 , 1/2 , 1/2 ,
    0 , 0 , 0 , 0 , 1/2 , 1/2
    ), ncol=6, byrow=TRUE)



  n <- nrow(trans)
  a <- t(trans)
  for(i in 1:n)    {    a[i, i] <- a[i, i] - 1  }
  a[n, ] <- 1
  b <- rep(0, n)
  b[n] <- 1
  solve(a, b)
  
}

No caso da cadeia ser periódica de período então

e ser for recorrente

com (único) vetor de estacionário.

Observação 8 Se uma sequência converge , então a sequência das médias parciais também converge

portanto de (59) temos

e se é a v.a.~indicadora do evento então

em que é o número de visistas a no intervalo de tempo~ (veja o lema 18), ou seja,

Em palavras, é a fração média de visitas ao estado por unidade de tempo.

Teorema 21 (Teorema ergódico) Para qualquer cadeia de Markov irredutível

Exercício 104 Uma matriz quadrada com entradas não-negativas é duplamente estocástica se é estocástica e a soma das entradas de cada coluna é . Mostre que se é quadrada de ordem e duplamente estocástica então o vetor uniforme é invariante para .

Observação 9 No caso finito a existência de um vetor estacionário é garantido para qualquer matriz estocástica. Esse fato decorre do Teorema do Ponto Fixo de Brower: Para toda função contínua , onde é compacto e convexo, existe tal que . Agora, consideremos para todo a norma

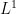
e o conjunto (compacto e convexo)

Seja uma matriz estocástica e considere a função linear de em dada por . Por ser linear a função é contínua, portanto, pelo Teorema da Ponto Fixo de Brower deduzimos a existência de um vetor estacionário.

— Cadeias redutíveis —

Os resultados da seção anterior aplicam-se a qualquer classe de comunicação recorrente. Se é classe de comunicação recorrente e aperiódica de um processo, então a submatriz formada pelos é estocástica logo quando .

Exemplo 126 Por exemplo,

tem as classes recorrentes com a submatriz estocástica irredutível

e com a submatriz estocástica irredutível

A matriz admite o vetor estacionário e a matriz , o vetor estacionário e, além disso

Ainda, se , com classe de comunicação recorrente e periódica, então

quando .

Por outro lado, se é um estado transiente então quando para qualquer estado inicial .

Exemplo 127 De volta ao exemplo 124, a classe recorrente com respeito a matriz tem distribuição estacionária . Ademais essa classe é atingida a partir do estado com probabilidade , portanto e logo

No que diz respeito a matriz , temos recorrente aperiódico com , transiente com probabilidade de sair de (respec., ) e ir ser absorvido por sendo (respec., ), e recorrente periódico

em que os espaços vazios indicam que o limite não existe. Entretanto,

— Exemplo: 2-SAT —

O 2-SAT (2-Satisfiability Problem) é o seguinte problema; dado uma fórmula booleana 2-CNF (cada cláusula é uma conjunção de 2 literais ), digamos

sobre um conjunto de variáveis , determinar se existe uma valoração que satisfaça .

É sabido [Aspvall, Plass, Tarjan, A linear-time algorithm for testing the truth of certain quantified Boolean formulas, Inform. Process. Lett., 1979, no.~3, pg.~121–123] que 2-SAT pode ser resolvido em tempo polinomial. A seguir, daremos um algoritmo aleatorizado bem simples, de tempo polinomial e que responde corretamente com alta probabilidade.

Exercício 105 Por que acima não define uma cadeia de Markov?

Exercício 106 Prove a afirmação feita no exemplo acima.

— Exemplo: Modelo de fecundidade —

As mudanças nos padrões sociais afetam a taxa de crescimento populacional. Modelos para analisar os efeitos das mudanças na fecundidade média de uma população levam em conta a idade, a situação conjugal, o número de filhos e várias outras informações a respeito do público feminino da população. Essas características compõem cada estado de um processo cujo interesse é determinar o tempo médio do processo nas categorias de maior fertilidade. As probabilidades de transição são inferidas de dados demográficos.

Num modelo simplificado consideramos os estados pré-puberil, solteira, casada, Divorciada, Viúva, morte ou emigração.

Denotemos por o tempo médio da cadeia no estado dado que . Então

cuja (única) solução é , , , .

Notemos que, como esperado, a distribuição estacionária é .

— Exemplo: Controle de estoque —

Uma mercadoria é armazenada e ao final dos preíodos o estoque é reabastecido. A demanda pela mercadoria no período é uma variável aleatória com independentes e identicamentes distribuídas..

A política de reabastecimento envolve escolher dois parâmetros inteiros e positivos e de modo que se ao final de um período o estoque é no máximo então ele é abastecido até atingir , caso contrário não é abastecido.

A variável aleatória é a quantidade de mercadoria ao fim do período antes do reabastecimento e caso seja negativa a demanda é atendida após o reabastecimento.

Os níveis de estoque em dois períodos consecutivos são realcionados por

e as probailidades das transições

Nesse caso, gostaríamos de saber qual é, a longo prazo, a fração de períodos que a demanda não é atendida

e qual é, a longo prazo, o nível médio de estoque

e sob certas condições converge.

Para um exemplo numérico tomemos

e e . Assim, .

Quando então não é necessário reabastecimento do estoque, logo caso , o que ocorre com probabilidade , logo . Agora, se então há reabastecimento para e caso , logo . A matriz fica da seguinte forma, lembrando que os estados são

que, claramente, é irredutível, recorrente e aperiódica, cujo vetor estacionário é

— Reversibilidade —

Numa cadeia de Markov, dado o estado presente, o futuro e o passado são independentes. Seja uma cadeia de Markov irredutível com respeito a matriz estocástica e a distribuição inicial , e uma distribuição invariante. Tomemos a matriz dada por

Essa matriz é estocástica pois, pela invariância de

Ainda,

ou seja, é invariante com relação a .

Se tomarmos para então

logo é uma cadeia de Markov com relação a e . Ademais,

portanto, a cadeia é irredutível, chamada tempo-reverso da cadeia .

Exercício 106 Mostre que se é uma matriz estocástica e um vetor não-negativo tal que para todos

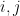
então .

Exercício 107 Prove que irredutível, com matriz de transições e distribuição inicial é reversível se e só se vale (64).

Exemplo 128 Consideremos um grafo conexo com peso positivo na aresta em cada aresta . Uma partícula move-se sobre o grafo com a seguinte estratégia: se a partícula encontra-se no vértice no instante então no instante a partícula estará no estado com probabilidade

de modo que caso não seja uma aresta. A equação (64) é equivalente a

No caso mais simples, e se e só se é aresta,

em que é o número de arestas incidentes em . Veremos que esse sempre é o caso, portanto passeios aleatórios em grafos são reversíveis.

— Demonstração do Teorema 13 no caso finito —

Vamos começar considerando o caso em que é uma matriz estocástica positiva. Digamos que é e definimos . Vamos provar que com uma matriz estocástica com as colunas constantes.

Exercício 108 Seja uma matriz estocástica com todas entradas positivas. Tomemos e um vetor coluna qualquer com e . Sejam e . Prove que , e
(Sugestão: tome o vetor obtido a partir de trocando todas as coordenadas por menos a coordenada ; tome o vetor obtido a partir de trocando todas as coordenadas por menos a coordenada . Use o fato de .)

Denotemos por o vetor coluna com todas as entradas nulas a menos da posição que é 1. A seguir, vamos usar o exercício anterior para definir um vetor estocástico que são as linhas de , o qual mostraremos depois ser estacionário.

Fixamos , uma coluna de , e definimos

o mínimo e o máximo, respectivamente, da -ésima coluna de , tomamos e . Para temos

Analogamente, temos

Do exercício 108 temos a sequência de máximos e mínimos

de modo que

pois . Da equação anterior e definimos

Com isso provamos que todas as entradas da -ésima coluna de convergem para um valor constante . Feito isso para cada coluna , o vetor que procuramos é

e com isso

e tomamos , a matriz com cada linha igual a que queríamos provar. Como temos , portanto . Também, .

Exercício 109 Prove que temos no vetor dado acima.

Estenderemos esse resultado para matrizes não negativas usando o fato de que para a matriz de uma cadeia de Markov irredutível e aperiódica temos positiva para algum .

Proposição 22 Se uma cadeia Markov é ergódica então existe tal que para todo , se então .

Demonstração: Da cadeia ser irredutível temos que para cada existe tal que . Da cadeia ser aperiódica temos que para cada existe tal que para todo . Com essas constantes, se então

portanto, por (52), para todo

Tomamos

o que prova a proposição.

O vetor é estacionário

Agora, provaremos que se o estado inicial é algum elemento de com probabilidade dada por então quando , ou seja, qualquer distribuição inicial a longo prazo se aproxima da distribuição estacionária.

Consideremos os vetores de probabilidades

e

e a partir de obtemos a distribuição por

Agora, seja a constante dada pela proposição 22. Assim, é uma matriz com todas as entradas positivas e para e para

portanto, a subseqüência converge, . Ademais, as diferenças nunca aumentam com , ou seja, a seqüência é não-crescente, portanto converge para , portanto,

Seja um vetor qualquer com . Para mostrar a unicidade de é suficiente mostrar que é um múltiplo escalar de .

Se então , portanto

logo e podemos concluir então que .

Agora, vamos provar que para qualquer vetor de probabilidades . Como acima,

donde é a -ésima coordenada de . Como é um vetor de probabilidades a soma das coordenadas é , logo

ou seja, como queríamos provar.

Resta provar que . Como é finito .

Primeiro, definimos para , e se consideramos o primeiro passo da cadeia temos que vale

De modo análogo Esse conjunto de equações pode ser escrito de forma matricial como

em que é a matriz com todas as entradas iguais a e é a matriz diagonal . Reescrevendo temos

em que é a matriz identidade. Se multiplicarmos por a direita nos dois lados da igualdade temos, no lado direito, que pois é estacionário, portanto , mas , logo para cada , isto é,

— Exercícios complementares —

Exercício 116 Seja uma matriz de transições de uma cadeia de Markov. Defina a matriz . Prove que a cadeis com matriz de transições é aperiódica.

Exercício 117 Considere a generalização natural do algoritmo para o 2-SAT, seção 0, para 3-SAT. Prove que tal algoritmo é exponencial, em que é o número de variáveis.

Exercício 118 Por dia, uma dentre pessoas é requisitada, a pessoa requisitada com probabilidade . As pessoas são organizadas numa lista ordenada e a cada requisição a pessoa escolhida é colocada no topo da lista, o resto da lista fica inalterada.

1. Numa modelagem com cadeia de Markov, quais são os estados?
2. Qual é a distribuição invariante? (Dica: Não precisa fazer conta.)

Exercício 119 Uma pessoa tem guarda-chuvas que usa no trajeto de casa ao trabalho e vice-versa. Se ela está em casa no começo de dia e está chovendo então escolhe um guarda-chuva para ir ao escritório, caso haja disponível. Se ela está no escritório no fim do dia e está chovendo então escolhe um guarda-chuva para ir para casa, caso haja disponível. Quando não está chovendo ela não escolhe usa guarda-chuva. Assumindo que no início do dia e no fim do dia chove de modo independente e com probabilidade , qual é a fração das viagens que ela faz sob chuva e sem guarda-chuva?

Exercício 120 Um grupo de processadores é arranjado em lista ordenada e quando uma tarefa chega é atribuída ao primeiro da lista; se ele está ocupado tenta-se o segundo da lista, e assim por diante. Uma vez que a tarefa é processada ou que não é encontrado um processador disponível pra ela, ela deixa o sistema. Nesse momento, podemos reordenar os processadores antes que a próxima tarefa chegue e a estratégia é: se um processador atendeu a tarefa ele avança uma posição na lista, trocando-o com o processador imediatamente a frente; se todos falharam ou o primeiro atendeu a ordem permanece a mesma. Assumamos que no processador atende a tarefa com probabilidade .

1. Defina uma cadeia de Markov para analisar o problema.
2. Mostre que a cadeia é reversível.
3. Descubra as probabilidades limite.

Exercício 121 Num tabuleiro de xadrez o cavalo começa num dos quatro cantos e se move com igual probabilidade para qualquer uma das posições legais, de acordo com as regras do seu movimento. Qual é o número esperado de movimentos até voltar para a posição de saída?

Exercício 122 Como podemos gerar valores para vinte variáveis aleatórias independentes e com distribuição uniforme em condicionadas a soma delas serem menor que dois?

Exercício 123 Uma coloração de um grafo é uma atribuição de cores aos vértices do grafo. Um grafo é -colorível se há um coloração com cores sem que vértices adjacentes recebam a mesma cor. Seja um grafo -colorível.

Mostre que tem uma coloração com 2 cores sem que haja triângulo com os três vértices da mesma cor.

Considere o seguinte algoritmo para achar a coloração afirmada no parágrafo acima: o algoritmo começa com uma coloração de duas cores arbitrária. Enquanto houver triângulo monocromático, escolha um deles e sorteie um de seus vértices, mude a cor do vértice sorteado. Determine um limitante superior para o número esperado de recolorações até oal goritmo terminar.

Exercício 124 Seja a soma dos resultados de lançamentos independentes de um dado. Mostre que para

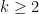
Exercício 125 Numa cidade com habitantes, uma pessoa conta um boato para uma segunda pessoa, que por sua vez conta o boato para uma terceira pessoa e assim por diante. Em cada passo o ouvinte do boato é escolhido aleatoriamente de maneira uniforme dentre as outras pessoas na cidade. Como esse processo pode ser modelado como uma cadeia de Markov? Qual a probabilidade do boato ser contado vezes sem repetir nenhuma pessoa? Escreva um código em para determinar o número de rodadas até que todos tenham ouvido o boato com probabilidade , para .

Exercício 126 Um gato e um rato passeiam aleatoriamente num grafo conexo e não-bipartido de modo independente. Eles começam ao mesmo tempo em vértices diferentes e ambos dão um passo a cada instante, também de modo independente. O gato come o rato se em algum instante eles estão no mesmo vértice. Mostre que o número esperado de passos até els se encontrarem é , em que é o número de vértice e o número de arestas de . (Dica: considere a cadeia de Markov com estados sendo as posições de cada animal no grafo, num instante.)

Exercício 127 O grafo Lollipop é um grafo completo com vértices e um caminho com vértices e um único vértice em comum. Chamamos de o úico vértice de grau um, o vértice final do caminho.

Mostre que se um passeio aleatório começa em então o número esperado de passos até visitar todos os vértices é .

Mostre que se um passeio aleatório começa em então o número esperado de passos até visitar todos os vértices é .