bc1405 – Teorema Fundamental da Aritmética, Distribuição de primos e Pequeno Teorema de Fermat

— Números primos e Teorema Fundamental da Aritmética —

Um natural ${p > 1}$ é primo se os únicos divisores de ${p}$ são ${1}$ e ${p}$ ; se ${p>1}$ não é primo então é dito composto; logo, por definição, se ${p}$ é composto então admite um divisor ${d}$ tal que ${1<d<n}$ .

Exercicio 18 Se ${a\neq 0,1}$ e

$\displaystyle d(a):= \{ n \colon n>1 \text{ e } n|a\} \ \ \ \ \ (26)$

então o menor elemento de ${d(a)}$ é um número primo.

Demonstração: ${d(a) \neq\emptyset}$ pois ${a\in d(a)}$ . Se ${m:=\min d(a)}$ é composto então ${m=dq}$ para algum ${d}$ , ${1<d<m}$ . Como ${d|m}$ e ${m|a}$ temos, por transitividade, ${d|a}$ .

Como ${m}$ é menor elemento de ${d(a)}$ e ${d<m}$ , temos ${m\not\in d(a)}$ , ou seja, ${d\leq 1}$ , uma contradição. $\Box$

Proposição 10 (Proposição 30, Euclides, 300 aC) Sejam ${a,b\neq 0}$ naturais. Se ${p}$ é primo e ${p|ab}$ então ${p|a}$ ou ${p|b}$ .

Demonstração: Sejam ${a,b,p}$ naturais como enunciado. Se ${p\not|a}$ então ${\mathrm{mdc}(p,a)=1}$ e pelo exercício 17, item 3, ${p|b}$ . Analogamente, ${p\not|b\Rightarrow p|a}$ . $\Box$

Corolário Se ${p}$ é primo e ${p|a_1a_2\cdots a_n}$ , então ${p|a_i}$ para algum ${i}$ .

Demonstração: Segue por indução (verifique). $\Box$

Teorema 11 (Teorema Fundamental da Aritmética) Todo natural maior que ${1}$ ou é primo ou pode ser escrito de maneira única, a menos da ordem dos fatores, como um produto de primos.

Demonstração: Provemos usando indução em ${n}$ que o predicado ${P(n):=}$ ” ${n}$ ou é primo ou é produto de primos” é verdadeiro para todo ${n>1}$ .

${P(2)}$ é verdadeiro.

Suponha ${k>1}$ é um natural e ${P(n)}$ é verdadeiro para todo ${n\in \{2,3,4,\dots,k\}}$ . Provaremos que ${P(k+1)}$ é verdadeiro. Pelo exercício 18

$\displaystyle m:= \min d(k+1)$

é primo. Se ${m=k+1}$ , então ${k+1}$ é primo, senão ${1< m< k+1}$ é um primo que divide ${k+1}$ , i.e, tal que ${k+1 = m\cdot q}$ . Como ${q < k+1}$ , ${P(q)}$ é verdadeiro, ou seja, ${q}$ é primo ou um produto de primos, logo ${ m\cdot q}$ é produto de primos.

Pela 2ª forma do PIF, ${P(n)}$ é verdadeiro para todo ${n>1}$ .

Agora, provaremos que a escrita de ${n}$ como produto de primos é única a menos da ordem dos fatores. Se esse não é o caso, seja ${n}$ o menor natural que pode ser escrito como diferentes produtos de primos

$\displaystyle n= p_1p_2\cdots p_a=q_1q_2\cdots q_b$

com ${p_1 \leq p_2\leq \cdots\leq p_a}$ e ${q_1\leq q_2\leq \cdots \leq q_b}$ primos. Então

$\displaystyle p_1|q_1q_2\cdots q_b$

e pelo Corolário acima ${p_1|q_j}$ para algum ${j}$ , logo ${p_1=q_j \geq q_1}$ . Analogamente,

$\displaystyle q_1|p_1p_2\cdots p_b$

logo para algum ${i}$ , ${q_1=p_i \geq p_1}$ . Portanto, ${p_1=q_1}$ . Pela minimalidade de ${n}$ ,

$\displaystyle p_2\cdots p_a=q_2\cdots q_b$

é o mesmo produto de primos, uma contradição. $\Box$

Assim, para todo ${n>1}$ existem ${p_1<p_2<\cdots < p_k}$ primos e ${\alpha_1,\alpha_2,\dots,\alpha_k \in {\mathbb N}\setminus\{0\}}$ tais que

$\displaystyle n= p_1^{\alpha_1}p_2^{\alpha_2}\cdots p_k^{\alpha_k} \ \ \ \ \ (27)$

que chamamos de fatoração canônica de ${n}$ em primos. Por exemplo

$\displaystyle 84= 2^2\cdot 3\cdot 7 ~\text{ e }~120 = 2^3\cdot 3\cdot 5 ~\text{ e }~350= 2\cdot 5^2 \cdot 7$

Exercicio 19 Quantos divisores tem ${n}$ , para qualquer ${n>1}$ ?

Solução:

$\displaystyle \sigma(n):= (\alpha_1+1)(\alpha_2+1)\cdots(\alpha_k+1) \ \ \ \ \ (28)$

$\Box$

Exercicio 20 ${\sigma(n)}$ é ímpar se, e só se, ${n}$ é um quadrado perfeito.

— Distribuição dos primos —

Crivo de Eratóstenes

Notação ${\lfloor \sqrt{n} \rfloor := \max\{x\in{\mathbb N}\colon x^2\leq n\}}$ .

Os números primos até ${n}$ podem ser obtidos por

Liste todos os números de ${2}$ até ${n}$ ;
Para cada ${i\in \{2,3,\dots,\lfloor \sqrt{n} \rfloor\}}$ : se ${i}$ está na lista então apague os múltiplos de ${i}$ maiores que ${i}$ .

conhecido como Crivo de Eratóstenes. Por exemplo, para conhecer os primos menores que 60 excluímos das lista ${2,\dots,60}$ os múltiplos de ${2,~3,~5, ~7}$ .

Os naturais que sobram depois desse processo não são divisíveis pelos naturais ${x\in\{2,3,\dots,\lfloor \sqrt{n} \rfloor\}}$ para os quais vale que ${x^2 \leq n}$ por definição de ${\lfloor \sqrt{n} \rfloor}$ .

Lema 12 (Eratóstenes, 230 ac) Se ${n>1}$ não é divisível por nenhum dos primos ${p}$ tais que ${p^2 \leq n}$ então ${n}$ é primo.

Demonstração: Se ${n}$ é composto então tomamos ${q}$ o menor primo que divide ${n}$ . Então ${n=qm}$ com ${q\leq m}$ , logo ${q^2 \leq mq=n}$ e ${q|n}$ , uma contradição. $\Box$

Distribuição dos primos

A distribuição dos números primos dentro de ${{\mathbb N}}$ tem muitos problemas desafiadores, como a conjectura dos primos gêmeos, da infinitude de números de Fibonacci (respec., de Mersenne; respec., perfeitos) que são primos. Além desses, existe um primo entre ${n^2}$ e ${(n+1)^2}$ ? Existem infinitos primos da forma ${n^2-n+41}$ ? São perguntas difíceis de responder a respeito da distribuição dos primos. Um resultado importante nesse contexto que não provaremos aqui é o Teorema dos Números Primos: se ${\pi(x)}$ é a quantidade de primos que são menores ou iguais a ${x}$ , então

$\displaystyle \lim_{x\rightarrow\infty} \frac{\pi(x)}{\frac{x}{\log(x)}} = 1 \ \ \ \ \ (29)$

Denotamos por ${p_n}$ o ${n}$ -ésimo número primo. A conjectura dos primos gêmeos pergunta se ${|\{n\colon p_{n+1}-p_n =2\}|\stackrel{\mathrm{?}}{=}|{\mathbb N}|}$ .

Sabemos que há primos consecutivos arbitrariamente distantes:

Exercicio 21 Para todo ${n}$ , existem ${n}$ naturais consecutivos e compostos.

Demonstração: ${(n+1)!+2,(n+1)!+3,\dots,(n+1)!+n+1}$ é divisível, respectivamente, por ${2,3,\dots,n+1}$ $\Box$

Em geral sabemos pouco sobre o comportamento de ${p_{n+1}-p_n}$ . Se verdadeira, a conjectura dos primos gêmeos implica em ${\liminf (p_{n+1}-p_n)=2}$ . Até recentemente não se sabia se ${\liminf (p_{n+1}-p_n)}$ é finito, quando em 2013 Zhang mostrou que ${\liminf (p_{n+1}-p_n) < 70000000}$ ; o que tem sido melhorado e no momento vale ${\liminf (p_{n+1}-p_n) < 246}$ .

Teorema 13 Há infinitos números primos.

Demonstração: Se ${p_1,p_2,\dots,p_r}$ são todos os números primos então

$\displaystyle n= p_1p_2\cdots p_r +1$

pode ser escrito como o produtos desses primos, mas se ${p_i|n}$ então ${p_i|1}$ , um absurdo. $\Box$

Demonstração: Vamos mostrar que para todo natural ${n}$ existe um primo maior que ${n}$ . Para tal, tome ${p}$ um fator primo do número ${n!+1}$ . Se ${p\leq n}$ então ${p|n!}$ por definição de fatorial. Se ${p}$ divide ${n!}$ e ${n!+1}$ então ${p}$ divide a diferença desses números, i.e., ${p|1}$ , portanto ${p=1}$ , um absurdo que estabelece ${p>n}$ . $\Box$

Lema 14 Há infinitos primos da forma ${4k+3}$ .

Demonstração: A prova é um exercício com o seguinte roteiro:

Todo primo ímpar é da forma ${4k+1}$ ou ${4k+3}$ .
O produto de dois números da forma ${4k+1}$ também é dessa forma.
Para quaisquer ${p_1,dots,p_r}$ , ${N=4(p_1\cdots p_r)-1}$ é da forma ${4k+3}$ e existe um primo ${p}$ da forma ${4k+3}$ tal que ${p|N}$ .
Suponha que na descrição de ${N}$ os naturais ${p_1,\dots,p_r}$ acima sejam todos os primos da forma ${4k+3}$ . Determine a existência de um primo da forma ${4k+3}$ que não seja nenhum dos listados acima.

$\Box$

O teorema 13 afirma que na sequência

$\displaystyle 1,2,3,4,5,6,\dots,n,n+1,\dots$

há infinitas ocorrências de números primos. O Lema 14 afirma que o mesmo ocorre na sequência

$\displaystyle 3, 7 , 11 , 15 , 19 , 23 , 27 , 31 , 35 , 39 , 43 , 47 , \dots, 4n+3, 4(n+1)+3,\dots$

e um teorema famoso da Teoria Analítica dos Números, o Teorema de Dirichlet, afirma que o mesmo ocorre com a sequência (ou melhor, na progressão aritmética que começa em ${a}$ e tem razão ${d}$ )

$\displaystyle a, a+d, a+2d, a+3d, \dots, a+nd, a+(n+1)d,\dots$

para quaisquer ${a,d}$ coprimos.

— Pequeno Teorema de Fermat (PTF) —

Para ${0\leq b\leq a}$ , é possivel provar que ${(b!(a-b)!)\, |\, b!}$ (exercício). Definimos

$\displaystyle \binom ab := \frac{a!}{b!(a-b)!} \ \ \ \ \ (30)$

e vale para todo ${n}$ (outro exercício)

$\displaystyle (a+b)^n = \sum_{i=0}^n \binom ni a^ib^{n-i}. \ \ \ \ \ (31)$

Exercicio 22 Se ${p}$ é primo então ${\binom pi}$ é divisível por ${p}$ para todo ${0<i<p}$ .

Teorema 15 (Pequeno Teorema de Fermat) Se ${p}$ é primo então ${p| (a^p-a)}$ para todo ${a\geq 1}$ .

Demonstração: Para ${a=1}$ a afirmação certamente vale. Suponha que vale para ${a}$ e vamos provar que vale para ${a+1}$ .

$\displaystyle (a+1)^p - (a+1) = \sum_{i=0}^p \binom pi a^i 1^{p-i} - (a+1) =(a^p -a) + \sum_{i=1}^{p-1} \binom pi a^i 1^{p-i}$

e como ${p|(a^p -a)}$ e ${p|\binom pi}$ ( ${0<i<p}$ ) temos ${p|[(a+1)^p - (a+1)]}$ . $\Box$

Notemos que ${p| (a^p-a) \Rightarrow p|a (a^{p-1}-1)}$ , portanto, se ${p\not| a}$ então ${p|(a^{p-1}-1)}$

Corolario 16 (também chamado de Pequeno Teorema de Fermat) Se ${p}$ é primo e ${p\not| a}$ , então ${p| (a^{p-1}-1)}$ . ${\Box}$

Exemplo.
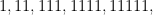
Se ${p\neq 2,5}$ é primo, ${p}$ divide algum número dentre ${1 , 11 , 111 , 1111 , 11111,}$ ${111111,1111111,\dots}$ . Se ${p=3}$ então ${p}$ divide todo número com quantidade divisível por ${3}$ de algarismos ${1}$ . Se ${p>5}$ então ${\mathrm{mdc}(10,p)=1}$ portanto ${p| 10^{p-1}-1 = 9\cdot 1111\cdots11}$ e como ${p\not| 9}$ temos ${p|1111\cdots11}$ .

Exemplo.
${10|(n^9-n)}$ . Como ${n^9}$ e ${n}$ têm a mesma paridade, ${2|(n^9-n)}$ . Vamos verificar que ${5|(n^9-n)}$ que, como ${\mathrm{mdc}(2,5)=1}$ , concluímos que ${10|n^9-n}$ .

$\displaystyle n^9-n = n(n^4-1)(n^4+1) = (n^5-n)(n^4+1)$

O PTF garante que ${5|(n^5-n)}$ , portanto ${10|(n^9-n)}$ ; em outras palavras ${n^9}$ e ${n}$ têm o mesmo algarismo da unidade em base ${10}$ .

De acordo com o teorema de Fermat, dados inteiros ${n}$ e ${a}$ , se ${n}$ é primo e não divide ${a}$ então ${a^{n-1}\,\mathrm{mod}\, n = 1}$ , portanto, qualquer outro resultado indica que ${n}$ é composto. Entretanto, o teorema não garante que se ${a^{n-1}\,\mathrm{mod}\, n = 1}$ então ${n}$ é primo.

Por exemplo ${2340 \; \mathrm{mod}\; 341 =1}$ mas ${341 = 11 \cdot 31}$ não é primo. Em algumas referências tais números são ditos pseudo-primos de Fermat. Um número inteiro ímpar e composto ${n}$ é um pseudo-primo para a base ${a}$ se ${a^{n-1}\;\mathrm{mod}\; n = 1}$ . Assim, ${341}$ é pseudo-primo para a base ${2}$ . De fato, é o menor pseudo-primo para a base ${2}$ . Podemos descobrir que ${341}$ é composto testando-o contra outras bases e nesse caso ${3340 \; \mathrm{mod}\; 341 =54}$ o que atesta que ${341}$ é composto. Entretanto, estender essa estratégia não produz um algoritmo eficiente para decidir primalidade. Não há números que sejam pseudo-primos para toda base ${a\in\{2,\dots,n- 2\}}$ pois se ${\mathrm{mdc}(a,n) > 1}$ então ${a^{n-1}\;\mathrm{mod}\; n \neq 1}$ . Isso garante que se incrementamos a base e fazemos o teste de Fermat então o mais longe que iremos é até o menor divisor primo de ${n}$ , mas isso pode não ser muito mais eficiente do que usar crivo de Eratóstenes.

— Exercícios —

Para quais valores de ${m}$ e ${n}$ o número ${9^m10^n}$ tem 27 divisores?
Qual é a forma geral de um número que tem só mais um divisor além do ${1}$ e dele mesmo?
Prove que se ${\mathrm{mdc}(n,m)=1}$ então ${\sigma(n\cdot m) =\sigma(n)\sigma(m)}$ .
Verifique as afirmações.
1. 287 é primo.
2. Todo primo da forma ${3k+1}$ é da forma ${6q+1}$ .
3. Entre ${n}$ e ${n!}$ existe um primo.(Dica: considere ${n!-1}$ )
Deduza da coprimalidade dos números de Fermat (exemplo 5) que há infinitos números primos.
Todo primo maior que ${6}$ é da forma ${6k+1}$ ou ${6k+5}$ .
Mostre que há infinitos primos da forma ${6k+5}$ .
O único primo da forma ${n^3+1}$ é ${7}$ .
Se a soma de dois naturais não-nulos é primo, esses números são coprimos?
Todo primo da forma ${3n+1}$ é da forma ${6m+1}$ .
Considere os inteiros positivos com as respectivas fatorações canônicas ${a= p_1^{\alpha_1}p_2^{\alpha_2}\cdots p_k^{\alpha_k}}$ e ${b= p_1^{\beta_1}p_2^{\beta_2}\cdots p_k^{\beta_k}}$ . Defina
$\displaystyle \gamma_i := \max\{\alpha_i,\beta_i\}$

$\displaystyle \delta_i := \min\{\alpha_i,\beta_i\}$

e prove que

$\displaystyle \mathrm{mdc}(a,b) = p_1^{\delta_1}p_2^{\delta_2}\cdots p_k^{\delta_k}$

$\displaystyle \mathrm{mmc}(a,b) = p_1^{\gamma_1}p_2^{\gamma_2}\cdots p_k^{\gamma_k}$
Vamos mostrar que há infinitos primos estabelecendo que .
1. Dizemos que ${r}$ é livre de quadrado se não tem um divisor diferente do ${1}$ que é um quadrado perfeito. Equivalentemente, ${r= p_1^{\alpha_1}p_2^{\alpha_2}\cdots p_k^{\alpha_k}}$ com ${\alpha_i=0,1}$ para cada ${i}$ . Prove que a quantidade de naturais menores ou iguais a ${n}$ livres de quadrado é no máximo ${2^{\pi(n)}}$ .
2. Prove que todo ${m\leq n}$ é da forma ${m= s^2 \cdot r}$ , com ${r}$ livre de quadrado e ${s^2\leq m}$ .
3. Use os itens anteriores para provar que ${n\leq 2^{\pi(n)}{\lfloor \sqrt n \rfloor}}$ .
4. Prove que ${\pi(n) \geq \frac 12\log_2(n)}$ .