bc0406 – Probabilidade Condicional e Independência

Consideremos uma escolha aleatória de uma família com dois filhos. O espaço amostral é

$\displaystyle \Omega = \big\{ (H,H),(H,F),(F,H),(F,F)\big\}$

e a probabilidade de cada evento elementar é ${\frac 14}$ . Qual é a probabilidade de ambos serem meninos sabendo-se que pelo menos um deles é menino? Dado que um menino, a resposta é um elemento de ${\{ (H,H), (H,M), (M,H)\big\}}$ , portanto a probabilidade de ambos serem meninos é ${1/3}$ . Retomemos o modelo clássico para motivar a definição de probabilidade condicional. Se ${A}$ e ${B\neq\emptyset}$ são eventos de ${\Omega}$ e se ocorreu um dos ${|B|}$ pontos amostrais de ${B}$ , então ${A}$ ocorre se um dos ${|A\cap B|}$ pontos amostrais de ${A\cap B}$ ocorre de modo que a probabilidade com que ${A}$ ocorre se é sabido que ${B}$ ocorre é

$\displaystyle \frac{|A\cap B|}{|B|} = \frac{\frac{|A\cap B|}{|\Omega|}}{\frac{|B|}{|\Omega|}}= \frac{\mathop{\mathbb P}(A\cap B)}{\mathop{\mathbb P}(B)}.$

Num modelo probabilístico ${(\Omega,\mathcal{A},\mathop{\mathbb P})}$ a probabilidade condicional do evento ${A}$ com respeito ao evento ${E}$ , em que ${\mathop{\mathbb P}(E)>0}$ , é definida por

$\mathop{\mathbb P}(A ~|~ E) =\frac{\mathop{\mathbb P}(A\cap E)}{\mathop{\mathbb P}(E)}$

e ${\mathop{\mathbb P}(A ~|~ E)}$ é lido como a probabilidade de ${A}$ dado ${E}$ .

Proposição 11 (Teorema da Multiplicação) Se ${A}$ e ${B}$ são eventos de um modelo probabilístico com ${\mathop{\mathbb P}(A)>0}$ então

$\mathop{\mathbb P}(A \cap B) = \mathop{\mathbb P}(B ~|~ A) \mathop{\mathbb P}(A) .$

Analogamente, ${\mathop{\mathbb P}(A \cap B) = \mathop{\mathbb P}(A ~|~ B) \mathop{\mathbb P}(B)}$ , quando ${\mathop{\mathbb P}(B)>0}$ .

Exemplo 18 Dois dados, um azul e outro verde, são lançados e cada uma das seis faces são equiprováveis nos dois dados. Qual é a probabilidade do dado verde ter resultado 6 dado que a soma dos resultados foi 8? O espaço amostral tem ${36}$ elementos equiprováveis, formado pelos pares ordenados dos resultados possíveis. Os eventos de interesse são

$\displaystyle E\equiv \textrm{ ``a soma \'e 8''} \qquad E=\{(2,6),(3,5),(4,4),(5,3),(6,2)\}$

$\displaystyle A\equiv \textrm{ ``no verde saiu 6''}\qquad A=\{(x,6)\colon1\leq x\leq6,\;x\in\mathbb{N}\}$

A probabilidade que procuramos é

$\displaystyle \mathop{\mathbb P}(A~|~E) = \frac{\mathop{\mathbb P}(A\cap E)}{\mathop{\mathbb P}(E)}= \frac{\mathop{\mathbb P}\left(\big\{(2,6)\big\}\right)}{\mathop{\mathbb P}(E)}= \frac{1/36}{5/36}=\frac 15.$

Exemplo 19 Numa cômoda há três gavetas e em cada gaveta um par de meias. Na primeira gaveta há um par de meias brancas, na segunda um par de meias pretas e na terceira gaveta um par com um pé de meia de cada cor, preta e branca. Uma das três gavetas é escolhida ao acaso e em seguida, sem olhar para o interior da gaveta escolhida, essa gaveta é aberta e um pé de meia é escolhido aleatoriamente dentre os dois pés daquela gaveta; a gaveta escolhida é fechada. O pé de meia retirado é branco. Qual a probabilidade de o outro pé que ficou sozinho na gaveta ser preto?

Se ${E}$ é o evento “retirou uma meia branca”, e ${A}$ o evento “ficou uma meia preta”, então ${\mathop{\mathbb P}(A\cap E) = 1/6}$ e ${\mathop{\mathbb P}(E)=1/2}$ , logo

$\displaystyle \mathop{\mathbb P}(A~|~E)=\frac{\mathop{\mathbb P}(A\cap E)}{\mathop{\mathbb P}(E)}= \frac 13.$

Nesse exemplo podemos construir um modelo probabilístico considerando o espaço amostral formado pelos pares ${(\mathrm{gaveta},\mathrm{cor~ da~ meia ~retirada})}$ , com as gavetas numeradas de um a três

$\displaystyle \begin{array}{rcl} \Omega = \big\{ & (1,\mathrm{branca}), (2,\mathrm{preta}),&\\ & (3,\mathrm{preta}),(3,\mathrm{branca})&\big\} \end{array}$

com os eventos elementares da primeira linha 2 vezes mais prováveis (por quê?; reveja o exemplo Monty Hall) que os da segunda, de modo que cada um dos dois primeiros eventos elementares listados no espaço amostral têm probabilidade ${1/3}$ e o outros dois probabilidade ${1/6}$ cada. Os eventos são

$\displaystyle E=\{(1,\mathrm{branca}), (3, \mathrm{branca})\} ~ e ~ A=\{(2,\mathrm{preta}),(3,\mathrm{branca})\},$

e, só conferindo, ${ \mathop{\mathbb P}(A~|~E) = {\mathop{\mathbb P}\big((3,\mathrm{branca})\big)} \big/ { \mathop{\mathbb P}\big( \big\{ (1,\mathrm{branca}),(3,\mathrm{branca})\big\}\big)}=1/3}$ .

Exemplo 20 No problema do exercício 31 os eventos que interessam são ${E\equiv}$ “a face exibida é laranja” e ${A\equiv}$ “a face não-exibida é laranja”. Como metade das faces são laranjas, ${\mathop{\mathbb P}(E)=1/2}$ . Só uma das cartas tem as duas faces laranjas logo ${\mathop{\mathbb P}(A\cap E)= 1/3}$ , assim a probabilidade que interessa é

$\displaystyle \mathop{\mathbb P}(A~|~E)=\frac{\mathop{\mathbb P}(A\cap E)}{\mathop{\mathbb P}(E)}= \frac{1/3}{1/2}=\frac 23.$

Descreva detalhadamente o espaço amostral e os eventos desse experimento.

Exercicio 33 (Lewis Carrol) Leia a seguinte “prova” de que uma urna não pode ter duas bolas da mesma cor:
Uma urna contém um par de bolas que podem ser da cor branca ${(B)}$ ou preta ${(P)}$ , de modo que ${\mathop{\mathbb P}( BP ) = \mathop{\mathbb P}( PB ) = \mathop{\mathbb P} ( PP ) = \mathop{\mathbb P}( BB ) = \frac 14}$ . Adicionamos uma bola preta de modo que ${\mathop{\mathbb P}( PBP ) = \mathop{\mathbb P}( PPB ) = \mathop{\mathbb P} ( PPP ) = \mathop{\mathbb P}( PBB ) = \frac 14}$ . Agora, sorteamos uma bola e a probabilidade que essa bola é preta é, usando probabilidade condicional

$\displaystyle 1\cdot \frac 14 + \frac 23 \cdot \frac 14 + \frac 23 \cdot \frac 14 + \frac 13 \cdot \frac 14 = \frac 23.$

Se a probabilidade de sortear uma bola preta é ${\frac 23}$ então o par original de bolas não pode ser ${PP}$ nem ${BB}$ , ou seja, não podem ter a mesma cor. Faça uma análise criteriosa dessa (falsa) dedução.

Exercicio 34 Seja ${\mathop{\mathbb P}}$ é uma medida de probabilidade para os eventos em ${\mathcal A}$ e ${E\in\mathcal A}$ um evento com probabilidade positiva. Defina a função ${{\mathbb Q}\colon \mathcal A \rightarrow {\mathbb R}}$ por

$\displaystyle {\mathbb Q}(A) \stackrel{\textrm{\tiny\textrm{def}}}{=} \mathop{\mathbb P}(A~|~E).$

Prove que ${{\mathbb Q}}$ é uma medida de de probabilidade para os eventos em ${\mathcal A}$ (i.e, mostre que ${\mathbb{Q}}$ satisfaz os axiomas de probabilidade a partir do fato de que ${\mathop{\mathbb P}}$ os satisfazem).

— Teorema da Probabilidade Total —

Observemos que se ${E}$ e ${A}$ são eventos, ${0<\mathop{\mathbb P}(E)<1}$ , então ${A}$ ocorre se e só se

${A}$ e ${E}$ ocorre

${A}$ e ${\overline E}$ ocorre

e ${\{A \cap E , A \cap \overline E\}}$ é uma partição de ${A}$ , logo de ${A = \big( A \cap E\big) \cup \big( A \cap \overline E\big)}$ deduzimos

$\displaystyle \begin{array}{rcl} \mathop{\mathbb P}(A) &=& \mathop{\mathbb P}\Big(\big( A \cap E\big) \cup \big( A \cap \overline E\big)\Big)\\ &=& \mathop{\mathbb P} ( A \cap E ) + \mathop{\mathbb P}( A \cap \overline E )\\ &=& \mathop{\mathbb P} ( A ~|~ E ) \mathop{\mathbb P}(E) + \mathop{\mathbb P}( A ~|~ \overline E )\mathop{\mathbb P}(\overline E ). \end{array}$

Tal fato é um caso particular do seguinte resultado.

Exemplo 21 (Monty Hall revisitado) Se o jogador não troca de porta, ele acerta o carro com probabilidade de acertar uma dentre três portas, i.e., ${1/3}$ . Se o jogador troca de porta, então consideremos os eventos ${ A \equiv \textrm{``ganha o carro''}}$ e ${ E \equiv \textrm{``acerta na escolha inicial''}. }$ Então ${\mathop{\mathbb P}(E)=1/3}$ , ${\mathop{\mathbb P}(A~|~ E)=0}$ e ${\mathop{\mathbb P}(A~|~\overline{E})=1}$ . Pela lei da probabilidade total

$\displaystyle \mathop{\mathbb P}(A) =\mathop{\mathbb P}(A~|~E)\mathop{\mathbb P}(E) + \mathop{\mathbb P}(A~|~\overline{E}) \mathop{\mathbb P}(\overline{E}) =\frac 23$

portanto, é melhor trocar de porta.

Teorema da probabilidade total — caso geral. Seja ${\{E_1,E_2,\dots,E_n\}}$ uma partição de ${\Omega}$ por eventos com ${0<\mathop{\mathbb P}(E_i)<1}$ para todo ${i}$ . Para qualquer evento ${A}$

$\mathop{\mathbb P}(A) = \sum_{i=1}^n \mathop{\mathbb P} (E_i \cap A) = \sum_{i=1}^n \mathop{\mathbb P} (A ~|~ E_i) \mathop{\mathbb P}(E_i).$

Exemplo 22 Uma fábrica de sorvete compra galões de leite de 3 fazendas diferentes.

A fazenda ${F_1}$ entrega todo dia ${20\%}$ do leite usado e uma inspeção revelou que ${20\%}$ desse leite estava adulterado.
A fazenda ${F_2}$ entrega ${30\%}$ do leite usado e a inspeção revelou que ${5\%}$ estava adulterado.
A fazenda ${F_3}$ entrega ${50\%}$ do leite usado, ${2\%}$ adulterado.

Os galões são indistinguíveis. Um é escolhido ao acaso. Qual a probabilidade do evento

${A\equiv}$ “ter leite adulterado”?

O espaço amostral ${\Omega}$ representa os galões de leite e pode ser particionado como ${\Omega = F_1 \cup F_2 \cup F_3}$ . A inspeções nos fornecem as probabilidades

$\displaystyle \mathop{\mathbb P}(A~|~F_1)=0{,}2,\;\; \mathop{\mathbb P}(A~|~F_2)=0{,}05 \;\; \text{ e }\;\;\mathop{\mathbb P}(A~|~F_3)=0{,}02$

usando o teorema da probabilidade total determinamos

$\displaystyle \mathop{\mathbb P}(A) = \mathop{\mathbb P}(A~|~F_1)\mathop{\mathbb P}(F_1)+ \mathop{\mathbb P}(A~|~F_2)\mathop{\mathbb P}(F_2) + \mathop{\mathbb P}(A~|~F_3)\mathop{\mathbb P}(F_3)=0{,}06504065.$

Agora, dado que a amostra de leite está adulterada, qual é a probabilidade de ter sido escolhida da fazenda F1?

$\displaystyle \begin{array}{rcl} \mathop{\mathbb P} (F_1 ~|~ A) &=& \frac{\mathop{\mathbb P}(F_1\cap A)}{\mathop{\mathbb P}(A)} \qquad\qquad \textrm{ por defini\c c\~ao} \\ &=& \frac{\mathop{\mathbb P}(A ~|~ F_1)\mathop{\mathbb P}(F_1)}{\mathop{\mathbb P}(A)} \hfill \qquad \textrm{ pela regra do produto}\\ &=& \frac{0{,}2 \cdot 0{,}2}{0{,}06504065} = 0{,}615. \end{array}$

Suponha que probabilite é uma doença rara que afeta apenas ${0{,}1\%}$ da população, e que existe um teste para detectar probabilite e que não é perfeito: há ${3\%}$ de falsos positivos e ${2\%}$ de falsos negativos. Dado que o teste para um determinado paciente deu positivo, qual é a probabilidade que ele tenha de fato a doença? A lenda diz que a maioria dos médicos respondem ${97\%}$ sem pestanejar, já que há ${3\%}$ de falsos positivos. Essa justificativa está errada. Os eventos de interesse são

${B\equiv}$ “o exame deu positivo” e ${A\equiv}$ “tem probabilite”

a probabilidade de ter a doença é ${\mathop{\mathbb P}(A)= 0{,}001}$ , a probabilidade de um falso positivo é ${\mathop{\mathbb P}( B ~|~ \overline A) = 0{,}03}$ e a de um falso negativo é ${\mathop{\mathbb P}( \overline B ~|~ A)=0{,}02}$ . Queremos determinar ${\mathop{\mathbb P}( A ~|~ B )}$ .

Da definição de probabilidade condicional, se ${A}$ e ${B}$ são eventos com probabilidade positiva então

$\displaystyle \mathop{\mathbb P}(A~|~B) = \frac{\mathop{\mathbb P}(A \cap B)}{\mathop{\mathbb P}(B)}=\frac{\mathop{\mathbb P}(B~|~A)\mathop{\mathbb P}(A)}{\mathop{\mathbb P}(B)}.$

Usando o teorema da probabilidade total para ${B}$ com a partição ${\{A,\overline A\}}$ temos

$\displaystyle \mathop{\mathbb P}(A~|~B) = \frac{\mathop{\mathbb P}(B~|~A)\mathop{\mathbb P}(A)}{\mathop{\mathbb P}(B)} = \frac{\mathop{\mathbb P}(B~|~A)\mathop{\mathbb P}(A)}{\mathop{\mathbb P}(B~|~A)\mathop{\mathbb P}(A) + \mathop{\mathbb P}(B~|~\overline A)\mathop{\mathbb P}(\overline A)}.$

Logo

$\displaystyle \begin{array}{rcl} \mathop{\mathbb P}(A~|~B) = \frac{0{,}98\cdot 0{,}001}{0{,}98\cdot 0{,}001 + {0{,}03}\cdot 0{,}999}= 0{,}031663974 \end{array}$

a chance de ter a doença dado que o teste foi positivo é ligeiramente menor que ${3,2\%}$ , ou seja, tal teste é inútil.

— Teorema de Bayes —

A dedução feita acima pode ser facilmente generalizada para provar o seguinte.

Teorema 12 (Teorema de Bayes) Sejam ${A_1,A_2,\dots,A_m}$ eventos que particionam ${\Omega}$ e ${B\subset \Omega}$ com todos eventos de probabilidade positiva. Para todo ${1\leq j\leq m}$

${\mathop{\mathbb P}(A_{j}~|~B)= \frac{\mathop{\mathbb P}(B~|~A_{j})\mathop{\mathbb P}(A_{j})} {\sum_{i=1}^{m}\mathop{\mathbb P}(B~|~A_{i})\mathop{\mathbb P}(A_{i})}}.$

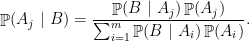
Exemplo 23 Um teste para H1N1 tem 97% de chance de responder certo. Se uma pessoa tem resultado positivo (denotado por “ ${\mathrm{teste}+}$ ”), então ela pode estar “ ${\mathrm{doente}}$ ” ou “ ${\mathrm{nao-doente}}$ ”; o que podemos concluir se sabemos que 60% da população que fica doente?

Usando o teorema de Bayes

$\displaystyle \mathop{\mathbb P} (\mathrm{doente}~|~ \mathrm{teste+}) =$

$\displaystyle \frac{\mathop{\mathbb P}(\mathrm{teste+~|~doente}) \mathop{\mathbb P}(\mathrm{doente})} {\mathop{\mathbb P}(\mathrm{teste+}~|~\mathrm{doente})\mathop{\mathbb P}(\mathrm{doente})+ \mathop{\mathbb P}(\mathrm{teste+}~|~\mathrm{nao-doente})\mathop{\mathbb P}(\mathrm{nao-doente})} =$

$\displaystyle \frac{0{,}97\cdot 0{,}6}{0{,}97\cdot 0{,}6 + 0{,}03\cdot 0{,}4}$

logo a probabilidade é ${0{,}979798}$ .

Exemplo 24 Temos 3 moedas e apenas uma delas, não sabemos qual, é desbalanceada; qualquer uma é a desbalanceada com mesma probabilidade. Essa moeda desbalanceada resulta cara com probabilidade 2/3. Consideremos os eventos ${E_i\equiv}$ definidos por “a i-ésima moeda é a desbalanceada”; logo ${\mathop{\mathbb P}(E_i)=1/3}$ .

Realizamos lançamento de cada uma delas resulta em ${(\mathrm{Ca}}$ , ${\mathrm{Ca}}$ , ${\mathrm{Co})}$ . Consideremos o evento ${B\equiv}$ “o resultado dos lançamentos é ${\mathrm{Ca,~ Ca,~Co}}$ ”.

$\displaystyle \begin{array}{rcl} \mathop{\mathbb P}(B~|~E_1) &=& \frac 23 \times \frac 12 \times \frac 12 = \frac 16\\ \mathop{\mathbb P}(B~|~E_2) &=& \frac 12 \times \frac 23 \times \frac 12 = \frac 16\\ \mathop{\mathbb P}(B~|~E_3) &=& \frac 12 \times \frac 12 \times \frac 13 =\frac 1{12} \end{array}$

Usando o Teorema de Bayes

$\displaystyle \mathop{\mathbb P}(E_1~|~B) = \frac{\mathop{\mathbb P}(B~|~E_1)\mathop{\mathbb P}(E_1)}{\mathop{\mathbb P}(B~|~E_1)\mathop{\mathbb P}(E_1)+\mathop{\mathbb P}(B~|~E_2)\mathop{\mathbb P}(E_2) +\mathop{\mathbb P}(B~|~E_3)\mathop{\mathbb P}(E_3)}= \frac 25$

lembremos que ${\mathop{\mathbb P}(E_1) = 1/3}$ , logo “aprendemos mais” sobre as moedas depois do lançamento. Também, ${\mathop{\mathbb P}(E_2|~B) = 2/5}$ mas ${\mathop{\mathbb P}(E_3~|~B) = 1/5}$ .

Exercicio 35 Um pais extremamente democrático mantém três prisioneiros sem qualquer acusação na prisão de Guantánamo. São eles: Said, Osama e Ayman. O carcereiro diz a eles que um será libertado e os outros serão executados, mas não lhe foi permitido dizer o que acontecerá a cada um. Said avalia que ele tem chance de ${1/3}$ de escapar e pensou em perguntar em segredo ao carcereiro qual dos outros prisioneiros seria executado; em seguida avaliou que se o carcereiro respondesse o Osama, por exemplo, então a chance dele escapar passaria a ser ${1/2}$ pois seria ou ele e Osama, ou ele e Ayman. Essa avaliação está correta?

— Independência —

Vimos nos exemplos acima, como o exemplo 24, que o conhecimento da ocorrência de um evento ${E}$ afeta a probabilidade de ocorrência de ${A}$ , a probabilidade ${\mathop{\mathbb P}(A~|~E)}$ não é, em geral, igual a ${\mathop{\mathbb P}(A)}$ . Quando esse não é o caso, dizemos que os eventos são independentes.

Os eventos ${A}$ e ${B}$ são ditos independentes se

${\mathop{\mathbb P}(A\cap B)=\mathop{\mathbb P}(A)\mathop{\mathbb P}(B)}$ .

Se os eventos têm probabilidade positiva então decorre da definição acima que a independência de ${A}$ e ${B}$ equivale a ${\mathop{\mathbb P}(A~|~B)=\mathop{\mathbb P}(A)}$ e ${\mathop{\mathbb P}(B~|~A)=\mathop{\mathbb P}(B)}$ .

Uma coleção de eventos ${E_{1},E_2,\dots,E_{n},\dots}$ é dita independente se para toda subcoleção finita ${E_{i_{1}},E_{i_{2}}, \cdots,E_{i_{k}}}$ vale que

$\mathop{\mathbb P}\left(\bigcap_{\ell=1}^{k} E_{i_{\ell}}\right)= \mathop{\mathbb P}(E_{i_{1}})\mathop{\mathbb P}(E_{i_{2}}) \cdots \mathop{\mathbb P}(E_{i_{\ell}})$ .

qualquer que seja ${k\in\{2,3,\dots\}}$ .

Exemplo 25 Consideremos o espaço amostral com 9 elementos dado pelas 6 permutações das letras ${a,b,c}$ mais as 3 ternas ${(a,a,a)}$ , ${(b,b,b)}$ e ${(c,c,c)}$ , cada uma com probabilidade ${1/9}$ . Seja ${E_i}$ o evento “a coordenada ${i}$ é a”. Então ${\mathop{\mathbb P}(E_i)= 1/3}$ e ${\mathop{\mathbb P}(E_i \cap E_j) = 1/9}$ para ${i\neq j}$ , portanto os eventos são 2-a-2 independentes, mas não são independentes pois, por exemplo, a ocorrência de ${E_1}$ e ${E_3}$ implica na ocorrência de ${E_2}$ ; de fato, ${\mathop{\mathbb P}(E_1\cap E_2\cap E_3) = 1/9}$ .

Exemplo 26 Consideremos três lançamentos de uma moeda equilibrada e os eventos
${E_{12} \equiv}$ “o resultado do primeiro e do segundo coincidem”
${E_{13}\equiv}$ “o resultado do primeira e do terceiro coincidem” e
${E_{23}\equiv}$ “o resultado do segundo e do terceiro coincidem”.

$\displaystyle \mathop{\mathbb P}(E_{12})=\mathop{\mathbb P}(E_{13})=\mathop{\mathbb P}(E_{23})= \frac 12$

Os eventos são 2-a-2 independentes,

$\displaystyle \mathop{\mathbb P}\left( E_{12}\cap E_{13} \right)= \mathop{\mathbb P}\left(\{ \mathrm{(Ca,Ca,Ca),(Co,Co,Co)}\}\right) = \frac 14.$

Analogamente, para ${E_{12}\cap E_{23}}$ e ${E_{13}\cap E_{23}}$ , entretanto, esses eventos não são independentes pois

$\displaystyle \frac 14 = \mathop{\mathbb P}( E_{12}\cap E_{13}\cap E_{23}) \quad\neq \quad \mathop{\mathbb P}( E_{12}) \mathop{\mathbb P}( E_{13}) \mathop{\mathbb P}(E_{23})= \frac 18$

Exemplo 27 Tomemos ${\Omega = \{1,2,3,4,5,6,7,8,9,10\}}$ com a probabilidade clássica, e consideremos os eventos ${A=\{2,3,4,5,6\}}$ , ${B=\{4,5,6,7,8,9\}}$ , ${C=\{2,3,4,5,6,7,8,9,10\}}$ e ${D=\{1,7,8,9\}}$ . Temos ${\mathop{\mathbb P}(A~|~B) = 1/2 =\mathop{\mathbb P}(A)}$ e ${\mathop{\mathbb P}(B~|~A) = 3/5 = \mathop{\mathbb P}(B)}$ . Portanto ${A}$ e ${B}$ são eventos independentes.

Agora, ${\mathop{\mathbb P}(A~|~C) = 5/9 > \mathop{\mathbb P}(A)}$ de modo que ${A}$ e ${C}$ não são independentes. Também, ${\mathop{\mathbb P}(B~|~C) = 2/3 > \mathop{\mathbb P}(B)}$ .

Ainda, ${\mathop{\mathbb P}(A~|~D) = 0 < \mathop{\mathbb P}(A)}$ de modo que ${A}$ e ${D}$ não são independentes .Também, ${\mathop{\mathbb P}(B~|~D) = 3/4 > \mathop{\mathbb P}(B)}$ e ${\mathop{\mathbb P}(C~|~D) = 3/4 < \mathop{\mathbb P}(C)}$ .

Exemplo 28 Um dado de 4 faces tem uma face de cor Azul, uma face de cor Branca, uma face de cor Cinza, e uma face com as três cores, todas com a mesma probabilidade de ocorrência num lançamento. Representamos o resultado de um lançamento pelas letras ${A,B,C}$ . Então ${\mathop{\mathbb P}(A)= \mathop{\mathbb P}(B)= \mathop{\mathbb P}(C)= 1/2}$ pois cada cor aparece em 2 das 4 faces. Também ${\mathop{\mathbb P}(A~|~B)= \mathop{\mathbb P}(B~|~C) = \mathop{\mathbb P}(C~|~A) = \mathop{\mathbb P}(B~|~A) = \mathop{\mathbb P}(C~|~B) = \mathop{\mathbb P}(A~|~C) =1/2}$ , portanto, os eventos são 2-a-2 independentes. Entretanto ${\mathop{\mathbb P}(A~|~B\cap C)=1}$ portanto os eventos não são independentes.

Exercicio 36 Mostre que se ${A}$ e ${B}$ são eventos independentes, então são eventos independentes: ${(a)}$ ${\overline A}$ e ${\overline B}$ ; ${(b)}$ ${A}$ e ${\overline B}$ ; ${(c)}$ ${\overline A}$ e ${B}$ .

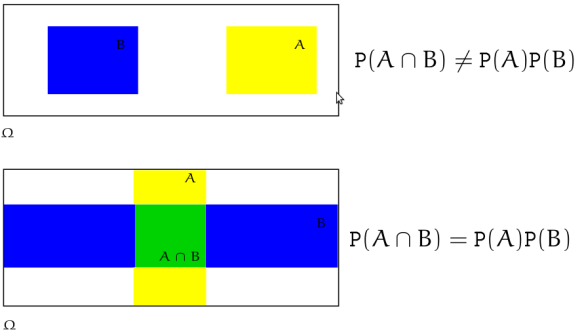
Independência ${\times}$ exclusão: Não confunda esses termos.

Na figura de cima os eventos são mutuamente exclusivos mas não independentes. Na figura de baixo os eventos são independentes mas não mutuamente exclusivos.

Problema: Uma urna contém seis bolas, digamos que três são vermelhas e três azuis. Uma dessas bolas, chamemos-a bola ${A}$ , é selecionada ao acaso removida permanentemente da urna sem que a sua cor seja revelada para um observador. Esse observador pode agora retirar bolas sucessivamente, uma de cada vez, de forma aleatória e com reposição um número pré-determinado de vezes. O objetivo dessa experimentação é a formar uma ideia aproximada da proporção de bolas vermelhas e azuis que permaneceram na urna após a retirada da bola ${A}$ .

Pedro, na condição de observador, retirou uma bola seis vezes, e todos resultados foram bolas vermelhas. Paula retirou uma bola da urna 600 vezes, 303 vezes foram bolas vermelhas e 297 vezes bolas azuis. Claramente, ambos tendem a prever que a bola ${A}$ é, provavelmente, azul. Qual deles, se é que algum, tem a evidência empírica mais forte de sua previsão?

— Mais exemplos —

A seguir, apresentamos mais exemplos a respeito do tema apresentado acima.

Exemplo 30 Suponhamos que o @alunodaufabc está em dúvida entre matricular-se em Física Quântica e Introdução à Probabilidade e à Estatística cujos horários de aula coincidem. Ele estima que a probabilidade de passar com ${A}$ em FQ é ${1/2}$ e a de passar com ${A}$ em IPE é ${2/3}$ . Se ele usar uma moeda para escolher a disciplina, qual é a probabilidade de passar com ${A}$ em IPE? Se ${A}$ representa “passar com ${A}$ ” e ${P}$ representa “cursar IPE”

$\displaystyle \mathop{\mathbb P}(P\cap A) = \mathop{\mathbb P}(A~|~P)\mathop{\mathbb P}(P) = \frac 23 \cdot \frac 12= \frac 13.$

Exemplo 31 Um investigador de polícia está ${60\%}$ convencido da culpa de um determinado suspeito. No decorrer da investigação uma nova evidência na cena do crime prova que o criminoso tinha uma determinada característica, seu pé-direito tem seis dedos. Sabe-se que ${20\%}$ da população tem seis dedos no pé direito. Dado que o suspeito tem seis dedos no pé direito, qual é o grau de convencimento do investigador?

Representemos por ${H}$ o evento “suspeito culpado” e por ${E}$ o evento “tem seis dedos no pé direito” e temos pelo Teorema de Bayes que

$\displaystyle \mathop{\mathbb P} (H~|~E) = \frac{\mathop{\mathbb P}(E~|~H)\mathop{\mathbb P}(H)} { \mathop{\mathbb P}(E~|~H)\mathop{\mathbb P}(H) + \mathop{\mathbb P}(E~|~\overline H)\mathop{\mathbb P}(\overline H)} = \frac{1\cdot 0{,}6}{1\cdot 0{,}6+0{,}2\cdot 0{,}4} = 0{,}882352941$

ou seja, o grau de convencimento agora é ${88,2\%}$ .

Exemplo 32 No contexto do exemplo anterior, se ${H}$ é uma hipótese e ${E}$ uma evidência então

$\displaystyle \mathop{\mathbb P} (H~|~E) = \frac{\mathop{\mathbb P}(E~|~H)\mathop{\mathbb P}(H)} { \mathop{\mathbb P}(E)} \qquad\textrm{ e }\qquad \mathop{\mathbb P} (\overline H~|~E) = \frac{\mathop{\mathbb P}(E~|~\overline H)\mathop{\mathbb P}(\overline H)}{\mathop{\mathbb P}(E)}$

portanto

$\displaystyle \frac{\mathop{\mathbb P} (H~|~E)}{\mathop{\mathbb P} (\overline H~|~E)} = \frac{\mathop{\mathbb P} ( H ) }{\mathop{\mathbb P} (\overline H)} \cdot \frac{\mathop{\mathbb P}(E~|~H)}{\mathop{\mathbb P}(E~|~\overline H)} \ \ \ \ \ (30)$

onde

$\displaystyle \frac{\mathop{\mathbb P} ( H ) }{\mathop{\mathbb P} (\overline H)} \qquad\textrm{ e }\qquad \frac{\mathop{\mathbb P} (H~|~E)}{\mathop{\mathbb P} (\overline H~|~E)}$

quantificam, respectivamente, quanto provável é a ocorrência de ${H}$ com relação a não ocorrência de ${H}$ , e quão mais provável é a ocorrência de ${H}$ com relação a não ocorrência após a introdução da evidência ${E}$ .

Portanto, se a ${\mathrm{hipotese}}$ é culpa e a ${\mathrm{evidencia}}$ é uma característica do criminoso, no exemplo anterior temos

$\displaystyle \frac{\mathop{\mathbb P}(E~|~H)}{\mathop{\mathbb P}(E~|~\overline H)} = \frac 1{0{,}2} = 5$

ou seja, após a nova evidência a culpa é 5 vezes mais provável.

Exemplo 33 (Falácia do promotor) Essa falácia geralmente resulta em assumir que a probabilidade prévia de que uma evidência condenaria um membro escolhido aleatoriamente da população é igual à probabilidade de que ela condenaria o réu. Por exemplo, você ganha na loteria, mas é acusado de fraude. No julgamento o promotor afirma que ganhar na loteria sem trapacear é extremamente improvável portanto é igualmente extremamente improvável que você seja inocente. Isso desconsidera que a probabilidade de qualquer outra pessoa ganhe na loteria é igualmente pequena. A confusão típica é, usando a linguagem dos tribunais, que

se

$\displaystyle \mathop{\mathbb P} (\textrm{evid\^encia~comprovada}~|~\textrm{inoc\^encia~do~suspeito})$

é pequena, então

$\displaystyle \mathop{\mathbb P} (\textrm{inoc\^encia~do~suspeito}~|~\textrm{evid\^encia~comprovada})$

é pequena.

De fato, essas probabilidade podem ser muito diferentes como mostramos a seguir. No caso de teste de DNA para identificar criminosos, dependendo do número de locus considerado na análise, é possível que a frequência de determinado padrão seja da ordem de 1 em 1 milhão [Technology in Forensic Science]. O erro comum é a confusão resultante de tomar por aproximadamente igual

a probabilidade que a amostra de DNA de uma outra pessoa (não o criminoso) case com o padrão do DNA descoberto na cena do crime, dado que a pessoa é inocente;
a probabilidade que a pessoa é inocente dado que seu DNA casa com o padrão do DNA descoberto na cena do crime.

A primeira é a probabilidade atestada por um perito em exame de DNA; quando um teste de DNA atesta que “a probabilidade é de 1 em 100 milhões que o DNA da cena do crime case como DNA do suspeito” isso significa que “a chance do casamento de padrões entre o DNA na cena do crime e do DNA do acusado é de 1 em 100 milhões, se o acusado é inocente e não é parente do criminoso”, pondo de outro modo ${P (\textrm{evid\^encia}~|~\textrm{inoc\^encia})}$ é pequena. A segunda probabilidade, descrita acima, é a que interessa ao promotor para poder acusar sem erro o suspeito e uma vez que o resultado positivo é certo ${(\mathop{\mathbb P} (\textrm{inoc\^encia}~|~\textrm{evid\^encia}))}$ , se o acusado deixou a amostra de DNA na cena do crime então

$\displaystyle \frac{\mathop{\mathbb P} (\textrm{evid\^encia}~|~\textrm{culpa})} {\mathop{\mathbb P} (\textrm{evid\^encia}~|~\textrm{inoc\^encia})}= 100 \textrm{ milh\~oes}$

ou seja, independentemente da chance a priori de culpa, a evidência do DNA torna a probabilidade de culpa 100 milhões de vezes maior que a de inocência, de acordo com a equação (30) acima

$\displaystyle \displaystyle \frac{\mathop{\mathbb P} (\textrm{culpa}~|~\textrm{evid\^encia})} {\mathop{\mathbb P} (\textrm{inoc\^encia}~|~\textrm{evid\^encia})} = 100.000.000\frac{\mathop{\mathbb P} (\textrm{culpa})} {\mathop{\mathbb P} (\textrm{inoc\^encia})}.$

Exemplo 34 O seguinte relato foi extraído de uma reportagem da revista TIME de sexta-feira, 8 de janeiro de 1965. “Por volta do meio-dia, em um dia de Junho último, uma mulher idosa foi assaltada em um beco em San Pedro, na Califórnia. Pouco depois, uma testemunha viu uma garota loira com rabo de cavalo saindo do beco e entrando em um carro amarelo conduzido por um negro com barba e bigode. A polícia prendeu e Janet e Malcolm Collins, um casal que que encaixava na descrição física dada pela testemunha e que possuía um Lincoln amarelo.”

Ao apresentar o caso o promotor, que teve acessoria de um professor de matemática local, salientou a baixa probabilidade de haver casais como os Collins em San Pedro, em um carro amarelo pois

probabilidade de carro amarelo = 1 / 10;
probabilidade de homem com bigode = 1 / 4;
probabilidade de mulher com rabo de cavalo = 1 / 10;
probabilidade mulher tem cabelo loiro = 1 / 3;
probabilidade de homem negro com barba = 1 / 10;
probabilidade de casal inter-racial = 1 / 1000;

Multiplicando todos esses valores leva a um valor de 1 em 12 milhões para a probabilidade de haver um casal com as mesmas características de Janet e Malcolm Collins. O casal acabou sendo condenado. Qual é o problema desse argumento?

Veja este link se quiser mais detalhes sobre as considerações legais do processo e o desdobramento. Há vários casos reais de uso incorreto de probabilidade num julgamento, veja os casos Lucia de Berk, Kevin Sweeney, Sally Clark.

Exemplo 35 As seguradoras de automóveis classificam motoristas em propensos a acidentes e não propensos a acidentes; estimam que os propensos são ${30\%}$ da população. As estatísticas mostram que os propensos se envolvem em acidente no período de um ano com probabilidade ${0{,}4}$ e os não propensos com probabilidade ${0{,}2}$ . Seja ${A}$ o evento definido pelos motoristas propensos. Então, a probabilidade de um novo segurado se envolver em acidente em um ano é

$\displaystyle \mathop{\mathbb P}(A_1) = \mathop{\mathbb P}(A_1~|~A)\mathop{\mathbb P}(A) + \mathop{\mathbb P}(A_1~|~\overline A)\mathop{\mathbb P}(\overline A) = 0{,}4\cdot 0{,}3+0{,}2\cdot0{,}7=0{,}26$

se um novo segurado se envolve em acidente nesse prazo, a probabilidade dele ser propenso é

$\displaystyle \mathop{\mathbb P}(A~|~A_1) = \frac{\mathop{\mathbb P}(A_1~|~A)\mathop{\mathbb P}(A)}{\mathop{\mathbb P}(A_1)} = \frac{0{,}3\cdot0{,}4}{0{,}26}= \frac 6{13}.$

Qual a probabilidade de ocorrer um acidente no 2º ano dado que tenha acidentado no 1º ano de contrato? Definimos a medida de probabilidade, sobre os mesmos evento, ${{\mathbb Q}(\cdot) = \mathop{\mathbb P}(\cdot~|~A_1)}$ (veja o exercício 34). Dessa forma, pela Lei de Probabilidade Total

$\displaystyle {\mathbb Q}(A_2) = {\mathbb Q}(A_2 ~|~A) {\mathbb Q}(A) + {\mathbb Q}(A_2 ~|~\overline A) {\mathbb Q}(\overline A)$

onde, por definição,

$\displaystyle {\mathbb Q}(A_2~|~A) = \frac{{\mathbb Q}(A_2\cap A)}{{\mathbb Q}(A)}= \frac{\mathop{\mathbb P}(A_2\cap A~|~A_1)}{\mathop{\mathbb P}(A~|~A_1)}.$

Exercicio 38 Mostre que ${{\mathbb Q}(A_2 ~|~A) = \mathop{\mathbb P}(A_2 ~|~A\cap A_1)}$ .

Assumiremos que ${A_1}$ e ${A_2}$ são condicionalmente independentes dado ${A}$ , ou seja,

$\displaystyle \mathop{\mathbb P}(A_2 ~|~A\cap A_1) = \mathop{\mathbb P}(A_2 ~|~ A)$

que equivale a ${\mathop{\mathbb P}(A_2 \cap A_1~|~A) = \mathop{\mathbb P}(A_1~|~A)\mathop{\mathbb P}(A_2 ~|~ A)}$ .

Portanto, ${ {\mathbb Q}(A_2 ~|~A) =0{,}4}$ e temos que

$\displaystyle \begin{array}{rcl} {\mathbb Q}(A_2) &=(A_2 ~|~A) {\mathbb Q}(A) + {\mathbb Q}(A_2 ~|~\overline A) {\mathbb Q}(\overline A)\\ \mathop{\mathbb P}(A_2~|~A_1) &=& \mathop{\mathbb P}(A_2 ~|~A) \mathop{\mathbb P}(A~|~A_1) + \mathop{\mathbb P}(A_2 ~|~\overline A) \mathop{\mathbb P}(\overline A~|~A_1)\\ \mathop{\mathbb P}(A_2~|~A_1) &=& 0{,}4\cdot \frac 6{13}+0{,}2\cdot\frac 1{13}=0{,}29. \end{array}$

Exemplo 36 (Filtros bayesiano anti-spam) A abordagem Bayesiana para filtrar mensagens (uma das ferramentas do spamassassin, por exemplo) foi ideia de Paul Graham que descreve aqui como eles funcionam. Abaixo daremos uma explicação resumida e formal de como usar o teorema de Bayes na classificação de mensagens que são spam.

O espaço amostral é dado por ${\{0{,}1\}^n}$ de modo que cada coordenada indica se uma mensagem tem (representado por ${1}$ ) ou não tem (representado por ${0}$ ) uma determinada característica e a primeira coordenada de uma ${n}$ -nupla, especificamente, é ${1}$ se a mensagem é spam e ${0}$ caso, contrário.

Assim o evento ${S}$ dado por ${\{1\}\times \{0,1\}^{n-1}}$ é o evento é spam e ${\overline{S}=\{0\}\times\{0,1\}^{n-1}}$ é o evento não é spam.

Denotamos por ${C_i}$ , ${ i\geq 2}$ , o evento “tem a característica ${i}$ ” que corresponde a todos os vetores cuja ${i}$ -ésima coordenada é ${1}$ .

Vamos assumir que as características ${2,3\dots,n}$ são independentes condicionalmente

$\displaystyle \mathop{\mathbb P} \left( \bigcap_{i\in I}C_i \big| S \right) = \prod_{i\in I} \mathop{\mathbb P} \left( C_i \big| S \right)$

$\displaystyle \mathop{\mathbb P} \left(\bigcap_{i\in I}C_i \big|\overline{S}\right)= \prod_{i\in I} \mathop{\mathbb P}\left(C_i\big|\overline{S}\right)$

para todo ${I\subseteq \{2,3,\dots,n\}}$ (pode não ser uma hipótese muito realista. Por exemplo, se a característica ${2}$ é conter a palavra watch e a característica ${3}$ é conter a palavra replica então um email que contém replica tem muito mais chance de conter watch; o meu endereço de email recebe várias dessas mensagens que anunciam réplicas de relógios caros e watch só aparece nesses spams; esse pode não ser o caso de um relojoeiro num país de língua inglesa).

Pelo teorema de Bayes

$\displaystyle \mathop{\mathbb P} \left(S\Big|\bigcap_{i\in I}C_i\right)= \frac{\prod_{i\in I} \mathop{\mathbb P}(S|C_i)}{\prod_{i\in I}\mathop{\mathbb P}(S|C_i) +\big(\mathop{\mathbb P}(S)/\mathop{\mathbb P}(\overline{S})\big)^{|I|-1}\prod_{i\in I}\mathop{\mathbb P}(\overline{S}|C_i)}. \ \ \ \ \ (31)$

(Dica: use o teorema de Bayes com ${S}$ , ${\overline{S}}$ e ${\bigcap_i C_i}$ .)

Agora, suponha que temos ${100}$ mensagens, ${50}$ spams e ${50}$ não spams. O trabalho inicial é definir características das mensagens que são spams das que não são. Por exemplo, nas minhas mensagens muitos dos spams têm a palavra watch enquanto que muitos dos não spams têm a palavra reunião; a maioria das mensagens têm a palavra a, tantos spams quanto não spams, logo a não deve ser uma característica levada em consideração.

Para a característica ${ i}$ , seja ${ k_i}$ a quantidade de spams que têm a característica ${ i}$ e seja ${ \ell_i}$ a quantidade de não spams que têm a característica ${ i}$ ; definimos ${\mathop{\mathbb P} (C_i | S) = \frac{k_i}{50}}$ e ${\mathop{\mathbb P} (C_i |\overline{S}) = \frac{\ell_i}{50}}$ e pelo teorema de Bayes,

$\displaystyle \mathop{\mathbb P} (S|C_i) = \frac{\mathop{\mathbb P}\left(C_i|S\right)\mathop{\mathbb P}(S)}{\mathop{\mathbb P}(C_i|S)\mathop{\mathbb P}(S) +\mathop{\mathbb P}(C_i|\overline{S})\mathop{\mathbb P}(\overline{S})} =\frac{k_i\mathop{\mathbb P}(S)}{k_i\mathop{\mathbb P}(S)+\ell_i\mathop{\mathbb P}(\overline{S})}.$

Recebida uma mensagem, filtramo-lá para determinar suas características, digamos ${C_i}$ com ${i\in I}$ , e (31) determina a probabilidade dessa mensagem ser spam.

Exemplo 37 Com que probabilidade uma máquina que está funcionando no instante ${t_0}$ continuará funcionando até o instante ${t_0+t}$ supondo que essa probabilidade dependa somente do comprimento do intervalo ${(t_0,t_0+t)}$ , supondo que a probabilidade com que a máquina pare durante um intervalo de comprimento ${\Delta t}$ proporcional a ${\Delta t}$ e supondo que os eventos que consistem da máquina parar durante intervalos disjuntos são independentes?

Se ${p(t)}$ é a probabilidade procurada. A probabilidade da máquina parar num intervalo de tempo de tamanho ${\Delta t}$ é ${1-p(\Delta t) = \alpha \Delta t}$ , para alguma constante fixa ${\alpha >0}$ . A probabilidade com que uma máquina que está funcionando no instante ${t_0}$ continuará funcionando até o instante ${t_0+t+\Delta t}$ é ${p(t+\Delta t)}$ e pela independência assumida ${p(t+\Delta t) = p(t)\cdot p(\Delta t)}$ logo ${p(t+\Delta t) = p(t)(1 - \alpha \Delta t)}$ de modo que

$\displaystyle \frac{p(t+\Delta t) - p(t)}{\Delta t} = -\alpha p(t)$

que, passando ao limite quando ${\Delta t \rightarrow 0}$ , resulta em

$\displaystyle \frac{\mathrm{d}}{\mathrm{d}t} = - \alpha p(t)$

donde temos ${p(t) = C \mathrm{e}^{- \alpha t}}$ para alguma constante ${C}$ . De ${p(0)=1}$ deduzimos que ${C=1}$ .

— Paradoxo de Simpson —

É um paradoxo estatístico descrito por Edward Simpson em 1951 e George Udny Yule em 1903, em que o sucesso em grupos parece ser revertida quando os grupos são combinados. Esse resultado é surpreendente e frequentemente encontrado na prática, especialmente nas ciências sociais e as estatísticas médicas. Há vários casos conhecidos e bem estudados, vamos começar com uma simplificação de um caso conhecido.

200 em 1000 homens e 150 em 1000 mulheres escolhem cursar Economia em uma universidade P. Se o curso for na universidade Q os números são 30 em 100 homens e 1000 em 4000 mulheres. Temos as seguintes proporções por sexo

	Homem	Mulher
P	${0{,}2~(200/1000)}$	${0{,}15~(150/1000)}$
Q	${0{,}3~(30/100)}$	${0{,}25~(1000/4000)}$
Ambas	${0{,}21~(230/1100)}$	${0{,}23~(1150/5000)}$

Se consideremos os dois cursos em conjunto a proporção de homens é ${\approx 0{,}21}$ e a de mulheres ${0{,}23}$ , ou seja, em conjunto a proporção de mulheres é maior. Outro exemplo é de um estudo sobre dois tratamentos (H e M, não tem relação com sexo) para pedras no rim, em função do tamanhos das pedras (pequenas ou grandes) em quatros grupos de estudo, a seguinte tabela mostra o sucesso dos tratamentos

	H	M
Pequenas	${0{,}93~(81/87)}$	${0{,}87~(234/270)}$
Grandes	${0{,}73~(192/263)}$	${0{,}69~(55/80)}$
Ambos	${0{,}78~(273/350)}$	${0{,}83~(289/350)}$

e o paradoxo é que o tratamento H tem maior taxa de sucesso se consideramos isoladamente as pedras pequenas (0{,}93) ou as pedras grandes (0{,}73), no entanto, no quadro geral o tratamento M tem maior taxa de sucesso (0{,}83).

Em termos gerais, o paradoxo ocorre porque as desigualdades

$\displaystyle \mathop{\mathbb P}(A~|~P\cap H) > \mathop{\mathbb P} (A~|~ P\cap \overline H) \,\text{ e }\, \mathop{\mathbb P}(A~|~ \overline P\cap H) > \mathop{\mathbb P} (A~|~\overline P\cap \overline H) \ \ \ \ \ (32)$

$\displaystyle \mathop{\mathbb P}(A~|~H) < \mathop{\mathbb P}(A~|~ \overline H) \ \ \ \ \ (33)$

são compatíveis.

Veja outro exemplo aqui

— Exercícios —

Mostre que para eventos ${A}$ , ${B}$ e ${C}$ vale
$\displaystyle \mathop{\mathbb P} (A \cap B \cap C) = \mathop{\mathbb P}(A) \mathop{\mathbb P}(B ~|~ A) \mathop{\mathbb P} (C ~|~ A\cap B). \ \ \ \ \ (35)$

Também vale que, se ${D}$ é evento então

$\displaystyle \mathop{\mathbb P} (A \cap B \cap C\cap D) = \mathop{\mathbb P}(A) \mathop{\mathbb P}(B ~|~ A) \mathop{\mathbb P} (C ~|~ A\cap B)\mathop{\mathbb P}(D~|~A\cap B\cap C).$

Assuma que todos os eventos envolvidos tenha probabilidade positiva para que as probabilidades condicionais estejam definidas.
(Regra generalizada do produto) Sejam ${A_2,A_2,\dots,A_n}$ eventos tais que ${\mathop{\mathbb P}(A_1\cap A_2\cap\cdots\cap A_n)>0}$ . Então
$\displaystyle \mathop{\mathbb P}\left(\bigcap_{i=1}^n A_i\right) = \mathop{\mathbb P}(A_1)\prod_{i=2}^{n-1} \mathop{\mathbb P}\left(A_i~\bigg|~\bigcap_{j=1}^{i-1}A_j\right).$
Use (35) pare determinar qual é a probabilidade de ocorrer três reis ao se retirar três cartas ao acaso de um baralho.
O teorema da probabilidade total vale para uma partição enumerável por eventos de ${\Omega}$ , digamos ${\{E_1,E_2,\dots,E_n, \dots\}}$ com ${\mathop{\mathbb P}(E_i)>0}$ para todo ${i}$ ?
No ultimo ano de uma classe com 100 alunos que estão se formando no ensino médio, 42 estudaram matemática, 68 estudaram psicologia, 54 estudaram historia, 22 estudaram matemática e historia, 25 estudaram matemática e psicologia, 7 estudaram historia mas não estudaram matemática nem psicologia, 10 estudaram as três matérias e 8 não estudaram nenhuma. Se um estudante é selecionado ao acaso
(a) qual é a probabilidade que uma pessoa matriculada em psicologia tenha estudado as três matérias;
(b) qual é a probabilidade que uma pessoa não esteja estudando psicologia esteja estudando historia e matemática.
A probabilidade de que um homem casado assista determinado programa de TV é ${0,4}$ e a probabilidade que uma mulher casada é ${0,5}$ . A probabilidade que um homem assista dado que sua mulher assista é ${0,7}$ . Determine a probabilidade de que
(a) um casal assista ao programa; \resp{0,35}
(b) uma esposa assista ao programa, dado que o marido o faça;\resp{0,875}
(c) pelo menos uma pessoa do casal assista ao programa.\resp{0,55}
A probabilidade de que um medico acerte o diagnostico de uma doença é ${0{,}7}$ . Dado que o médico fez um diagnostico incorreto, a probabilidade de que o paciente entre com um processo é ${0{,}9}$ . Qual é a probabilidade de que o médico erre o diagnóstico e seja processado pelo paciente. \resp{0,27}
Um corretor de imóveis tem oito chaves mestras para abrir diversas casas. Somente uma delas abrirá qualquer uma das casas. Se 40% dessas casas são, normalmente, deixadas destrancadas, qual é a probabilidade de que o corretor entre em uma casa específica se ele selecionou três chaves mestras aleatoriamente antes de sair do escritório?
Uma cidade tem dois carros de bombeiros operando independentemente. Cada carro tem probabilidade 0,96 de estar disponível em caso de necessidade.
(a) Qual é a probabilidade de que nenhum carro esteja disponível quando necessário? \resp{0,0026}
(b) Qual é a probabilidade de que algum carro esteja disponível quando necessário? \resp{0,9984}
Um sistema de circuitos é dado na figura abaixo. Assuma que os componentes falham independentemente.

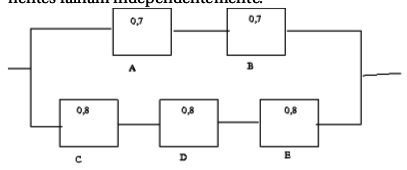
(a) Qual é a probabilidade que o sistema todo funcione?\resp{0,75112}
(b)Dado que o sistema funciona, qual é a probabilidade de que o componente A não esteja funcionando?\resp{0,2045}
Em certa região do país sabe-seque a probabilidade de selecionar um adulto com mais de 40 anos com câncer é 0,05. Se a probabilidade de um médico diagnosticar corretamente uma pessoa com câncer como portadora da doença é 0,78 e a probabilidade de diagnosticar incorretamente uma pessoa sem câncer como sendo portadora da doença é 0,06, qual é a probabilidade de que a pessoa seja diagnosticada com câncer?
No exercício acima, qual é a probabilidade de que a pessoa diagnosticada com câncer realmente tenha a doença?
Suponha que quatro inspetores em uma fabrica e filmes tenham que estampar a data de validade em cada pacote de filme ao final da linha de montagem. João, que estampa 20% dos pacotes, não estampa a data de validade em 1 de cada 20 pacotes; Toni, que estampa 60% dos pacotes, erra uma vez a cada 100 pacotes; Jeff, que estampa 15% dos pacotes, erra uma vez a cada 90 pacotes e Paty que estampa 5% dos pacotes, erra uma vez a cada 200 pacotes. Se um cliente reclame que sua embalagem de filme não contém a data de validade, qual é a probabilidade de que ela tenha sido inspecionada por João?\resp{0,1124}
Considere os seguintes eventos
$\displaystyle A\equiv \textrm{``o rio \'e poluido''}$

$\displaystyle B\equiv \textrm{``uma amostra de \'agua testada detecta polui\c{c}\~ao''}$

$\displaystyle C\equiv \textrm{``a pesca \'e permitida''}$

Assuma ${\mathop{\mathbb P}(A)=0,3}$ , ${\mathop{\mathbb P}(B~|~A)=0,75}$ , ${\mathop{\mathbb P}(B~|~\overline A)=0,2}$ , ${\mathop{\mathbb P}(C~|~A\cap B)=0,2}$ , ${\mathop{\mathbb P}(C~|~\overline{A}\cap B)=0,15}$ , ${\mathop{\mathbb P}(C~|~A\cap \overline B)=0,8}$ e ${\mathop{\mathbb P}(C~|~ \overline A\cap \overline B)=0,9}$ . Determine
1. ${\mathop{\mathbb P}(A\cap B\cap C)}$ ;\resp{0,045}
2. ${\mathop{\mathbb P}(\overline B\cap C)}$ ;\resp{0,564}
3. ${\mathop{\mathbb P}(C)}$ ;\resp{0,63}
4. determine a probabilidade de o rio ser poluído, dado que a pesca é permitida e a amostra testada não detectou poluição.\resp{0,1064}
Mostre que se ${\mathop{\mathbb P}}$ é uma medida de probabilidade e ${E}$ um evento com probabilidade positiva, então ${\mathop{\mathbb P}'}$ dada por ${\mathop{\mathbb P}'(A) = \mathop{\mathbb P}(A~|~E)}$ é uma medida de de probabilidade para os mesmos eventos.
Mostre que se ${A}$ e ${B}$ são eventos independentes, então ${(a)}$ ${\overline A}$ e ${\overline B}$ são eventos independentes; ${(b)}$ ${A}$ e ${\overline B}$ são eventos independentes; ${(c)}$ ${\overline A}$ e ${B}$ são eventos independentes.
Mostre que para eventos ${A}$ , ${B}$ , ${C}$ e ${D}$ são eventos então
$\displaystyle \mathop{\mathbb P} (A \cap B \cap C\cap D) = \mathop{\mathbb P}(A) \mathop{\mathbb P}(B ~|~ A) \mathop{\mathbb P} (C ~|~ A\cap B)\mathop{\mathbb P}(D~|~A\cap B\cap C).$

Assuma que todos os eventos envolvidos tenha probabilidade positiva para que as probabilidades condicionais estejam definidas.
Seja ${\Omega = \{1,2,\dots,p\}}$ para ${p}$ primo e ${\mathop{\mathbb P}(A) = |A|/p}$ , para todo ${A\subset \Omega}$ . Prove que se ${A}$ e ${B}$ são independentes então pelo menos um desses eventos deve ser ${\emptyset}$ ou ${\Omega}$ .