[MCTB019-17] § 7 — Princípios de contagem: bijeções e cardinalidade

Publicado em por

Uma característica importante dos números naturais é que eles respondem a pergunta quantos elementos tem esse conjunto? Ou seja, os naturais constituem o modelo matemático que torna possível o processo de contagem.

Contagem é o processo de criar uma bijeção entre um conjunto que queremos contar e algum conjunto cujo tamanho já sabemos. O tamanho de um conjunto é chamado de cardinalidade. Geralmente, não fornecemos uma bijeção explícita para calcular o tamanho de um conjunto, mas sim nos baseamos em princípios de contagem derivados dos processos de construção de conjuntos. O ramo da matemática que estuda conjuntos construídos pela combinação de outros conjuntos é chamado de Combinatória e a subárea que estuda os métodos de contagem é chamada de Combinatória Enumerativa.

Cardinalidade é um conceito da Teoria dos Conjuntos que estende para qualquer conjunto a noção quantidade de elementos de um conjunto, a qual é intuitivamente clara no caso de conjuntos finitos: a cardinalidade de um conjunto finito é o número (natural) de elementos no conjunto. Os números cardinais transfinitos descrevem os tamanhos de conjuntos infinitos. Na verdade, a ideia de cardinalidade torna-se bastante sutil quando os conjuntos são infinitos. Há uma sequência transfinita de números cardinais:

\displaystyle \displaystyle 0,1,2,3, \ldots, n, \ldots; \aleph_{0}, \aleph_{1}, \aleph_{2}, \ldots, \aleph_{\omega} , \aleph_{\omega+1} , \ldots, \aleph_{\omega^2} , \ldots, \aleph_{\omega^\omega} , \ldots, \aleph_{\alpha} , \ldots.

Os índices dos números alef ({\aleph}) são números ordinais.

7.1. Bijeções

Para contar os elementos de um conjunto é usamos a noção de correspondência biunívoca, ou bijeção, ou função bijetiva. Dois conjuntos têm a mesma cardinalidade se, e somente se, há uma correspondência um-para-um (bijeção) entre os elementos dos dois conjuntos.

Definição 21 Uma função {f : X\rightarrow Y} é injetiva quando {\forall x, x'\in X\,(x\neq x' \Rightarrow f(x) \neq f(x'))}.

Uma função {f : X\rightarrow Y} é sobrejetiva quando {\forall y\in Y \, \exists x\in X \, (f(x)=y)}.

Uma função {f : X\rightarrow Y} é bijetiva quando for injetiva e sobrejetiva, isto é, quando {\forall y\in Y \, \exists! x\in X \, (f(x)=y)}.

Definição 22 A cardinalidade de {A} é denotada por {|A|}. Dois conjuntos têm a mesma cardinalidade, {|A|=|B|} se, e somente se, existe uma bijeção {f:A\rightarrow B}.

Escrevemos {|A|\leq |B|} para abreviar que existe {f : A\rightarrow B} injetiva.

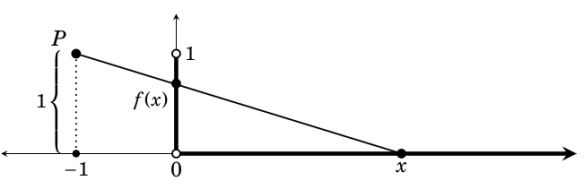
Exercício 30 Verifique que {f:{\mathbb R}^+ \rightarrow (0,1)}, dada por {f(x) = \frac x{x+1}} é bijetiva. A função {f} tem a seguinte interpretação gráfica

bijecao

Para cada {x\in (0,+\infty)} o valor {f(x)} é dado pela intersecção da reta que passa por {x} e por {P=(-1,1)} com o eixo {y}. Usando semelhança de triângulos temos

\displaystyle \frac{1}{x+1}=\frac{f(x)}{x}

donde tiramos a expressão para {f(x)}.

Exercício 31 Verifique que {g:{\mathbb R} \rightarrow {\mathbb R}^+}, dada por {g(x) = 2^x} é bijetiva.

Exercício 32 Prove que se {g:A\rightarrow B} e {f: B\rightarrow C} são bijeções então a função composta {f\circ g : A \rightarrow C} é bijeção.

Alguns exemplos importantes

  1. {|{\mathbb N}|=|{\mathbb Z}|};

    2. Para mostrar que {|{\mathbb N}|=|{\mathbb Z}|} definimos a função {f : {\mathbb Z} \rightarrow {\mathbb N}} dada por

    \displaystyle f(z) = \Bigg\{ \begin{array}{ll} 2z, & \text{ se } z\geq0\\ 2(-z) - 1, & \text{ se } z< 0. \end{array}

    Dado {n\in {\mathbb N}}, se {n} é par então {n=2z} para algum {z\in {\mathbb N}}, portanto {f(z)=n}; senão {n} é ímpar, {n=2z-1} para algum {z\in{\mathbb Z}^+}, portanto {f(-z)=2(-(-z))-1=n}. Assim {f} é sobrejetora. Agora, se {f(z_1)=f(z_2)} então {2z_1=2z_2} ou {2(-z_1)+1=2(-z_2)-1} e em ambos os casos {z_1=z_2}. Portanto a função é bijetora. \Box

  2. {|{\mathbb N}|=|{\mathbb Q}|};

    3. Claramente há uma função injetiva {f : {\mathbb N} \rightarrow {\mathbb Q}} pois {{\mathbb N} \subset {\mathbb Q}}, logo {|{\mathbb N}|\leq |{\mathbb Q}|}. Para mostrar que {|{\mathbb Q}|\leq |{\mathbb N}|} consideremos os racionais não-nulo dados pelas frações da forma

    \displaystyle \frac pq, ~p\in {\mathbb Z} ~\mathrm{e}~ q\in {\mathbb N}, ~\mathrm{mdc}(p,q)=1

    agora, definimos {g : {\mathbb Q}\rightarrow {\mathbb N}} por {g(0)=0} e

    \displaystyle g\left( \frac pq \right) = \Big\{ \begin{array}{ll} 2^p 3^q, & \text{ se }p>0\\ 5^p 3^q, & \text{ se }p<0 \end{array}

    que é injetiva (verifique). É possível exibir um bijeção entre {{\mathbb Q}} e {{\mathbb N}} mas isso também é bastante trabalhoso.\Box

  3. {|{\mathbb R}|=|(0,1)|};

    4. Dos exercícios 30 e 31 temos as bijeções {f:{\mathbb R}^+ \rightarrow (0,1)}, dada por {f(x) = \frac x{x+1}}, e {g:{\mathbb R} \rightarrow {\mathbb R}^+}, dada por {g(x) = 2^x}, que estabelecem que {|{\mathbb R}| = |(0,1)|} pois {f\circ g : {\mathbb R}\rightarrow (0,1)} também é bijeção. \Box

  4. {|{\mathbb N}|<|{\mathbb R}|};

    5. Neste exemplo temos a famosa demonstração de Cantor por diagonalização. Como {{\mathbb N}\subset {\mathbb R}}, temos {|{\mathbb N}|\leq |{\mathbb R}|} logo precisamos mostrar que {|{\mathbb N}|\neq |{\mathbb R}|}. Para tal, mostraremos que {|{\mathbb N}|\neq |(0,1)|}. Suponha que exista {f : {\mathbb N} \rightarrow (0,1)} bijetiva. Se existe tal {f} então podemos enumerar (todos) os elementos do intervalo

    \displaystyle \begin{array}{rcl} f(0) &= 0{,}{d_{0,0}}d_{0,1}d_{0,2}d_{0,3}d_{0,4}\dots d_{0,n}\dots \\ f(1) &= 0{,}d_{1,0}{d_{1,1}}d_{1,2}d_{1,3}d_{1,4}\dots d_{1,n}\dots \\ f(2) &= 0{,}d_{2,0}d_{2,1}{d_{2,2}}d_{2,3}d_{2,4}\dots d_{2,n}\dots \\ \vdots& \\ f(n) &= 0{,}d_{n,0}d_{n,1}d_{n,2}d_{n,3}d_{n,4}\dots {d_{n,n}}\dots\\ \vdots& \end{array}

    com {d_{i,j}\in\{0,1,2,3,4,5,6,7,8,9\}}. Consideremos o número real

    \displaystyle \alpha=0{,}d_0d_1d_2d_3\dots d_n\dots \text{ com } d_i \in \{0,1,2,3,4,5,6,7,8,9\} \setminus \{0,9,d_{i,i}\} ~(\forall i\in{\mathbb N}).

    Esse número {\alpha} pertence ao intervalo {(0,1)} pois {d_i\neq 0}, logo {\alpha} é diferente de {0=0{,}00000\dots}, e {d_i\neq 9} logo {\alpha} é diferente de {1=0{,}9999\dots}. Ademais, {\alpha \neq f(i)} pois {d_i\neq d_{i,i}} para todo {n\in{\mathbb N}}, uma contradição. Portanto, não existe {f : {\mathbb N} \rightarrow (0,1)} bijetiva, tampouco {f : {\mathbb N} \rightarrow {\mathbb R}} bijetiva. \Box

  5. {|{\mathbb R}^2|=|{\mathbb R}|};

    6. Aqui é suficiente basta mostrarmos que {|(0,1)\times (0,1)| \leq |(0,1)|} pois, claramente, temos { |(0,1)| \leq |(0,1)\times (0,1)|} pela injetiva {f(x) = (x,1)} para todo {x}.

    Um ponto no quadrado {(0,1)\times (0,1)} é da forma {(x,y)} com {x=0{,}a_1a_2a_3\dots} e {y=0{,}b_1b_2b_3\dots} e uma função injetiva sobre {(0,1)} é dada quando mapeamos tal ponto em {0{,}a_1b_1a_2b_2a_3b_3\dots} de {(0,1)}.\Box

  6. {| 2^{\mathbb N}|=|{\mathbb R}|}.Que {|2^{\mathbb N}| \leq |(0,1)|}: um subconjunto {B \subseteq {\mathbb N}} pode ser representado por uma sequência binária infinita {b_0b_1b_2\dots} em que {b_i=1 \Leftrightarrow i\in B}, para todo {i\in{\mathbb N}}. Essa sequência é mapeada na representação binária {0{,}b_0b_1b_2\dots} de um número real do intervalo {(0,1)}; tal função é injetora (verifique).

    Que {|(0,1)| \leq |2^{\mathbb N}| }: defina {f(0{.}d_1d_2d_3,\dots) = \{10d_1,10^2d_2, 10^3d_3,\dots\}} e verifique que {f} é injetiva. \Box

Sob a hipótese do contínuo {\aleph_1=|{\mathbb R}|}.

7.2. Conjuntos finitos

Definimos {I_n = \{1,2,\dots,n\}} para todo natural {n\geq 1}.

Definição 23 A cardinalidade do vazio é {0}, {|\emptyset|=0} . Se {A\neq \emptyset} então {|A|=n} se existe uma bijeção {f : I_n \rightarrow A}.

Definição 24 {A} é finito se {|A|=n} para algum {n \in{\mathbb N}}.

Uma tal bijeção {f:I_n\rightarrow A} é chamada de enumeração ou contagem dos elementos de {A}. Desse modo, {A=\{f(1),f(2),\dots,f(n)\}} e dizemos que {A} tem {n} elementos.

Exercício 33 Se {A\neq \emptyset} é conjunto e {f : I_n \rightarrow A} e {g : I_m \rightarrow A} são bijeções então {m=n}.

Note que a relação de ordem entre cardinais, definição 22, no caso finito concorda com a representação conjuntista de número natural que apresentamos na ocasião dos Axiomas de ZFC: {1=\{\emptyset\}}, {2=\{0,1\}, \dots, n=\{0,1,\dots,n-1\}} {\dots} Assim {3\leq 4} pois existe {f : \{0,1,2\} \rightarrow \{0,1,2,3\}} injetiva, a saber {f(n)=n}.

Teorema 38 (princípio aditivo) Se {A} e {B} são conjuntos finitos e disjuntos, então {|A\cup B|=|A|+|B|}.

Demonstração: Sejam {A} e {B} conjuntos disjuntos com cardinalidade {n} e {m}, respectivamente. Se pelo menos um deles for vazio então o teorema vale como pode ser verificado facilmente.

Vamos supor {m,n >0} e vamos mostrar uma bijeção {h : I_{n+m}\rightarrow A\cup B}.

Se { f : I_n \rightarrow A} e { g : I_m \rightarrow B} são bijeções então definimos {h} por

\displaystyle h(x) = \Bigg\{ {\begin{array}{ll} f(x) &\text{ se }1\leq x\leq n\\ g(x-n) &\text{ se }n+1\leq x\leq n+m. \end{array}}

{h} é sobrejetora: se {y\in A\cup B}, então {y\in A} ou {y\in B}, mas não em ambos já que são disjuntos. Se {y\in A} então {f(x)=y} para algum {x\in \{1\dots,n\}}, portanto {h(x)=y}. Se {y\in B} então {g(x)=y} para algum {x\in \{1\dots,m\}}, portanto, {h(x+n)=g(x)}. Ainda, {h} é injetora: como {A} e {B} são disjuntos, se {h(x)=h(y)} então {f(x)=f(y)} ou {g(x)=g(y)}, em ambos os casos {x=y}. \Box

Exercício 34 Prove usando indução em {n} que se {A_1,\dots,A_n} são conjuntos dois-a-dois disjuntos então

\displaystyle \left| A_1 \cup A_2 \cup \cdots \cup A_n \right| = |A_1| + |A_2| + \cdots + |A_n|.

Teorema 39 (princípio multiplicativo) Se {A} e {B} são conjuntos finitos não vazios, então {|A\times B| = |A|\cdot|B|}.

Demonstração: Seja {n=|A|} e {A=\{f(1),f(2),\dots,f(n)\}} para alguma enumeração {f} de {A}. Definimos os conjuntos dois-a-dois disjuntos

\displaystyle E_i=\{(f(i),b)\in A\times B : b\in B\}

de modo que {|E_i|=|B|}, para todo {i}, pela bijeção {g_i \big( (f(i),b) \big) = b}.

Assim, {\{E_1,\dots,E_n\}} é uma partição de {A\times B} (verifique) e

\displaystyle |A\times B|= \left|\bigcup_{i=1}^n E_i\right| = \sum_{i=1}^n |B|=|A||B| \ \ \ \ \ (38)

onde a segunda igualdade segue do exercício 34. \Box

Exercício 35 Prove o teorema acima exibindo uma bijeção entre {I_{|A||B|}} e {A\times B}.

Exercício 36 { |\{0,1\}^n|= 2^n} (prove usando indução em {n} uma generalização do princípio multiplicativo e use-a para concluir a igualdade proposta).

Teorema 40 Todo conjunto {A} de cardinalidade {n\in{\mathbb N}} tem {2^n} subconjuntos distintos, isto é,

\displaystyle |2^A|=2^{|A|}.

Demonstração: Seja {A} um conjunto de cardinalidade {n}. Se {n=0} então {A=\emptyset} é o único subconjunto dele mesmo e {2^0=1}.

Se {n\geq 1} então existe uma bijeção {f : I_n\rightarrow A}. Como {A=\{f(1),f(2),f(3),\dots,f(n)\}}, cada subconjunto {B\subset A} corresponde a uma, e só uma, sequência {\mathbf{b}(B) = (b_1,b_2,\dots,b_n)\in \{0,1\}^n} dada por

\displaystyle b_i=1 \Leftrightarrow f(i) \in B

para cada {i\in \{1,2,\dots,n\}}, ou seja

\displaystyle \begin{array}{rcl} \mathbf{b} : 2^A & \rightarrow & \{0,1\}^n \\ B & \mapsto & \mathbf{b}(B) \end{array}

assim definida é bijetiva (verifique), de modo que {|2^A| = |\{0,1\}^n|}, portanto { |2^A|= 2^n}. \Box

Teorema 44 (Princípio da Casa dos Pombos) Sejam {E} e {F} conjuntos finitos não vazios. Se existe função {f : E \rightarrow F} injetiva então {|E| \leq |F|}.

Antes de demonstrar esse resultado definimos a imagem inversa de {y\in F} pela função {f} como o conjunto

\displaystyle f^{-1}(y) = \{ x\in E : f(x)=y\}

e notemos que se {f} for sobrejetiva então {f^{-1}(y) \neq \emptyset} para todo {y\in F},e se {f} for injetiva então {|f^{-1}(y)|\leq 1} para todo {y\in F}.

Demonstração: Sejam {E} e {F\neq\emptyset} conjuntos finitos. Suponha que que {f : E \rightarrow F} seja uma função injetiva.

Se {F} é finito, então existe {h: I_m \rightarrow F} para algum {m\in\ N}, de modo que

\displaystyle F=\{h(1), h(2), \dots,h(m)\}.

Se {f : E \rightarrow F} é função então {E} é a união

\displaystyle E= f^{-1}(\,h(1)\,) \cup f^{-1}(\,h(2)\,) \cup \cdots \cup f^{-1}(\,h(m)\,)

de conjuntos disjuntos dois-a-dois. Ademais, se {f} injetiva então {|f^{-1}(\,h(i)\,) | \leq 1} para todo {i\in\{1,2,\dots,m\}}. Pelo princípio aditivo

\displaystyle |E|= |f^{-1}(\,h(1)\,)| + |f^{-1}(\,h(2)\,)| + \cdots + |f^{-1}(\,h(m)\,)|

Pela injetividade

\displaystyle |f^{-1}(\,h(1)\,)| + |f^{-1}(\,h(2)\,)| + \cdots + |f^{-1}(\,h(m)\,)| \leq m

portanto {|E| \leq |F|}. \Box

Corolário 45 Sejam {E} e {F} conjuntos finitos não vazios. Se {|F| < |E|} então para toda {f : E \rightarrow F} existe {y\in F} tal que

\displaystyle |f^{-1}(y)| \geq \frac{|E|}{|F|}.

Demonstração: Seguindo a demonstração do teorema, se não existe tal {y} então

\displaystyle |E|= |f^{-1}(\,h(1)\,)| + |f^{-1}(\,h(2)\,)| + \cdots + |f^{-1}(\,h(m)\,)| < |F| \frac{|E|}{|F|}

que é uma contradição. \Box

Exemplo: Dado {n\in{\mathbb N}}, existem números inteiros positivos {a} e {b}, com um {a\neq b}, tal que {n^a-n^b} é divisível por {10}. Considere os seguintes {11} números

\displaystyle n^1 \qquad n^2 \qquad n^3 \qquad n^4 \qquad n^5 \qquad n^6 \qquad n^7 \qquad n^8 \qquad n^9 \qquad n^{10} \qquad n^{11}

como há 10 possibilidades para o algarismo da unidade, a saber {\{0,1,2,\dots,9\}}, dois desses números, digamos {n^a} e {n^b} com {a\neq b}, termina com o mesmo algarismo de modo que {n^a -n^b} é divisível por 10.

Exercício 39 Se cinco pontos são distribuídos num quadrada de lado 1 então há dois deles cuja distância é no máximo {\sqrt 2/2}.

Exemplo: Em qualquer escolha de mais que {n} números do conjunto {\{1,2,\dots,2n\}} um dos escolhidos será múltiplo de um outro escolhido. Se {r\in \{1,2,\dots,2n\}} então, pelo teorema fundamental da aritmética, esse número pode ser escrito de forma única como {r=2^a t} com {a,t} naturais e {t} ímpar. Se {t} é ímpar, então {t\in \{1,3,5,7,\dots,2n-1\}}. Então, em mais que {n} números dois deles terão o mesmo divisor ímpar, digamos {r=2^a t} e {s=r=2^b t}. O maior deles é múltiplo do menor.

Exercício 40 Em qualquer escolha de mais que {n} números do conjunto {\{1,2,\dots,2n\}} haverão dois deles primos entre si.

7.3. Conjuntos enumeráveis

O conjunto {A} é dito enumerável se é finito ou se tem a mesma cardinalidade de {{\mathbb N}}, isto é {|A|=|{\mathbb N}|} de modo que {A=\{f(1),f(2),\dots\}}. {{\mathbb N}}, {{\mathbb Z}} e {{\mathbb Q}} são enumeráveis. {{\mathbb R}} não é enumerável.

O conjunto dos naturais não é finito. De fato, se houvesse uma bijeção {f : I_n \rightarrow {\mathbb N}} então tomaríamos o número natural {m=f(1)+f(2)+\cdots+f(n)} de modo que {m} pertenceria à imagem de {f} contradizendo que {m > f(i)} para todo {i\in \{1 ,\dots, n\}}.

7.4. Conjuntos infinitos

Definição 25 {A} é infinito se, e só se, não é finito.

No caso de conjuntos infinitos não se pode falar em quantidade de elementos e, além disso, dizer simplesmente que são infinitos elementos não diz muita coisa desde que Cantor nos mostrou a possibilidade de vários “tamanhos” de infinito, como veremos a seguir.

Definição 26 {\aleph_0 =|{\mathbb N}|} é o menor cardinal infinito.

Teorema 41 (Teorema de Cantor) Para todo conjunto {A}, {|A| < |2^A|}.

Demonstração: Se {A} é finito então {|A|< 2^{|A|}}. Seja {A} um conjunto infinito e vamos mostrar que {|A| \leq | 2^A|} e que {|A| \neq | 2^A|}. A função

\displaystyle \begin{array}{rcl} f : A &\rightarrow& 2^A \\ a &\rightarrow & \{a\} \end{array}

é injetiva, portanto {|A| \leq | 2^A|}.

Para mostrar que {|A| \neq |2^A|} provaremos (por contradição) que não há sobrejeção { g : A \rightarrow 2^A}.

Suponhamos que { g : A \rightarrow 2^A} é sobrejetiva. Definimos

\displaystyle B = \{a\in A : a\notin g(a)\}.

{B\subset A} e {g} sobrejetiva implica que {B=g(b)} para algum {b}.

Se {b\in B} então {b\not\in g(b)=B}, pela definição do conjunto {B}. Também, se {b\not\in B} então {b\in g(b)=B}, ou seja, {b\not\in B \Leftrightarrow b\in B}, uma contradição. \Box

Em particular, temos

\displaystyle |{\mathbb N}| < |2^{{\mathbb N}}| < |2^{2^{{\mathbb N}}}| < |2^{2^{2^{{\mathbb N}}}} | < \cdots

A hipótese do contínuo: Por quase um século após a descoberta de Cantor de que há diferentes infinitos muitos matemáticos atacaram o problema de descobrir se existe um conjunto {A} tal que {|{\mathbb N}| < |A| < |2^{{\mathbb N}}|}. Suspeitava-se que tal conjunto não existiria e a proposição que não existe tal {A} é conhecida como hipótese do contínuo. Gödel, nos anos 1930, provou que a negação da hipótese do contínuo não pode ser provada a partir dos axiomas ZFC. Em 1964, Paul Cohen descobriu que nenhuma prova pode deduzir a hipótese do contínuo a partir dos axiomas de ZFC. Tomados em conjunto, os resultados de Gödel e Cohen significa que dos axiomas padrão da Teoria dos Conjuntos não se pode decidir se a hipótese do contínuo é verdadeira ou falsa; nenhum conflito lógico surge a partir da afirmação ou negação da hipótese do contínuo. Dizemos que a hipótese do contínuo é independente de ZFC. Assumindo a hipótese do contínuo

\displaystyle \begin{array}{rcl} \aleph_0 &=& |{\mathbb N}| \\ \aleph_{\alpha+1} &=& |2^{\aleph_{\alpha}}| \\ \end{array}

O seguinte resultado é bastante famoso, ele é altamente não trivial no caso de conjuntos infinitos. A utilidade deste resultado vem do fato que, em geral, estabelecer uma bijeção que comprove {|A| = |B|} pode ser muito difícil enquanto que estabelecer funções injetivas que comprovem {|A| \leq |B|} e {|B| \leq |A|} é mais fácil.

Teorema 42 (Teorema de Cantor–Bernstein–Schröder) Se {|A| \leq |B|} e {|B| \leq |A|} então {|A| = |B|}.

Uma demonstração será dada adiante.

Uma dúvida que pode surgir nesse momento é saber se vale a lei de tricotomia para cardinalidades, ou seja, para quaisquer {A} e {B}, ou {|A|<|B|}, ou {|A|=|B|}, ou {|B|<|A|}. De fato, vale tal lei se assumirmos que vale o axioma da escolha. Nesse caso, vale que para qualquer conjunto {A}

  1. se {|A| < |{\mathbb N}|} então {A} é finito e enumerável;
  2. se {|A| = |{\mathbb N}|} então {A} é infinito e enumerável;
  3. se {|{\mathbb N}| < |A| } então {A} é infinito e não enumerável.

Demonstração do Teorema de Cantor–Bernstein–Schröder (opcional): Antes de demonstrar o teorema vamos adotar a seguinte convenção notacional: {\overline{A}^X = X\setminus A}.

Demonstração: Sejam {A} e {B} conjuntos tais que {|A| \leq |B|} e {|B| \leq |A|} e vamos mostrar que {|A| = |B|}. Sejam {f : A \rightarrow B} e {g : B \rightarrow A} funções injetivas, que existem por hipótese. Vamos mostrar que existe uma bijeção {h : A \rightarrow B}. Definimos, para todo {X\subset A}

\displaystyle F(X) = A \setminus g( B \setminus f(X) ) = A \setminus g \left( \overline{f(X)}^{B} \right) = \overline{ g \left( \overline{f(X)}^{B} \right)}^A

onde {f(X)} é o subconjunto de {B} formado pela imagem dos elementos de {X}. Vamos mostrar que existe {A_0 \subset A} tal que {F(A_0) = A_0}. Primeiro, notemos que par uma sequência qualquer {(A_i : i\geq 1)} de subconjuntos de {A} temos

\displaystyle \begin{array}{rcl} F\left( \bigcap_{i\geq 1} A_i \right) &= \overline{g \left( \overline{ f(\bigcap_{i\geq 1} A_i)}^{B}\right)}^A & \text{ por defini\c{c}\~ao}\\ &= \overline{g \left( \overline{ \bigcap_{i\geq 1} f(A_i)}^{B}\right)}^A & \text{ pois f \'e injetiva}\\ &= \overline{g \left( \bigcup_{i\geq1}\overline{f(A_i)}^{B} \right)}^A& \text{ por De Morgan}\\ &= \overline{ \bigcup_{i\geq1} g \left( \overline{f(A_i)}^{B} \right)}^A& \text{ pois g \'e injetiva}\\ &= \bigcap_{i\geq 1} \overline{ g \left( \overline{f(A_i)}^{B} \right)}^A& \text{ por De Morgan}\\ &= \bigcap_{i\geq 1} F(A_i) &\text{ por defini\c c\~ao de F}. \end{array}

Tomemos

\displaystyle A_0 = A \cap F(A) \cap F^2(A) \cap F^3(A)\cap \cdots

onde {F^n (A) = F( F^{n-1}(A))} donde temos

\displaystyle F(A_0) = F\Big( A \cap F(A) \cap F^2(A) \cap F^3(A)\cap \cdots \Big) = F(A) \cap F(F(A)) \cap F(F^2(A)) \cap F(F^3(A) )\cap \cdots

logo {F(A_0) = F(A) \cap F^2(A) \cap F^3(A) \cap F^4(A) \cap \cdots = A_0 } pois {A \supset F(A) \supset F^2(A) \supset \cdots}. Desse modo { h : A \rightarrow B} dada por

\displaystyle h(x)= \begin{array}{ll}\Bigg\{ f(x), & \text{ se } x\in A_0 \\ g^{-1}(x), & \text{ caso contr\'ario, isto \'e } x\in g\Big(\overline{f(A_0)}^B\Big) \end{array} \ \ \ \ \ (39)

é uma bijeção. Que é sobrejetiva: seja {y\in B}. Se {y\in f(A_0)}, então {y=f(x)} para {x\in A_0}, portanto {y=h(x)}; senão, {y\not\in f(A_0)}, ou seja {y\in \overline{f(A_0)}^B}, logo {g(y) \not\in A_0} logo {h(g(y))= g^{-1}(g(y))=y}, portanto {h} é sobrejetora. Que é injetiva: sejam {x,y\in A} com {x\neq y}. A demonstração segue em três casos; {(i)} se {x,y\in A_0} então {h(x) = f(x) \neq f(y) =h(y)}; {(ii)} se {x\in A_0}, então {h(x)= f(x) \in f(A_0)}, e se {y\not\in A_0}, ou seja {y\in g\Big(\overline{f(A_0)}^B\Big)}, então {h(y) = g^{-1}(y) \in g^{-1}\Big( g\Big(\overline{f(A_0)}^B\Big)\Big) = \overline{f(A_0)}^B}, portanto {h(x) \neq h(y)}; {(iii)} se {x,y\not\in A_0} então {h(x) = g^{-1}(x) \neq g^{-1}(y) = h(y)}. Em todos os casos {h(x)\neq h(y)}, logo {h} é injetora. \Box

 

4 respostas em “[MCTB019-17] § 7 — Princípios de contagem: bijeções e cardinalidade”

  1. Professor,

    Primeiramente, obrigada pelo post, foi muito útil. Segundamente, gostaria de apontar que, no item 7.5, está escrito:

    1. se |A| |A|, então A é infinito e não enumerável.

    Isso está certo, ou é o sinal de > que apareceu trocado?

    Comentar ↓

  2. Na definição 21, quando é definido o que é uma função bijetiva está escrito:
    “Uma função … é bijetiva quando for injetiva e bijetiva..”, acredito que onde é dito “injetiva e bijetiva” deveria ser “injetiva e sobrejetiva”.

    Comentar ↓

Deixe um comentário