[MCTB019-17] § 9 — Princípios de contagem: combinatória

Uma interpretação para o princípio aditivo é: suponha que o evento ${E}$ pode ocorrer ${n}$ maneiras e o evento ${F}$ de ${m}$ maneiras distintas das outras ${n}$ . Então, o número de maneiras de ocorrer o evento “ ${E}$ \underline{ou} ${F}$ ” é ${n+m}$ . No caso geral, se ${A_1,\dots,A_n}$ são conjuntos dois-a-dois disjuntos então

$\displaystyle \left| A_1 \cup A_2 \cup \cdots \cup A_n \right| = |A_1| + |A_2| + \cdots + |A_n|.$

Por exemplo, há quantas possibilidades de escolher um inteiro entre ${1}$ e ${16}$ que é múltiplo de ${3}$ ou de ${7}$ ? Devemos determinar a cardinalidade do conjunto de inteiros entre ${1}$ e ${16}$ que são múltiplos de ${3}$ ou múltiplos de ${7}$ , tais conjuntos são disjuntos pois ${\mathrm{mmc}(3,7)=21}$ . Os múltiplos de ${3}$ são cinco, os múltiplos de ${7}$ são dois, portanto, os múltiplos de ambos são ${5+2=7}$ . O evento múltiplo de ${3}$ ou múltiplo de ${7}$ ocorre de ${7}$ modos distintos.

Teorema 43 (Princípio de Inclusão–Exclusão) Se ${E}$ e ${F}$ são conjuntos finitos (não necessariamente disjuntos) então

$\displaystyle |E\cup F|= |E|+|F| -|E\cap F|. \ \ \ \ \ (40)$

Demonstração:
Sejam ${E}$ e ${F}$ conjuntos finitos. Podemos escrever ${E\cup F}$ como a seguinte união de subconjuntos disjuntos (verifique)

$\displaystyle E\cup F= E \cup (F\setminus E)$

portanto, pelo princípio aditivo

$\displaystyle |E\cup F|= |E| + |F\setminus E| . \ \ \ \ \ (41)$

Também podemos escrever ${F}$ como uma união disjunta (verifique)

$\displaystyle F = ( F\setminus E )\cup (E\cap F)$

portanto ${|F| = |F\setminus E| + |E\cap F|}$ donde deduzimos

$\displaystyle |F\setminus E| = |F| - |E\cap F|. \ \ \ \ \ (42)$

Substituindo (42) em (41) ${ |E\cup F| = |E| + |F| - |E\cap F| . }$ $\Box$

Por exemplo, o número de possíveis resultados que são múltiplo de 2 ou de 3 no lançamento de uma dado é dado por: os múltiplos de 2 definem o subconjunto ${E=\{2,4,6\}}$ , os múltiplos de 3 definem o subconjunto ${F=\{3,6\}}$ , portanto,

$\displaystyle |E \cup F| = |E| + |F| -|E\cap F| = 4. \ \ \ \ \ (44)$

Exercício 37 Prove que se ${A}$ , ${B}$ e ${C}$ são conjuntos finitos então

$\displaystyle |A\cup B\cup C|= |A|+|B|+|C| - |A\cap B|-|B\cap C|-|A\cap C| + |A\cap B \cap C|. \ \ \ \ \ (45)$

Exemplo: Em uma academia de arte, há 43 estudantes que tomam aula de cerâmica, 57 estudantes que fazem pintura e 29 estudantes que tomam aula de escultura. Há 10 alunos em cerâmica e pintura, 5 em pintura e escultura, 5 em cerâmica e escultura e 2 tendo todos os três cursos. Quantos alunos alunos estão fazendo pelo menos um curso na academia de arte? Vamos indicar por ${C}$ , ${P}$ e ${E}$ os conjuntos de alunos que fazem cerâmica, pintura e escultura, respectivamente. Queremos calcular ${|C\cup P\cup E|}$ . Aplicamos inclusão–exclusão: ${|C\cup P\cup E|= |C|+|P|+|E| - |C\cap P|-|P\cap E|-|C\cap E| + |C\cap P \cap E| =111}$ .

Exercício 38 De quantas maneiras podemos escolher um número em ${\{1,2,\dots,100\}}$ que não é divisível por ${2}$ , ${3}$ ou ${5}$ ?

Uma interpretação para o princípio multiplicativo é: se um evento pode ser descrito em duas etapas de modo que há ${n}$ desfechos possíveis para a ${1^{\tiny\mathrm{a}}}$ etapa e há ${m}$ desfechos possíveis para a ${2^{\tiny\mathrm{a}}}$ etapa, então o número de possíveis desfechos para o evento é ${n \cdot m}$ .

De um modo geral, se ${E_1}$ , … ${E_r}$ representam ${r}$ etapas de evento composto, então o números de modos distintos de realizar o evento é

$\displaystyle \left| \prod_{i=1}^r E_i \right| = |E_1|\cdot|E_2|\cdots|E_r| \ \ \ \ \ (46)$

que pode ser demonstrado usando princípio da indução.

Exercício 41 Uma placa de carro é uma sequência de 3 letras seguidas por 4 dígitos. Qual é a quantidade de placas distintas que podemos obter?

Esboço de solução: ${E_i=\{A,B,\dots,Z\}}$ para ${i=1,2,3}$ .

${E_i=\{0,1,2,3,4,5,6,7,8,9\}}$ para ${i=4,5,6,7}$ .

${\left|\prod_{i=1}^8 E_i \right| = 26 \cdot 26 \cdot 26 \cdot 10 \cdot 10 \cdot 10 \cdot 10 = 26^3 10^4= 175.760.000}$ . $\Box$

Exemplo: Cada posição da memória (célula de memória) de um computador tem um endereço que é uma sequência binária. As arquiteturas com processadores 32-bits tem capacidade para endereçamento de ${2^{32}= 4.294.967.296}$ posições de memória, aproximadamente ${4}$ Gigabytes. As arquiteturas com processadores 64-bits tem capacidade para endereçamento de

$\displaystyle 2^{64}= 18.446.744.073.709.551.616$

posições de memória, aproximadamente ${16}$ Exabytes (16 milhões de Terabytes). Suponhamos que um dispositivo de ${1}$ Gigabyte ocupe um dispositivo de dimensões ${1\,\mathrm{mm} \times 1\,\mathrm{mm} \times 1\,\mathrm{mm} }$ . Para guardar ${16}$ Exabytes precisaríamos de uma quarto de dimensões ${2{,}5\,\mathrm{m}\times 2{,}5\,\mathrm{m}\times 2{,}5\,\mathrm{m}}$ .

A seguir destacamos alguns casos particulares do princípio multiplicativo. Essencialmente são dois tipos de listas: arranjos e combinações. Nos arranjos a ordem dos elementos importa e nas combinações a ordem não importa.

9.1. Arranjos

Quantas palavras (sequências) de 3 letras distintas do alfabeto latino podem ser formadas? Como o alfabeto tem 26 letras, pelo princípio multiplicativo são ${26\cdot 25\cdot 24}$ palavras.

Definição 27 Um arranjo simples de ${r\geq 1}$ elementos tomados de um conjunto ${A}$ de ${n\geq r}$ elementos é uma sequência ${(a_1,a_2,\dots,a_r)}$ de elementos não repetidos de ${A}$ . A quantidade de arranjos simples de ${r}$ elementos tomados de um conjunto de ${n}$ elementos ( ${r\leq n}$ ) é o número ${(n)_r}$ dado por

$\displaystyle (n)_r = n(n-1)(n-2) \cdots (n-r+1) \ \ \ \ \ (47)$

Quando é permitido repetição dizemos arranjo com repetição que é um caso particular do Princípio Multiplicativo com todos os conjuntos iguais. A quantidade de arranjos com repetição de ${r}$ elementos tomados de um conjunto de ${n}$ elementos é o número ${n^r}$ .

Por arranjo nos referimos a arranjo simples. Alguns textos usam a notação ${A(n,r)}$ para ${(n)_r}$ .

Exemplo: De quantas maneiras podemos escolher um inteiro entre ${000}$ e ${999}$ (inclusive e com 3 dígitos) com todos os dígitos distintos? O conjunto tem ${1.000}$ elementos e a quantidade deles sem dígitos repetidos é ${(10)_3= 10\cdot 9\cdot 8=720}$ .

Paradoxo do aniversário: Com que probabilidade ocorre que num grupo com 25 pessoas 2 ou mais pessoas façam aniversário no mesmo dia? O aniversário de 25 pessoas pode ocorrer de ${365^{25}}$ modos diferentes. O aniversário de 25 pessoas sem que nenhum deles coincida pode ocorrer de ${(365)_{25}}$ modos diferentes. Portanto, há ${365^{25}-(365)_{25}}$ possibilidades diferentes para o aniversário de 25 pessoas com pelo menos duas aniversariando no mesmo dia; a probabilidade desse evento é

$\displaystyle \frac{365^{25}-(365)_{25}}{365^{25}} = 1 - \frac{(365)_{25}}{365^{25}} > 0{,}56.$

Com 55 pessoas a probabilidade é maior que ${98\%}$ .

Exercício 42 Sejam ${A}$ e ${B}$ conjuntos finitos com ${|A|\leq |B|}$ . Há quantas funções injetivas de ${A}$ em ${B}$ ? E quantas são as funções de ${A}$ em ${B}$ ?

Permutação

Exemplo: De quantas maneiras diferentes 8 alunos podem se sentar numa sala com 8 cadeiras? O primeiro aluno tem 8 opções, o segundo tem 7, o terceiro tem 6, o quarto tem 5, o quinto tem 4, o sexto tem 3, o sétimo tem 2 e para o oitavo resta 1 opção. Logo há ${8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 40320}$ maneiras dos 8 alunos sentarem nas 8 cadeiras.

O caso de arranjo simples com ${r=n}$ é uma permutação. Quantas palavras com letras distintas podem ser formadas com as letras ${a}$ , ${b}$ e ${c}$ ? Pelo princípio multiplicativo são ${3\cdot 2\cdot 1=6}$ palavras.

Definição 28 Uma permutação de elementos de um conjuntos ${A}$ é uma sequência de elementos de ${A}$ . O número de permutações dos elementos de um conjunto de ${n\geq 0}$ elementos é

$\displaystyle \begin{array}{rcl} 0! &=& 1 \\ n! &=& n(n-1)! \text{ se }n\geq 1. \end{array}$

Exemplo: O número de permutações possíveis com as letras ${a}$ , ${b}$ , ${c}$ , ${d}$ e ${e}$ é ${5!=120}$ . O número de permutações possíveis com as letras ${a}$ , ${b}$ , ${c}$ , ${d}$ , ${e}$ e ${f}$ é ${6!6\cdot 5!=720}$ .

Exemplo: A quantidade de permutações que podem ser formadas com as letras da palavra ${livros}$ é ${6!=720}$ . A quantidade de permutações que podem ser formadas com as letras da palavra ${teclado}$ é ${7!=5.040}$ . A quantidade de permutações que podem ser formadas com as letras da palavra ${discreta}$ é ${8!=40.320}$ . A quantidade de permutações que podem ser formadas com as letras da palavra ${universal}$ é ${9!=362.880}$ . A quantidade de permutações que podem ser formadas com as letras da palavra ${pernambuco}$ é ${10!=3.628.800}$ . A quantidade de permutações que podem ser formadas com as letras da palavra ${seminublado}$ é ${11!=39.916.800}$ . A quantidade de permutações que podem ser formadas com as letras da palavra ${configuravel}$ é ${12!=479.001.600}$ .

Perceba que o fatorial cresce bastante rápido com ${n}$ :
${11!}$ é mais que a quantidade de segundos que passam em ${1}$ ano.
${12!}$ é mais que a quantidade de segundos que passam em ${12}$ anos.
${13!}$ é mais que a quantidade de segundos que passam em ${100}$ anos.

Notemos que

$\displaystyle (n)_r= \frac{n!}{(n-r)!}. \ \ \ \ \ (48)$

Permutação com repetição

Exercício 43 Qual é o número de permutações distintas com as letras da palavra ${{ana}}$ ?

Solução: [Solução] São ${3!}$ permutações de 3 símbolos, mas há permutações que dão origem a mesma sequência. As seis permutações de ana são:
ana, ana, aan, aan, naa, naa
em cada duas permutações a palavra é a mesma, só muda a ordem da letra repetida, portanto são

$\displaystyle \frac {3!}{ 2 !} = 3$

permutações distintas. $\Box$

Exercício 44 Qual é o número de permutações distintas com as letras da palavra ${{bala}}$ ?

Solução: da mesma maneira, das ${4!}$ permutações as ${2!}$ permutações que troca a ordem da letra igual e deixam as outras letras na mesma posição da sequência geram a mesma palavra, portanto são

$\displaystyle \frac {4!}{ 2 !} = 12$

permutações distintas. $\Box$

Exercício 45 Qual é o número de permutações distintas com as letras da palavra ${{banana}}$ ?

Solução: São ${6!}$ permutações de 6 símbolos. Mas agora há permutações que diferem apenas na ordem das letras ${a}$ ou das letras ${n}$ e dão origem a mesma sequência, por exemplo: são permutações diferentes que determinam a mesma sequência. As ${3!}$ permutações das letras ${a}$ são indistinguíveis, assim como as ${2!}$ da letras ${n}$ , portanto, há

$\displaystyle \frac {6!}{ 3! 2 !} = 60$

permutações distintas. $\Box$

Exercício 46 Um sinal é composto por nove bandeiras alinhadas. Quantos sinais diferentes é possível formar quando há disponíveis 4 bandeiras brancas, três bandeiras vermelhas e duas bandeiras azuis? Bandeiras da mesma cor são idênticas.

Esboço de solução: ${\frac {9!}{4!3!2!}=1.260}$ . $\Box$

Definição 29 No caso de permutações com repetição de objetos, se são ${n}$ objetos no total, com ${r}$ tipos de objetos distintos e ${k_i}$ objetos do tipo ${i}$ ( ${1\leq i\leq r}$ , ${n=k_1+\cdots+k_r}$ ) então temos ${n!}$ permutações donde descontamos as ${k_i!}$ permutações de objetos do mesmo tipo resultando

$\displaystyle \binom {n}{k_1,~k_2,\dots,~k_r} = \frac{n!}{k_1! k_2! \cdots k_r!} \ \ \ \ \ (49)$

Mão de bridge: Numa mão de Bridge as 52 cartas de um baralho embaralhado são divididas igualmente entre 4 jogadores. O número de modos distintos com que isso é feito pode ser calculado da seguinte forma: uma distribuição de cartas corresponde a uma sequência de 52 objetos, os 13 primeiros objetos da sequência são as cartas do primeiro jogador, os 13 seguintes do segundo jogador, os próximos 13 do terceiro e os 13 últimos objetos da sequência são as cartas do quarto jogador. Há ${52!}$ sequências distintas de cartas. Entretanto, dessas ${52!}$ temos que, para cada jogador, ${13!}$ permutações correspondem a mesma sequência de cartas em sua mão, portanto, são

$\displaystyle \binom{52}{13,13,13,13}=53.644.737.765.488.792.839.237.440.000$

modos distintos de distribuir as cartas, ou mãos diferentes de início de jogo.

Exercício 47 Se numa mão de Bridge as 52 cartas de um baralho são divididas igualmente e aleatoriamente entre 4 jogadores. Com que probabilidade cada jogador recebe um ás?

Solução: Os 4 ases podem ser distribuídos de ${4!}$ modos distintos entregando um para cada jogador. As 48 cartas restantes são distribuídas pelos jogadores de ${\binom{48}{12,12,12,12}}$ maneiras distintas. Pelo princípio multiplicativo são ${4!\binom{48}{12,12,12,12}}$ modos distintos de os jogadores receberem um ás cada. Portanto a probabilidade é

$\displaystyle \frac{4!\binom{48}{12,12,12,12}}{\binom{52}{13,13,13,13}}$

que vale aproximadamente ${0{,}0044}$ . $\Box$

Exercício 48 Quantos são as permutações das letras da palavra MATEMÁTICA?

Permutação circular

De quantos modos 5 crianças podem formar uma roda de ciranda? As rodas ${abcde}$ , ${eabcd}$ e ${deabc}$ , por exemplo, são iguais pois importa apenas a posição relativa entre as crianças. Assim cada roda pode ser girada de cinco maneiras e a resposta correta é ${5! / 5 = 4! = 24}$

Definição 30 O número de permutações circulares de ${n}$ objetos distintos, se consideramos equivalentes disposições que possam coincidir por rotação, é igual a

$\displaystyle (PC)_n = \frac{n !} n$

Aproximação de Stirling

Duas sequências de números ${a_n}$ e ${b_n}$ são assintoticamente iguais e escrevemos ${a_n \sim b_n}$ , se

$\displaystyle \lim_{n\rightarrow\infty} \frac{a_n}{b_n}=1.$

Frequentemente, é muito útil quanto trabalhamos com fatoriais a seguinte igualdade assintótica conhecida como fórmula de Stirling

$\displaystyle n! \sim n^n \mathrm{e}^{-n}\sqrt{2\pi n} \ \ \ \ \ (50)$

${n}$	${n!}$	stirling
${1}$	${1}$	${0.922137}$
${2}$	${2}$	${1.919004}$
${3}$	${6}$	${5.83621}$
${7}$	${5040}$	${4980.396}$
${10}$	${3628800}$	${3598696}$
${20}$	${2.432902e+18}$	${2.422787e+18}$
${50}$	${3.041409e+64}$	${3.036345e+64}$
${75}$	${2.480914e+109}$	${2.478159e+109}$
${100}$	${9.332622e+157}$	${9.324848e+157}$
${142}$	${2.695364e+245}$	${2.693783e+245}$

9.6. Combinações

Tomemos um arranjo de ${r}$ elementos escolhidos de um conjunto com ${n}$ elementos. A quantidade de arranjos que têm os mesmos ${r}$ elementos é ${r!}$ pois a única diferença entre eles é a ordem com que se apresentam os ${r}$ elementos. Por exemplo, se selecionamos sequencialmente e sem reposição ${3}$ cartas de um baralho então temos ${52\cdot 51\cdot 50}$ arranjos distintos, um dos quais é ${(\heartsuit K , \clubsuit 5 , \diamondsuit Q)}$ . Agora, se selecionamos três cartas de uma só vez as ${3!}$ permutações de ${(\heartsuit K , \clubsuit 5 , \diamondsuit Q)}$ correspondem a mesma seleção. A quantidade de seleções distintas é

$\displaystyle \frac{52\cdot 51\cdots 50}{3!}= \frac{52!}{49!3!}.$

Exercício 49 Seja ${A}$ um conjunto com ${n}$ elementos. Dado ${k}$ , ${0\leq k \leq n}$ , quantos subconjuntos de cardinalidade ${k}$ estão contidos em ${A}$ ?

Solução: Denote por ${ S(k,n)}$ a quantidade de subconjuntos de cardinalidade ${k}$ estão contidos em ${A}$ .

Um único subconjunto de tamanho ${k}$ determina ${k!}$ arranjos de ${k}$ elementos de ${A}$ . Subconjuntos distintos determinam arranjos distintos, portanto, ${ S(k,n)\cdot k! = (n)_k}$ , ou seja

$\displaystyle S(k,n)= \frac{(n)_k}{k!}$

Usando (48)

$\displaystyle S(k,n)= \frac{n!}{k!(n-k)!}$

$\Box$

Definição 31 Uma combinação de ${r}$ elementos escolhidos de um conjunto ${A}$ com ${n}$ elementos é simplesmente um subconjunto com ${r}$ elementos de ${A}$ . A quantidade de subconjuntos de ${A}$ com ${r}$ elementos, para ${0\leq r\leq n}$ , é o coeficiente binomial

$\displaystyle \binom nr = \frac{n!}{r!(n-r)!}.$

Convencionamos que ${\binom ab =0}$ se ${a<b}$ .

Exemplo (Mega-Sena): O jogo de apostas consiste em acertar 6 dezenas escolhidas dentre 60. O número de possíveis resultados distinto para a Mega-Sena é ${\binom{60}6 = 50.063.860}$ . Se uma aposta em seis números demorar 1 segundo para ser registrada, então registrar ${50.063.860}$ demoraria um ano e meio, aproximadamente. A probabilidade de acertar os seis números é

$\displaystyle \frac 1{\binom{60}6} = \frac 1{50.063.860} \approx 2\times 10^{-8}.$

A chance de morrer por raio no Brasil em 2010 era ${0{,}8\times 10^{-6}}$ (40 vezes maior. Esse número é uma média no sentido de que considera que todos têm a mesma chance de ser atingido, o que não é real).

Exemplo: Numa população com ${n}$ elementos, ${n_1}$ são azuis e ${n_2=n-n_1}$ são verdes. De quantas maneiras podemos escolher ${k}$ elementos com ${r}$ deles azuis? ${(0\leq r \leq \min\{n_1,k\})}$ O número de maneiras de escolher ${k-r}$ verdes é ${\binom {n_2}{k-r}}$ . O número de maneiras de escolher ${r}$ azuis é ${\binom {n_1}{r}}$ . Pelo Princípio Multiplicativo, o número de maneiras de escolher ${r}$ azuis e ${k-r}$ verdes é ${\binom {n_2}{k-r}\binom {n_1}{r}}$ .

Exercício 50 Prove que a seguinte identidade

$\displaystyle i\binom ni = n\binom{n-1}{i-1}. \ \ \ \ \ (51)$

Exercício 51 Três bolas são retiradas aleatoriamente de uma caixa com 6 bolas brancas e 5 bolas pretas. Com que probabilidade a escolha resulta em 1 branca e 2 pretas?

Solução: No total são 13 bolas das quais escolhemos 3. O número de possíveis resultados é ${\binom{13}3}$ . “6 bolas brancas e 5 bolas pretas” ocorre de ${\binom 61\binom 52}$ modos diferentes, pelo exercício anterior. Portanto a probabilidade é ${\frac {\binom 61\binom 52}{\binom{13}3}.}$ $\Box$

Combinação com repetição

Se escolhemos uma peça de dómino ao acaso, com que probabilidade obtemos ?

As peças de dominós são formadas por dois números tomados dos números de 0 a 6 podendo haver repetição. Os dominós com pares de números diferentes são ${\binom 72 = 21}$ , mais os ${7}$ pares repetidos resultam em ${28}$ peças de dominós, portanto, são ${28}$ combinações de 2 objetos tomados dentre 7 com repetição. Essa estratégia de contagem não é facilmente generalizável, o leitor pode tentar contar o número de peças de dominós de 5 pontas com 16 possíveis números diferentes, o resultado deverá ser ${15.504}$ .

A resposta para o caso geral: dentre ${n}$ objetos, queremos selecionar ${r}$ podendo haver repetição e sem considerar ordem. Isso pode ser feito de

$\displaystyle \binom{n+r-1}r \ \ \ \ \ (52)$

maneiras diferentes. No caso dos dominós, por exemplo, são ${7}$ números dos quais selecionamos ${2}$ , podendo repetir número

$\displaystyle \binom{7+2-1}2 = \binom 82 = \frac{8!}{6!2!}=28.$

Uma maneira de modelar combinação com repetição para deduzir equação (52) é escrever uma equação com uma indeterminada para cada um dos ${n}$ objetos, ${x_1,x_2,\dots,x_n}$ . A variável ${x_i}$ indica quantas vezes o ${i}$ -ésimo objeto será selecionado, portanto ${x_1+x_2+\cdots+x_n=r}$ . Assim, o número combinações com repetição é a quantidade de soluções inteiras de

$\displaystyle x_1+x_2+x_3+\cdots+x_n=r \text{ com } x_i \in \{0,1,2,\dots\} \text{ para todo } i. \ \ \ \ \ (53)$

Soluções inteiras de equações lineares

Vamos começar com um caso simples, estudaremos o número de soluções de

$\displaystyle x_1+x_2+x_3=6 \text{ com } x_i \in \{1,2,\dots\} \text{ para todo } i. \ \ \ \ \ (54)$

Escrevemos

$\displaystyle 1+1+1+1+1+1 = 6 \ \ \ \ \ (55)$

e uma solução da equação (54) corresponde a escolha de ${2}$ operadores ${\mathbf{+}}$ dentre os ${5}$ escritos na equação acima; por exemplo, se usamos ${\oplus}$ para representar as escolhas

$\displaystyle \underbrace{1+1}_{x_1} \oplus \underbrace{1+1+1}_{x_2} \oplus \underbrace{1}_{x_3} = 6 \ \ \ \ \ (56)$

corresponde a ${x_1=2}$ , ${x_2=3}$ e ${x_3=1}$ , e

$\displaystyle \underbrace{1+1}_{x_1} \oplus \underbrace{1+1}_{x_2} \oplus \underbrace{1+1}_{x_3} = 6 \ \ \ \ \ (57)$

corresponde a ${x_1=2}$ , ${x_2=2}$ e ${x_3=2}$ . Portanto essa equação tem ${\binom 52}$ soluções em ${{\mathbb Z}^+}$ .

Agora, estudaremos o número de soluções de

$\displaystyle x_1+x_2+x_3=6 \text{ com } x_i \in \{0,1,2,\dots\} \text{ para todo } i. \ \ \ \ \ (58)$

Notemos que uma solução ${(x_1,x_2,x_3)=(x,y,z)}$ inteira e positiva da equação ${ x_1+x_2+x_3=6+3}$ determina uma única solução inteira e não-negativa ${(x-1,y-1,z-1)}$ da equação ${x_1+x_2+x_3 =6}$ e vice-versa, ou seja, as equações

$\displaystyle \begin{array}{rcl} x_1+x_2+x_3 &= 6 + 3 & \text{ com } x_i \in \{1,2,3,\dots\} \text{ para todo } i. \\ x_1+x_2+x_3 &= 6 & \text{ com } x_i \in \{0,1,2,3,\dots\} \text{ para todo } i. \end{array}$

têm o mesmo número de soluções.

De volta ao problema que gerou essa discussão: o número de maneiras de selecionar ${r}$ objetos, podendo haver repetição, dentre ${n}$ objetos é igual ao número de soluções inteiras da equação (53), que é o mesmo número de soluções inteiras de

$\displaystyle x_1+x_2+x_3+\cdots+x_n= n + r \text{ com } x_i\in \{1,2,\dots\} \text{ para todo }i. \ \ \ \ \ (59)$

consideramos ${1+1+1+\cdots+1=n+r }$ e dos ${n+r-1}$ operadores ${+}$ escolhemos ${n-1}$ , ou seja, são ${ \binom{n+r-1}{n-1}}$ soluções inteiras. Finalmente, a equação (52) segue do seguinte exercício

Exercício 52 Verifique que vale

$\displaystyle \binom{n+r-1}r= \binom{n+r-1}{n-1} \ \ \ \ \ (60)$

para todo ${n}$ e todo ${r}$ para os quais os coeficientes binomiais estão definidos.

A quantidade de maneiras diferentes de selecionarmos ${r}$ elementos de um conjunto de ${n}$ elementos é,

	com repetição	sem repetição
com ordem	${ n^r}$	${ (n)_r }$
sem ordem	${ \binom {n+r-1}{r}}$	${\binom nr}$

9.9. Binômio de Newton

Se ${A}$ é um conjunto com ${n}$ elementos então a quantidade de subconjuntos de ${A}$ de cardinalidade ${r}$ é o número de maneiras distintas que podemos selecionar ${r}$ elementos dentre os ${n}$ do conjunto, isto é, são ${\binom nr}$ subconjuntos, como há ${2^n}$ subconjuntos de ${A}$ concluímos que

$\displaystyle \sum_{r=0}^n \binom nr = 2^n \ \ \ \ \ (61)$

Esse fato é consequência, também, de um resultado mais geral conhecido como Teorema Binomial.

Teorema 46 (Teorema Binomial) Para todo ${n>0}$ , vale

$\displaystyle (x+y)^n = \sum_{r=0}^n \binom nr x^r y^{n-r}.$

Fazendo ${x=y=1}$ temos a equação (61).

Vejamos como o produto de desenvolve para valores pequenos de ${n}$

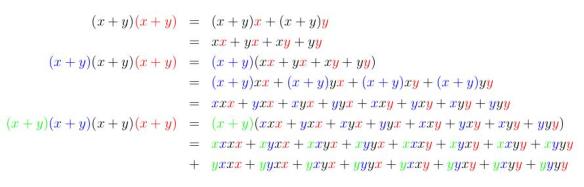
newton

Assim, ${(x+y)^n = }$

$\displaystyle (x+y)(x+y)\cdots (x+y) \ \ \ \ \ (62)$

com ${n}$ ocorrências de ${(x+y)}$ . Desenvolvendo o produto temos uma soma em que cada termo é da forma ${x^r y^{n-r}}$ , para ${0\leq r \leq n}$ . Para cada ${r}$ o coeficiente de ${x^r y^{n-r}}$ é o número de maneiras de escolher o ${x}$ de ${r}$ fatores da equação (62) (para o ${y}$ , dos ${n-r}$ fatores restantes). O número de maneiras de escolher ${r}$ fatores dentre ${n}$ é ${\binom nr}$ , portanto

$\displaystyle (x+y)^n = \sum_{r=0}^n \binom nr x^r y^{n-r}. \ \ \ \ \ (63)$

Exercício: Se ${A}$ , ${B}$ e ${C}$ são três subconjuntos de ${X=\{1,2,\dots,n\}}$ , prove que há ${7^n}$ ternas ${(A,B,C)}$ com ${A\cap B \subset C}$ .

[Solução]

Coeficiente multinomial

De volta ao exemplo mão de bridge, se dividimos a tarefa de distribuir as cartas em 4 etapas, cada etapa seleciona 13 cartas para um jogador, então pelo princípio multiplicativo o número de maneiras distintas de distribuir as cartas no jogo de bridge é

$\displaystyle \binom{52}{13} \binom{52-13}{13} \binom{52-13-13}{13} \binom{52-13-13-13}{13}= \binom{52}{13,13,13,13} \ \ \ \ \ (64)$

Com raciocínio análogo ao feito para o Teorema Binomial,

$\displaystyle (x+y+z)^n = \sum_{r_1+r_2+r_3=n} \binom n{r_1,r_2,r_3} x^{r_1} y^{r_2} z^{r_3}. \ \ \ \ \ (65)$

e, de modo geral,

Teorema 47 (Teorema Multinomial) Para todo ${n>0}$ , vale

$\displaystyle (x_1+x_2+\cdots+x_k)^n = \sum_{r_1+r_2+\cdots+r_k=n} \binom n{r_1,r_2,\dots,r_k} x_1^{r_1} x_2^{r_2}\cdots x_k^{r_k}.$

de modo que ${\binom n{r_1,r_2,\dots,r_k}}$ é conhecido como coeficiente multinomial.

Notas de aula

Jair Donadelli

[MCTB019-17] § 9 — Princípios de contagem: combinatória

Deixe um comentário Cancelar resposta

Compartilhe isso:

Relacionado

Deixe um comentário Cancelar resposta