[NHI2049-13 — Lógica Básica] Lógica de Predicados de Primeira Ordem – Linguagem

A lógica de primeira ordem é o padrão para a formalização axiomática da matemática. A Aritmética de Peano, por exemplo, e a Teoria de Conjuntos de Zermelo–Fraenkel são axiomatizações da Teoria dos Números e da Teoria de Conjuntos, respectivamente, na Lógica de Primeira Ordem. Os fundamentos da lógica de primeira ordem foram desenvolvidos de forma independente por Gottlob Frege e Charles Sanders Peirce.

6. Linguagens da lógica de primeira ordem

6.1. Discussão informal

O que queremos formalizar com a Lógica de predicados? Sentenças como

Todos os pássaros têm pena.
Nem todos os passáros voam.
Todos os pássaros são mais leves que algum mamífero.
Todo aluno é mais novo que algum professor.

podem ser simbolizadas no cálculo sentencial, mas o dito não captura toda estrutura da sentença. Os alvos do discurso (sujeito e objeto gramaticais) têm qualidade e mantêm relações. Além disso, os argumentos como

Premissa Todos os felinos são mamíferos

Premissa Alguns felinos são ferozes

Conclusão Alguns mamíferos são ferozes
Premissa Qualquer amigo de Maria é amigo de João

Premissa Pedro não é amigo de João

Conclusão Pedro não é amigo de Maria
Premissa O sucessor de um inteiro par é ímpar

Premissa 2 é um inteiro par

Conclusão O sucessor de 2 é ímpar
Premissa O quadrado de qualquer inteiro é positivo

Premissa 9 é um quadrado

Conclusão 9 é positivo

do ponto de vista da lógica proposicional são da forma ${\alpha \land \beta \rightarrow \gamma}$ que não são validados pela lógica proposicional.

O que procuramos? Uma linguagem mais rica que leva em conta a estrutura interna das sentenças

sujeito — predicado — objeto

na qual sujeito e objetos de quem se fala são elementos de um universo do discurso e são representados por constantes, por objetos genéricos e não especificados (pronomes) que são representados por variáveis; os predicados e as relações são explicitados. Incorpora o “para todo” e o “existe” como primitivas da linguagem.

Exemplo 30 Num universo (de discurso) far, far away ….
Constantes: ${a}$ para ‘Armando’, ${d}$ para ‘Daniel’ e ${j}$ para ‘Jair’.
Predicados: ${P}$ para ‘é professor’ e ${A}$ para ‘é aluno’.
Relações: ${J}$ para ‘lecionam juntos’ e ${N}$ para ‘é mais novo’. ${P(a)}$ simboliza a sentença ‘Armando é professor’. ${\neg A(j)}$ simboliza a sentença ‘Jair não é aluno’. ${J(a,d)}$ simboliza a sentença ‘Armando e Daniel lecionam juntos’. ${M(d,a)}$ simboliza a sentença ‘Daniel é mais novo que Armando’. Obervemos que, considerando o significado natural das sentenças, ${J(a,d)}$ e ${J(d,a)}$ têm o mesmo significado, mas ${M(a,d)}$ e ${M(d,a)}$ não têm o mesmo significado. Variáveis: usamos ${x,y,z\dots}$ para representar membros genéricos do universo. ${P(x)}$ simboliza ‘ ${x}$ é professor’ e ${M(x,y)}$ simboliza ‘ ${x}$ é mais novo que ${y}$ ‘. Nem ${P(x)}$ nem ${M(x,y)}$ têm valor lógico, não são sentenças no sentido da lógica proposicional vimos na Parte 1 destas notas. São chamadas de sentenças abertas. As sentenças abertas tornam-se sentenças lógicas quando substituímos as variáveis por constantes ou se quantificamos.
Quantificadores: o quantificador ${\forall}$ é lido “para todo” e o quantificador ${\exists}$ é lido “existe”.

${\forall x\, P(x)}$ simboliza a sentença ‘para todo ${x}$ , ${x}$ é professor’ a qual pode ser atribuída valor lógico: significa que todo elemento do universo do discurso é professor.

${\exists x \, P(x)}$ simboliza a sentença ‘existe ${x}$ , ${x}$ é professor’ a qual pode ser atribuída valor lógico: significa que pelo menos um elemento do universo do discurso é professor.

Notemos que, por exemplo

${\forall x \,M(x,y)}$ é uma sentença aberta
${\exists y\, \forall x\, M(x,y)}$ e ${ \forall x\, \exists y\,M(x,y)}$ têm significados diferentes.

A sentença ‘Todo aluno é mais novo que algum professor’ pode ser simbolizada por

$\displaystyle \forall x\,\exists y (A(x) \land P(y) \rightarrow M(x,y))$

A sentença ‘Há um professor tal que todo aluno aprende algo com ele’, considerando as relações ${B(x,y,z)}$ para ‘ ${y}$ aprende ${z}$ com ${x}$ ‘ e ${H(x)}$ para ‘ ${x}$ é um assunto’, pode ser simbolizada por

$\displaystyle \exists x\, \Big( P(x) \land \forall y\, \big( A(y) \rightarrow \exists z\, ( H(z) \land B(x,y,z) ) \big) \Big)$

Em matemática, muitas vezes tratamos de estruturas que consistem em um conjunto de elementos com várias operações sobre eles e relações entre eles. Por exemplo, na Teoria Elementar de Números o conjunto de elementos em discussão é o conjunto de números inteiros ${{\mathbb Z} = \{0, \pm 1, \pm2, \dots\}}$ Pode-se precisar de símbolos para alguns números, para variáveis, para funções (como ${\cdot}$ e ${+}$ ) e para as relações (como ${=}$ , ${<}$ , e ${|}$ ). A sentença “Para todo ${x}$ , se ${x}$ é inteiro igual a zero ou maior que zero e todo inteiro é divisível por ${x}$ , então ${x}$ é igual a um'' considerando que

${0}$ e ${1}$ são constantes;
${>\!(x,y)}$ simboliza a relação “ ${x}$ é maior que ${y}$ ”;
${=\!(x,y)}$ simboliza a relação “ ${x}$ é igual a ${y}$ ” e
${\mathrel{|}(x,y)}$ simboliza a relação “ ${x}$ divide ${y}$ ”,

é simbolizada como

$\displaystyle \forall x\, \Big( \big( >\!(x,0) \lor =\!(x,0) \big) \land \forall y\, ( \mathrel{|}(x,y) ) \,\rightarrow\, =\!(x,1)\Big) .$

Estruturas matemáticas

Uma estrutura matemática ${\mathfrak A}$ é dada por uma sequência

$\displaystyle \mathfrak A=(A, R_1 , \dots , R_n , F_1 , \dots, F_m , c_1,c_2,\dots,c_0)$

em que ${A}$ é um conjunto não vazio, ${R_1 , \dots , R_n}$ relações e ${F_1 , \dots, F_m }$ funções sobre ${A}$ e, finalmente, ${c_1,c_2,\dots,c_0}$ são constantes tomadas de ${A}$ . O conjunto ${A}$ é denominado domínio ou universo de ${\mathfrak A}$ . Um exemplo é ${(\{0, 1\}, \land, \lor, \neg)}$ . Aqui ${\land, \lor, \neg}$ têm seus significados habituais no domínio ${\{0, 1\}}$ , e não há relações ou constantes. Outro exemplo é ${({\mathbb N}, <, +, \cdot, 0, 1)}$ é um exemplo com universo ${{\mathbb N}}$ e ${<, +, \cdot, 0, 1}$ têm o seu significado usual. Também ${({\mathbb R}, +, \cdot, {}^{-1} , 0, 1)}$ é o corpo dos números reais e ${({\mathbb N}, <)}$ é o conjunto totalmente ordenado dos números naturais.

Se ${\mathfrak A}$ não contém funções ou constantes, então ${\mathfrak A}$ também é chamou de estrutura relacional, como em ${({\mathbb N}, <)}$ . Se ${\mathfrak A}$ não tem relações é chamado de estrutura algébrica, como em ${(\{0, 1\}, \land, \lor, \neg)}$ e em ${({\mathbb Z}, +, 0)}$ .

6.2. Linguagem formal da lógica de predicados

Há várias linguagens lógicas de primeira ordem, praticamente uma para cada assunto na matemática. Há símbolos comuns a todas e outros específicos (e.g., ${\in}$ , ${+}$ ). A seguir descrevemos a linguagem ${\mathcal L}$ genérica de primeira ordem.

Alfabeto genérico

Os símbolos permitidos para as expressões numa linguagem de primeira ordem incluem

Variáveis: ${x_1,x_2,x_3,\dots}$
Conectivos lógicos: ${\neg}$ , ${\rightarrow}$
Quantificador: ${\forall}$
Pontuação: abre parênteses, fecha parênteses e vírgula.
Símbolo de igualdade: ${=}$
Constantes: ${c_1,c_2,c_3,\dots}$
Símbolos relacionais: para cada inteiro ${n\geq 0}$ , temos os símbolos relacionais ${n}$ -ários ${R_1^n,R_2^n,R_3^n,\dots}$
Símbolos funcionais: para cada inteiro ${n\geq 1}$ , temos os símbolos funcionais ${n}$ -ários ${F_1^n,F_2^n,F_3^n,\dots}$

As constantes, os símbolos relacionais e funcionais são específicos de cada linguagem de primeira ordem e um ou mais deles pode ser vazio, isto é, o conjunto das constantes pode ser vazio, o conjuntos dos símbolos relacionais pode ser vazio e o conjunto símbolos funcionais pode ser vazio. Os símbolos relacionais de aridade ${0}$ são usados como símbolos proposicionais.

Os símbolos descritos nos quatros primeiros itens do alfabeto são os símbolos lógicos da linguagem. Os símbolos lógicos são compartilhados por toda linguagem de primeira ordem. O símbolo de igualdade é um símbolo relacional binário especial. Há autores que tratam a igualdade como um símbolo símbolo lógico e outros que tratam como não-lógico de modo a distinguir-se as linguagens de primeira ordem com igualdade e sem igualdade. Aqui não faremos essa distinção, não o chamaremos de lógico mas consideraremos que toda linguagem de primeira ordem tem o símbolo de igualdade. As constantes e os simbolos relacionais e funcionais são os símbolos não-lógicos da linguagem, os quais, geralmente, dependem do uso pretendido.

As constantes devem ser nomes para elementos particulares do universo da estrutura em discussão. Símbolos da função ${n}$ -ária são para funções específicas que mapeiam ${n}$ -úplas de elementos do universo da estrutura aos elementos do universo da estrutura. Símbolos de relação ${n}$ -ária destinam-se a designar relações particulares dentre ${n}$ elementos do universo da estrutura. O símbolo quantificador destina-se a representar “para todos” em referência à todos os elementos do universo e é usado usado com variáveis.

Termos:

são as cadeias finitas de símbolos do alfabeto obtidas a partir das regras

Constantes são termos.
Variáveis são termos.
Para qualquer natural ${n}$ , se ${t_1,t_2,\dots,t_n}$ são termos então ${F_i^nt_1t_2\dots t_n}$ é termo para todo ${i}$ .
Não há outros termos além dos obtidos pela aplicação das regras acima.

Exemplo 31 São termos: ${c_1}$ , ${x_{101}}$ , ${F_2^1x_1}$ , ${F_2^2x_1c_8}$ , ${F_1^4c_1c_2x_1x_2}$ . Note que ${F_2^2x_1}$ não é termo (por quê?).

A cadeia de símbolos ${F_1^1 F_1^2 x_1x_2}$ é um termo? ${F_1^1 F_1^2 F_1^1x_1x_2}$ é um termo?

Fórmulas:

ou fórmulas bem formadas, são as cadeias finitas de símbolos do alfabeto obtidas a partir das regras

Se ${t}$ e ${s}$ são termos, então ${ (=ts)}$ é uma fórmula. Também, para qualquer natural ${n}$ , se ${t_1,\dots,t_n}$ são termos então ${R_i^nt_1 t_2\dots t_n }$ é uma fórmula para todo ${i}$ . As fórmulas da linguagem obtidas por aplicação exclusiva dessa regra são ditas atômica.
Se ${\alpha}$ e ${\beta}$ são fórmulas, então ${(\neg\alpha)}$ e ${(\alpha \rightarrow \beta)}$ são fórmulas.
Se ${\alpha}$ é fórmula e ${x}$ é uma variável, então ${(\forall x\,\alpha)}$ é fórmula.
Não há outras fórmulas além daquelas obtidas pela aplicação das regras acima.

Exemplo 32 ${\Big(\big( R_1^1x_1 \rightarrow R_2^3x_4x_2c_1\big) \rightarrow \big(\forall x_1((\forall x_2\, R_2^3c_4x_2c_1) \rightarrow (\neg(=F_1^1x_1F_1^1c_1)))\big)\Big)}$ .

Simplificações, abreviaturas e omissão de parênteses

Vamos assumir algumas convenções de notação para facilitar nossa vida.

Simplificações

No uso dos símbolos admitimos algumas simplificações na escrita

Fórmulas: ${\alpha,\beta,\gamma,\dots}$ .
Termos: ${s,t,u,v}$ .
Variáveis: ${x,w,y,z}$ .
Constantes: ${a,b,c,d,e,f}$ .
Símbolos relacionais: Ao invés de ${R_i^n}$ escrevemos ${R}$ e também usamos outros símbolos como ${P,Q,R,S, < , \prec}$ . Ainda, ao invés de ${R^n t_1t_2\dots t_n}$ escrevemos ${R(t_1,t_2,\dots, t_n)}$ . Para as relações ${R}$ binárias escrevemos ${(a\mathrel{R}b)}$ ao invés de ${R(a,b)}$ , como em ${(a<b)}$ , em particular, escrevemos ${(t = s)}$ ao invés de ${=(t,s)}$ , como é usual.
Símbolos funcionais: Ao invés de ${F_i^n}$ escrevemos ${F}$ e também usamos outros símbolos como ${F,G,H,+,\cdot}$ . Ainda, ao invés de ${F^n t_1t_2\dots t_n}$ escrevemos ${F(t_1,t_2,\dots, t_n)}$ . Para as operações binárias ${F}$ escrevemos ${(a\mathop{F}b)}$ ao invés de ${F(a,b)}$ , como em ${(a+b)}$ .

Abreviaturas

Para resultados teóricos (metamatemáticos) é vantajoso possuirmos o mínimo possível de símbolos, entretanto, para expressarmos de maneira clara e sucinta quanto mais símbolos, melhor. Tratando alguns símbolos como abreviaturas de outros ganhamos dos dois lados.

símbolo	lê-se	uso
${\land}$	conjunção	${(\alpha \land \beta)}$ abrevia ${(\neg (\alpha \rightarrow (\neg\beta)))}$
${\lor}$	disjunção	${(\alpha \lor \beta)}$ abrevia ${((\neg \alpha)\rightarrow \beta)}$
${\leftrightarrow}$	bi-implica	${(\alpha \leftrightarrow \beta)}$ abrevia ${((\alpha \rightarrow \beta)\land (\beta \rightarrow \alpha))}$
${\exists}$	existe	${(\exists \,x \alpha)}$ abrevia ${(\neg(\forall\, x (\neg\alpha)))}$
${\nexists}$	não existe	${(\not\exists x\,\alpha)}$ abrevia ${(\neg(\exists \,x \alpha))}$ ou seja ${(\neg(\neg(\forall\, x (\neg\alpha))))}$
${\neq}$	diferente	${(s\neq t)}$ abrevia ${(\neg(s=t))}$
${\bot}$	falsum	abrevia ${(\alpha \land(\neg \alpha))}$
${\top}$	verum	abrevia ${(\neg \bot)}$

Ademais, representamos os conectivos lógicos ${\lor }$ , ${\land }$ , ${\rightarrow}$ e ${\leftrightarrow}$ genericamente, por ${\square}$ . Também, representamos os quantificadores ${\forall}$ e ${\exists}$ genericamente por ${\bigcirc}$ .

Omissão de parênteses

Omitimos os parênteses externos de uma fórmula, recolocando quando a usamos para compor outras fórmulas. Por exemplo, escrevemos ${\alpha\land \beta}$ no lugar de ${(\alpha\land \beta)}$ , mas recolocamos os parênteses quando escrevemos, por exemplo, ${\forall x(\alpha \land \beta)}$ .
${\forall}$ tem precedência sobre ${\neg}$ que tem precedência sobre ${\rightarrow}$ ; considerando as abreviações ordem de precedência é ${\forall , \exists , \neg , \land , \lor, \rightarrow , e \leftrightarrow}$ .
Em sequências de conjunções e em sequências de disjunções, omitimos o uso sucessivo de parênteses. Isto é, escrevemos ${\alpha \land \beta \land \gamma}$ no lugar de ${\alpha \land (\beta \land \gamma)}$ , o mesmo valendo para o conectivo ${\lor}$ . Conectivos são agrupados pela direita, por exemplo, ${ \alpha \rightarrow \beta \rightarrow \gamma}$ é lido como ${(\alpha \rightarrow (\beta \rightarrow \gamma))}$ .
Quando não houver riscos de más interpretações, omitimos os parênteses externos em subfórmulas do tipo ${\forall x\alpha}$ , ${\exists x\alpha}$ e ${\neg\alpha}$ . Por exemplo, escrevemos ${\neg\forall x\exists y\alpha}$ , em vez de ${\neg(\forall x(\exists y\alpha))}$ .

Exemplo 33 De volta ao exemplo 32

$\displaystyle \Big(\big( R_1^1x_1 \rightarrow R_2^3x_4x_2c_1\big) \rightarrow \big(\forall x_1((\forall x_2\, R_2^3c_4x_2c_1) \rightarrow (\neg(=F_1^1x_1F_1^1c_1)))\big)\Big)$

que simplificando fica escrito como

$\displaystyle (R(x) \rightarrow S(z,y,c)) \, \rightarrow \, \forall x\big(\forall y S(a,y,c) \rightarrow ( F(x) \neq F(c) ) \big) .$

6.6. Linguagens de primeira ordem para a Aritmética

Vejamos um exemplo de linguagem de primeira ordem para a Aritmética que consiste do estudo dos números naturais e suas propriedades. Denotaremos essa linguagem por ${\mathcal L_N}$ cujo alfabeto contém, além dos símbolos lógicos, os não-lógicos

a constante ${0}$ ,
o símbolo funcional unário ${S}$ e os símbolos funcionais binários ${+}$ e ${\cdot}$ e
o símbolo relacional binário ${<}$ .

São exemplos de termos dessa linguagem ${+\cdot 0x_1\,x_2}$ , ${SSSS0}$ , ${ +x_1S0}$ , ${=\cdot x_1+S0SS0\,\cdot x_1SSS0}$ . Usando as convenções de simplificação reescrevemo-os ${(0\cdot x)+y}$ , ${S(S(S(S(0))))}$ , ${ x+S(0)}$ , ${x\cdot (S(0)+S(S(0))) = x\cdot S(S(S(0)))}$ .

São fórmulas da linguagem:

${ < \cdot S0S0 \, + S0S0}$ ou, simplesmente, ${S(0)\cdot S(0) < S(0)+S(0)}$ .
${(\forall x_1\, =+ 0x_1x_1)}$ ou, simplesmente, ${\forall x (x+0 = x)}$ .
${\Big(\forall x_1\big(\forall x_2 ( = +S0x_1 +x_2S0 \rightarrow =x_1x_2 ) \big)\Big)}$ ou ${\forall x\,\forall y\, ( x+S(0) = y+S(0) \rightarrow x=y)}$ .
Já simplificado ${\forall x\,\forall y\, \exists z \, \big(y= x + z \rightarrow ( x<y \lor x = y)\big)}$ .

Os símbolos ${+,\cdot,<}$ intencionam ser interpretados pelas operações de adição e multiplicação em ${\mathbb N}$ e a relação 'menor que' em ${\mathbb N}$ , respectivamente, e $S$ intenciona ser interpretada pela função sucessor.
Os termos ${0,S0,SS0,SSS0,SSSS0,\dots}$ intencionam descrever os números naturais zero, um , dois, três, quatro, etc.
Com essa interpretação, que ainda é uma intenção, ela só vai ser dada
quando falarmos da semântica, podemos dar alguns exemplos intuitivos da
expressão da aritmética nessa linguagem.

Exemplo 34 ‘Não existe raiz de 2’ é expresso por ${\nexists x (x \cdot x = S(S(0)))}$ que reescrita usando somente símbolos do alfabeto fica ${(\neg (\neg (\forall x_1(\neg (= \cdot x_1 x_1 SS0)))))}$ . Também podemos expressar a mesma ideia usando ${(\forall x_1 (\neg (= \cdot x_1 x_1 SS0) ) )}$ .

Exercício:
Expresse em ${\mathcal L_N}$ a sentença ‘existem infinitos números primos’.

6.7. Outros exemplos de linguagens de primeira ordem

Uma linguagem de primeira ordem tem os símbolos lógicos (comum às linguagens) e os símbolos extralógicos (específicos de cada linguagem). Abaixo, para definir uma linguagem explicitamos só os símbolos extralógicos.

Exemplo 35 A linguagem da igualdade pura, ${\mathcal L_=}$ :

Não há símbolos não-lógicos.

Ainda assim conseguimos expressar certas ideias, por exemplo, ‘existe um único sujeito’ ${\exists x\, \forall y (y=x)}$ , ou ‘existem somente dois sujeitos’ ${\exists x\,\exists y( (x\neq y) \land \forall z\,(z=x \lor z=y))}$ .

Exemplo 36 Uma linguagem para Teoria dos Conjuntos ${\mathcal L_{C}}$ :

Símbolo relacional binário: ${\in}$

A intenção das variáveis é representar conjuntos e ${x\in y}$ diria que o conjunto ${x}$ é elemento do conjunto ${y}$ . A Teoria de Conjuntos de Zermelo–Fraenkel é escrita nessa linguagem. A existência do conjunto vazio é expressa por ${\exists x\,\forall y \neg(y\in x)}$ . A existência do conjunto definido no paradoxo de Russel é expresso por ${\exists x\,\forall y\, ( y\in x \leftrightarrow \neg(y\in y))}$ . Veremos que a negação dessa sentença é uma tautologia.

Exemplo 37 Uma linguagem para a Teoria dos Grupos tem uma constante, denotada por ${\mathrm{e}}$ , e uma função binária, denotada por ${\circ}$ . Essa teoria é a coleção dos teoremas que podem ser provados a partir dos seguintes axiomas

(G1): ${\forall x\,((x \circ {e} = x) \land ({e} \circ x = x))}$ ;
(G2): ${\forall x \exists y\,(x \circ y = {e})}$ ;
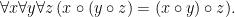
(G3): ${\forall x\forall y\forall z\,(x \circ (y \circ z) = (x \circ y) \circ z).}$

6.8. Variáveis livres e ligadas

Dizemos que uma variável ${x}$ ocorre livre em uma fórmula ${\alpha}$ se

${\alpha}$ é atômica e ${x}$ ocorre em ${\alpha}$ ;
${\alpha}$ é da forma ${(\neg \beta)}$ e ${x}$ ocorre livre em ${\beta}$ ;
${\alpha}$ é da forma ${(\beta \square \gamma)}$ e ${x}$ ocorre livre em ${\beta}$ ou ${\gamma}$ ;
${\alpha}$ é da forma ${\bigcirc y \psi}$ e ${x}$ é diferente de ${y}$ e ${x}$ ocorre livre em ${\psi}$ .

Uma ocorrência de ${x}$ em ${\alpha}$ que não é livre é dita ligada. O item 4 acima é a chave para classificarmos a ocorrência de uma variável como livre ou ligada: a ocorrência de uma variável ${x}$ é ligada se ela está no escopo de uma ocorrência de um quantificador. O escopo de um quantificador numa fórmula ${\alpha}$ é a subfórmula ${\beta}$ na qual o quantificador se aplica (quando a regra de formação de fórmula quantificada foi aplicada, isto é, em ${(\forall x\,\beta)}$ o escopo de ${x}$ é ${\beta}$ ).

Cada ocorrência de uma variável ${x}$ é livre ou ligada, mas não ambas. Entretanto, a variável pode ocorrer livre e ligada na mesma fórmula. Por exemplo,

Em ${\forall x_7 (x_5=x_7)}$ a ocorrência de ${x_5}$ é livre e a ocorrência de ${x_7}$ é ligada.
Em ${\forall x_0\, ( (x_0 = F(x_6)) \rightarrow (\neg\forall x_6\, R(x_6)))}$ a primeira ocorrência de ${x_6}$ é livre e a última ocorrência é ligada.
Em ${\forall z\, (\forall x\, ( P(x) \rightarrow R(z) ) ) \rightarrow (Q(y)\rightarrow P(x))}$ a variável ${x}$ é livre e ligada, ${y}$ é livre e ${z}$ é ligada.

Uma fórmula ${\alpha}$ sem ocorrência de variáveis livre é dita sentença.

6.9. Substituição de variáveis

Se ${t}$ e ${s}$ são termos e ${x}$ é uma variável, definimos ${[t]^s_x}$ o termo obtido substituindo toda ocorrência da variável ${x}$ pelo termo ${s}$ . Formalmente, definimos a substituição em termos recursivamente:

${[x]^s_x}$ é o termo ${s}$ ;
se ${c}$ é uma constante, ${[c]^s_x}$ é o termo ${c}$ ;
se ${v}$ é uma variável diferente de ${x}$ , ${[v]^s_x}$ é o termo ${v}$ ;
se ${t}$ é da forma ${F (t_1 ,\dots, t_n )}$ , então ${[t]^s_x}$ é o termo ${F ([t_1]^s_x ,\dots, [t_n ]^s_x )}$ .

Se ${\alpha}$ é uma fórmula, ${x}$ é uma variável e ${t}$ é um termo, definimos ${[\alpha]^t_x}$ a fórmula obtida substituindo todas as ocorrências livres da variável ${x}$ pelo termo ${t}$ .

Formalmente, definimos a substituição em fórmulas recursivamente:

se ${\alpha}$ é ${(s=t)}$ então ${[\alpha]_x^t}$ é ${([s]_x^t=[t]_x^t)}$ ;
Se ${\alpha}$ é ${R(t_1, t_2,\dots, t_n) }$ então ${[\alpha]_x^t}$ é ${R([t_1]_x^t, [t_2]_x^t,\dots, [t_n]_x^t) }$ ;
Se ${\alpha}$ é ${\neg\beta}$ então ${[\alpha]_x^t}$ é ${\neg[\beta]_x^t}$ ;
Se ${\alpha}$ é ${\gamma \rightarrow \beta}$ então ${[\alpha]_x^t}$ é ${[\gamma]_x^t \rightarrow [\beta]_x^t}$ ;
Se ${\alpha}$ é ${\forall x\,\beta }$ então ${[\alpha]_x^t}$ é ${\alpha}$ e se ${\alpha}$ é ${\forall y\,\beta }$ então ${[\alpha]_x^t}$ é ${\forall y\,[\beta]_x^t }$ sempre que ${y\neq x}$ .

Por exemplo:

${[(x = y)]_y^x}$ é ${(x = x)}$ .
${[(x = y)]_x^y}$ é ${(y = y)}$ .
${[\forall x\,(x = y)]_x^y}$ é ${\forall x\,(x = y)}$ .
${[\forall x\, (x = y)]_y^x}$ é ${\forall x\,(x = x)}$ .
${[(\forall x\, P(x)) \rightarrow P(x)]_x^\tau}$ é ${\forall x\,P(x) \rightarrow P(\tau)}$ .
${[\forall x\,(\neg\forall y \,(x = y)) \rightarrow (\neg \forall y\,(x = y))]_x^y}$ é ${\forall x\,(\neg\forall y \,(x = y)) \rightarrow (\neg \forall y\,(y = y))}$ .
${[\forall x\, (P(x, y) \rightarrow (\neg Q(y) \lor \exists y\,P(x, y)))]^{F(y,z)}_y}$ é ${\forall x\, (P(x, F(y,z)) \rightarrow (\neg Q(F(y,z)) \lor \exists y\,P(x, y)))}$ .

Exemplo 38 Considere em ${\mathcal L_N}$ a fórmula ${\exists x (y = S(S(0)) \cdot x)}$ para ‘ ${y}$ é par’. Se substituímos ${y}$ pelo termo ${S(S(S(0)))}$ temos ${\exists x \,(S(S(S(0))) = S(S(0)) \cdot x)}$ , Se substituímos por ${x}$ temos ${\exists x (x = S(S(0)) \cdot x)}$

6.10. Metateoremas de leitura única e indução

Metateorema 39 (Teorema da unicidade de representação dos termos) Se ${t}$ é um termo de uma linguagem, então uma, e apenas uma, das asserções abaixo é verdadeira:

${t}$ é uma variável;
${t}$ é uma constante;
${t}$ é da forma ${F (t_1 ,\dots, t_n )}$ , onde ${t_1 ,\dots, t_n}$ são termos e ${F}$ é um símbolo funcional ${n}$ -ário.

Além disso, se ${t}$ é da forma ${F (t_1 ,\dots, t_n )}$ e, ao mesmo tempo, é da forma ${G (s_1 ,\dots, s_m )}$ então:

${n = m}$ ;
${F}$ e ${G}$ são o mesmo símbolo funcional;
${t_i}$ é o mesmo termo que ${s_i}$ , para todo ${i \leq n}$ .

Metateorema 40 (Teorema da unicidade de representação das fórmulas) Seja ${\alpha}$ uma fórmula de uma linguagem. Então ${\alpha}$ satisfaz uma, e apenas uma, das condições abaixo

${\alpha}$ é uma fórmula atômica da forma ${R(t_1 ,\dots, t_n )}$ , onde ${R}$ é um símbolo relacional ${n}$ -ário e ${t_1 ,\dots, t_n }$ são termos;
${\alpha}$ é uma fórmula atômica da forma ${(s = t)}$ onde ${s}$ e ${t}$ são termos;
${\alpha}$ é da forma ${\neg\beta}$ , para uma única fórmula ${\beta}$ ;
${\alpha}$ é da forma ${\beta \rightarrow \gamma}$ para únicos ${\beta}$ e ${\gamma}$ fórmulas;
${\alpha}$ é da forma ${\forall x\beta}$ , para uma única fórmula ${\beta}$ e uma única variável ${x}$ .

Além disso, valem:

${\alpha}$ é é da forma ${(s = t)}$ e, ao mesmo tempo, é da forma ${(u=v)}$ então ${s}$ é o mesmo que ${u}$ e ${t}$ é o mesmo que ${v}$ ;
se ${\alpha}$ é da forma ${R (t_1 ,\dots, t_n )}$ e, ao mesmo tempo, é da forma ${S (s_1 ,\dots, s_m )}$ então:

${n = m}$ ;
${R}$ e ${S}$ são o mesmo símbolo relacional;
${t_i}$ é o mesmo termo que ${s_i}$ , para todo ${i \leq n}$ .

Metateorema 41 (Princípio de indução para termos) Seja ${\Gamma}$ um conjunto de termos de uma linguagem de primeira ordem ${\mathcal L}$ e suponha que

as variáveis e as constantes de ${\mathcal L}$ pertencem a ${\Gamma}$ ;
se ${t_1,t_2,\dots t_n}$ pertencem a ${\Gamma}$ então ${F(t_1,t_2,\dots t_n)}$ pertencem a ${\Gamma}$ para qualquer que seja o símbolo funcional ${F}$ .

Então ${\Gamma}$ é o conjunto de todas as fórmulas da linguagem.

Metateorema 42 (Princípio de indução para as fórmulas) Seja ${\Gamma}$ um conjunto de fórmulas de uma linguagem de primeira ordem ${\mathcal L}$ e suponha que

as fórmulas atômicas de ${\mathcal L}$ pertencem a ${\Gamma}$ ;
se ${\alpha}$ pertence a ${\Gamma}$ então ${\neg\alpha}$ pertence a ${\Gamma}$ ;
se ${\alpha}$ e ${\beta}$ pertencem a ${\Gamma}$ então ${\alpha\rightarrow\beta}$ pertence a ${\Gamma}$ ;
se ${\alpha}$ pertence a ${\Gamma}$ e ${x}$ é uma variável, então ${\forall x\,\alpha}$ pertence a ${\Gamma}$ .

Então ${\Gamma}$ é o conjunto de todas as fórmulas da linguagem.

Notas de aula

Jair Donadelli

[NHI2049-13 — Lógica Básica] Lógica de Predicados de Primeira Ordem – Linguagem

Deixe um comentário Cancelar resposta

Premissa	Todos os felinos são mamíferos
Premissa	Alguns felinos são ferozes
Conclusão	Alguns mamíferos são ferozes

Premissa	Qualquer amigo de Maria é amigo de João
Premissa	Pedro não é amigo de João
Conclusão	Pedro não é amigo de Maria

Premissa	O sucessor de um inteiro par é ímpar
Premissa	2 é um inteiro par
Conclusão	O sucessor de 2 é ímpar

Premissa	O quadrado de qualquer inteiro é positivo
Premissa	9 é um quadrado
Conclusão	9 é positivo

Compartilhe isso:

Relacionado

Deixe um comentário Cancelar resposta