[NHI2049-13 — Lógica Básica] Lógica de Predicados de Primeira Ordem – Sistema dedutivo

Publicado em por

São conhecidos alguns sistemas dedutivos para o cálculo de predicados que são equivalentes no sentido de deduzirem os mesmos teoremas. Apresentaremos um Sistema axiomático à Hilbert para a linguagem {\mathcal L} da lógica de primeira ordem. Tal sistema é axiomático, consiste numa lista finita de axiomas e outra de regras de inferência que podem ser usados para derivar os teoremas do sistema.

Variáveis livres

Antes de irmos adiante, definimos recursivamente o conjunto {VL} das variáveis livres de uma fórmula:

  1. se {t} é termo então

    \displaystyle VL(t):= \begin{cases} \emptyset, & \text{ se } t \text{ \'e } c\\ \{x\}, & \text{ se } t \text{ \'e } x\\ VL(t_1)\cup \cdots\cup VL(t_n), & \text{ se } t \text{ \'e } F(t_1,\dots,t_n) \end{cases}

  2. se {\alpha} é fórmula então

    \displaystyle VL(\alpha):= \begin{cases} VL(t_1)\cup VL(t_2), & \text{ se } \alpha \text{ \'e } t_1=t_2 \\ VL(t_1)\cup \cdots\cup VL(t_n), & \text{ se } \alpha \text{ \'e } R(t_1,\dots,t_n) \\ VL(\beta) , & \text{ se } \alpha \text{ \'e } \neg\beta\\ VL(\beta)\cup VL(\gamma), & \text{ se } \alpha \text{ \'e } \beta \square \gamma\\ VL(\beta)\setminus \{x\} , & \text{ se } \alpha \text{ \'e } \forall x\,\beta\text{ ou } \exists x\,\beta \end{cases}

Lembremos que se {\varphi} é uma fórmula, {x} uma variável e {t} um termo, então {[\varphi]^t_x} é a fórmula que obtemos depois de substituir todas as ocorrências livres da variável {x} por {t}; esse processo é chamado de substituição.

Agora, a substituição da variável {x} pelo termo {t} na fórmula {\varphi} é admissível se nenhuma ocorrência livre de {x} em {\varphi} estiver no escopo de um quantificador que liga qualquer variável que aparece em {t}. Isto é, para cada variável {y} que aparece em {t}, nenhum lugar onde {x} ocorre livre em {\varphi} está no escopo de ‘{\exists y}‘ ou ‘{\forall y}‘.

Por exemplo, se {x \not\in VL (\varphi)}, então {[\varphi]_x^t} é admissível para qualquer termo {t} e, nesse caso, as fórmulas {\varphi} e {[\varphi]_x^t} são idênticas. Uma variável {x} sempre é admissível para ela mesmo em qualquer fórmula e {[\varphi]_x^x} é a fórmula {\varphi}. A variável {y} não é uma substituição admissível para {x} na fórmula {\forall y\, (x=y)} porque se substituímos {x} por {y} a nova ocorrência de {y} seria ligada. Isso fará diferença no valor verdade de uma sentença, enquanto que {\forall y\, (y=y)} será uma tautologia em qualquer interpretação, a fórmula {\forall y\, (x=y)} tem valor verdade que dependerá da interpretação.

É {x} uma substituição admissível para {z} em {\varphi} se {\varphi} é {z = x \rightarrow \forall z\, (z = x)}? Em caso afirmativo, o que é {[\varphi]^x_z}?

Generalização

Se {\alpha} é uma fórmula então uma generalização de {\alpha} é a fórmula

\displaystyle \forall x_1\forall x_2\cdots\forall x_n \, \alpha

para quaisquer coleção de variáveis {x_1,x_2,\dots,x_n}, independente delas ocorrerem ou não em {\alpha}.

Exemplo 43 São generalizações de {x=y} as fórmulas: {\forall x\,(x=y)}, {\forall y\,(x=y)}, {\forall y\forall x\,(x=y)}, {\forall z \forall y\forall x\,(x=y)}, {\forall w\forall z \forall y\forall x\,(x=y)}.

Esquemas de axiomas e de teoremas

No que segue, chamaremos de axioma, por exemplo

\displaystyle \alpha \rightarrow (\beta \rightarrow \alpha)

e

\displaystyle \forall x\,(\alpha \rightarrow \beta) \rightarrow (\alpha \rightarrow \forall x\,\beta)

o que, propriamente, não são como já usamos usamos na lógica proposicional. São esquemas de axiomas e de teoremas pois usam variáveis da metalinguagem. Os axiomas são obtidos quando substituímos tais variáveis por fórmulas nas quais figuram apenas símbolos do alfabeto de modo que toda ocorrência da mesma (meta)variável é substituída pela mesma fórmula.

7.1. Axiomas

Um sistema dedutivo para uma linguagem de primeira ordem tem duas classes de axiomas, os lógicos comuns a todas as linguagens e os não-lógicos específicos da teoria.

Os axiomas não-lógicos são os axiomas específicos das teorias, como os axiomas G1, G2 e G3 da Teoria dos Grupos do exemplo 37.

Os axiomas lógicos são:

  • (A0) {\alpha \rightarrow \alpha}
  • (A1) {\alpha \rightarrow (\beta\rightarrow\alpha)}
  • (A2) {(\alpha \rightarrow (\beta\rightarrow\xi)) \rightarrow ((\alpha\rightarrow\beta) \rightarrow (\alpha\rightarrow\xi))}
  • (A3) {(\alpha \rightarrow \beta) \rightarrow ((\alpha \rightarrow \neg\beta) \rightarrow \neg\alpha)}
  • (A4) {{ \alpha \rightarrow( \beta \rightarrow (\alpha \land \beta)) }}
  • (A5) {{ \alpha \land \beta \rightarrow \alpha }}
  • (A6) {{ \alpha \land \beta \rightarrow \beta }}
  • (A7) {{ \alpha \rightarrow \alpha \lor \beta }}
  • (A8) {{ \beta \rightarrow \alpha \lor \beta }}
  • (A9) { { (\alpha \rightarrow \gamma )\rightarrow ((\beta \rightarrow \gamma )\rightarrow (\alpha \lor \beta \rightarrow \gamma)) } }
  • (A10) {\neg\alpha \rightarrow (\alpha\rightarrow\beta)}
  • (A11) {(\forall x\, (\alpha \rightarrow \beta))\rightarrow (\forall x\,\alpha \rightarrow \forall x \,\beta)}.
  • (A12) {(\forall x\,\alpha) \rightarrow [\alpha]^t_x} sempre que {t} é admissível para {x} em {\alpha}.
  • (A13) { \alpha \rightarrow \forall x\, \alpha} sempre que {x\not\in VL(\alpha)}.
  • (A14) {t = t}
  • (A15) {t_1=t_2 \rightarrow t_2=t_1}
  • (A16) {(t_1=t_2 \land t_2=t_3) \rightarrow t_1=t_3}
  • (A17) {(t_1 = t_1' \land \cdots \land t_n = t_n' ) \rightarrow \big(R(t_1 , \dots,t_n ) \rightarrow R(t_1' ,\dots, t_n' )\big)}
  • (A18) {(t_1 = t_1' \land \cdots \land t_n = t_n' ) \rightarrow \big(F(t_1 , \dots,t_n ) = F(t_1' ,\dots, t_n' )\big)}

em que {\alpha, \beta,\gamma,\xi} são fórmulas, {x} é variável, {t} e {t_1,t_2,t_3,\dots, t_n} são termos da linguagem {\mathcal L}.

Exemplo 44 Caso não houvesse restrição sobre a substituição de variável, é possível (e.g., numa interpretação onde o universo tem mais de um elemento) que a fórmula {\forall x \, \exists y\, (x \neq y)} seja válida. De (AQ) incondicional teríamos o axioma {\forall x \, \exists y\, (x \neq y) \rightarrow [\exists y\, (x \neq y)]_y^x}, ou seja, teríamos o axioma {\forall x \, \exists y\, (x \neq y) \rightarrow \exists y\, (y \neq y)} que,intuitivamente, deveria ser falso.

Exemplo 45 Temos que

\displaystyle \neg P(x) \rightarrow ( P(x) \rightarrow \neg\forall y\, \neg P(y))

é uma instância de {\neg\alpha \rightarrow (\alpha\rightarrow\beta)} portanto é um axioma do esquema (A10). A fórmula

\displaystyle (R(x,y) \rightarrow (\exists y\,(y = 0) \lor R(x,y))

é uma instância de {\beta \rightarrow (\alpha \lor \beta)}, portanto é um axioma do esquema (A8).

Ademais, as generalizações desses axiomas, como

\displaystyle \forall x \,\big(\neg P(x) \rightarrow ( P(x) \rightarrow \neg\forall y\, \neg P(y))\big)

\displaystyle \forall y \,\big(\neg P(x) \rightarrow ( P(x) \rightarrow \neg\forall y\, \neg P(y))\big)

\displaystyle \forall x \forall y \,\big(\neg P(x) \rightarrow ( P(x) \rightarrow \neg\forall y\, \neg P(y))\big)

são teoremas devido à regra de generalização.

Exemplo 46 A fórmula

\displaystyle \forall x\, \big ( \neg \forall y\, (x=y) \big)\rightarrow \big( \neg \forall y\, (z=y) \big)

é um axioma do esquema (AQ). Também é a fórmula

\displaystyle \forall x\, (A(x) \rightarrow \forall y\,A(y)) \rightarrow (A(y) \rightarrow \forall y\,A(y))

porém a fórmula

\displaystyle \forall x\,\big( \forall y\, B(x,y ) \big) \rightarrow \forall y\,B(y,y))

não é um axioma desse esquema porque viola a condição de admissibilidade.

A fórmula {(x = y) \rightarrow ((x + x = 0) \rightarrow (x + y = 0))} é um axioma do esquema (A3I)?

7.2. Regras de inferência

As regras de inferência (de fato esquemas) do sistema são

Modus Ponens (MP): se então {\alpha} é teorema e {\alpha\rightarrow\beta} é teorema, então {\beta} é teorema.

\displaystyle \frac{\alpha,~\alpha\rightarrow\beta}{\beta}

Generalização (G): se {\alpha} é teorema então {\forall x\, \alpha} é teorema.

\displaystyle \frac{\alpha}{\forall x\, \alpha}

7.3. Teorema e Prova

Teorema é qualquer fórmula para a qual existe uma prova a partir dos axiomas lógicos e regras de inferência. Observemos que qualquer fórmula que ocorre numa prova formal de um teorema também é um teorema. Axioma também é um teorema.

Sejam {\alpha} uma fórmula da linguagem de primeira ordem {\mathcal L} e {\Gamma \subset \mathcal L} (em geral são sentenças) um conjunto de hipóteses ou premissas. Uma prova de {\alpha} a partir de {\Gamma} é uma sequência finita de fórmulas

\displaystyle \langle \varphi_1,\varphi_2,\dots,\varphi_n \rangle

tal que {\varphi_n= \alpha} e, para {i<n}, {\varphi_i} é

  1. ou um axioma lógico
  2. ou uma fórmula de {\Gamma}
  3. ou uma fórmula obtida de {\varphi_1,\varphi_2,\dots,\varphi_{i-1}} por regra de inferência.

{\Gamma\vdash \alpha} e lê-se “{\alpha} é deduzível de {\Gamma}”, ou “{\Gamma} prova {\alpha}”, ou {\alpha} é consequência sintática de {\Gamma}.

No caso {\Gamma} vazio escrevemos {\vdash \alpha} e, nesse caso, {\alpha} é um {teorema}.

Simplificações de notação:

  • Ao invés de {\{\alpha\} \vdash \beta} escrevemos {\alpha \vdash \beta} .
  • Ao invés de {\{\alpha_1,\dots,\alpha_n\} \vdash \beta} escrevemos {\alpha_1,\dots,\alpha_n \vdash \beta} .

  • Ao invés de {\Gamma \cup \{\alpha\} \vdash \beta} escrevemos {\Gamma, \alpha \vdash \beta} .

Propriedades de {\vdash}

As seguintes propriedades valem exatamente como na lógica de proposições.

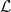
Metateorema 47 Se {\Gamma} é um conjunto de fórmulas de {\mathcal L}

  1. {\Gamma \vdash \alpha} para todo {\alpha \in \Gamma}.
  2. Se {\Gamma \vdash \alpha} e {\Sigma \supseteq \Gamma} então {\Sigma \vdash \alpha}.
  3. Se {\Gamma \vdash \alpha_i} {(i=1,2,\dots,k)} e {\{\alpha_1,\dots,\alpha_k\} \vdash \beta} então~{\Gamma\vdash\beta}.
  4. Regra do destacamento: Se {\Gamma \vdash \alpha} e {\Gamma\vdash \alpha\rightarrow\beta} então~{\Gamma\vdash \beta}.
  5. Teorema da Dedução: se nas provas não for usado a regra de generalização,

    \displaystyle \Gamma\vdash \alpha\rightarrow\beta \text{ se e s\'o se } \Gamma, \alpha \vdash \beta.

Deduzir um teorema a partir da lista de axiomas pode não ser uma tarefa fácil. Porém, cada vez que provamos um teorema, podemos colocá-lo diretamente dentro de uma outra dedução sem precisarmos prová-lo novamente. Na prática, eles funcionam como novos axiomas e regras de inferências que deduzimos, e, a partir de então, podemos utilizá-los nas próximas deduções.

Teorema 8 {\alpha \vdash \alpha}

Prova: Segue de (A0) e do Teorema da Dedução. \Box

Teorema 9 (Redução ao absurdo (RA)) {\alpha\rightarrow\beta}, {\alpha\rightarrow\neg\beta \vdash \neg\alpha}

Prova: Segue do Teorema da Dedução em (A3). \Box

Teorema 10 (Introdução da conjunção (IC)) {\alpha}, {\beta \vdash \alpha \land \beta}

Prova: Segue do Teorema da Dedução em (A4). \Box

Teorema 11 (Eliminação da conjunção (EC1)) {\alpha \land\beta \vdash \alpha }

Prova: Segue do Teorema da Dedução em (A5). \Box

Teorema 12 (Eliminação da conjunção (EC2)) {\alpha \land\beta \vdash \beta }

Prova: Segue do Teorema da Dedução em (A6). \Box

Teorema 13 (Introdução da disjunção (ID1)) {\alpha \vdash \alpha \lor \beta}

Prova: Segue do Teorema da Dedução em (A7). \Box

Teorema 14 (Introdução da disjunção (ID2)) {\beta \vdash \alpha \lor \beta}

Prova: Segue do Teorema da Dedução em (A8). \Box

Teorema 15 (Duns Scotus (DS)) {\alpha}, {\neg\alpha \vdash \beta}

Prova: Segue do Teorema da Dedução em (A10). \Box

Teorema 16 (Instanciação universal (IU)) { \forall x\, \alpha \vdash [\alpha]_x^t}, para todo termo {t} admissível para {x}.

Prova: Segue do Teorema da Dedução em (A12). \Box

Teorema 17 (Generalização universal (G)) {\alpha \vdash \forall x\, \alpha}, se {x\not\in VL(\alpha)}.

Prova: Segue do Teorema da Dedução em (A13). \Box

Teorema 18 (Modus Tollens (MT)) {\alpha\rightarrow\beta ,\neg\beta \vdash \neg\alpha}

Prova:

1. {\alpha\rightarrow\beta} (hip.)
2. {\neg\beta} (hip.)
3. {(\alpha\rightarrow\beta)\rightarrow((\alpha\rightarrow\neg\beta)\rightarrow\neg\alpha)} (A3)
4. {\neg\beta\rightarrow (\alpha\rightarrow\neg\beta)} (A1)
5. {\alpha\rightarrow\neg\beta} (MP 2,4)
6. {(\alpha\rightarrow\neg\beta)\rightarrow\neg\alpha} (MP 1,3)
7. {\neg\alpha} (MP 5,6)

\Box

Teorema 19 (Contra-positiva (CP1)) { \alpha\rightarrow\beta \vdash \neg\beta \rightarrow \neg\alpha}

Prova: Segue de Modus Tollens por aplicação do Teorema da Dedução. \Box

Teorema 20 (Silogismo hipotético (SH)) {\alpha \rightarrow \beta, \beta \rightarrow \gamma \vdash \alpha \rightarrow \gamma}

Prova:

1. {\alpha \rightarrow \beta} (hipótese)
2. { \beta \rightarrow \gamma} (hipótese)
3. {(\beta\rightarrow\gamma)\rightarrow(\alpha\rightarrow(\beta\rightarrow\gamma))} (A1)
4. {(\alpha\rightarrow(\beta\rightarrow\gamma)} (MP 2,3)
5. {(\alpha\rightarrow(\beta\rightarrow\gamma))\rightarrow ((\alpha\rightarrow\beta)\rightarrow(\alpha\rightarrow\gamma))} (A2)
6. {(\alpha\rightarrow\beta)\rightarrow(\alpha\rightarrow\gamma)} (MP 4,5)
7. {\alpha\rightarrow\gamma} (MP 1,6)

\Box

Teorema 21 (Silogismo disjuntivo (SD)) {\alpha \lor \beta}, {\neg\alpha \vdash \beta}

Prova:

1. {\alpha \lor \beta} (hip.)
2. {\neg\alpha \rightarrow \beta} (reescrita de 1)
3. { \neg \alpha} (hip.)
4. {\beta} (MP 2,3)

\Box

Teorema 22 (Troca condicional (TC)) {\theta \rightarrow(\phi \rightarrow \xi) \vdash \phi \rightarrow(\theta\rightarrow\xi)}

Prova:

1. {\theta \rightarrow(\phi \rightarrow \xi)} (hipótese)
2. {(\theta \rightarrow(\phi \rightarrow \xi)) \rightarrow ((\theta\rightarrow\phi)\rightarrow(\theta\rightarrow\xi))} (A2)
3. {(\theta\rightarrow\phi)\rightarrow(\theta\rightarrow\xi)} (MP 1,2)
4. {\phi\rightarrow(\theta\rightarrow\phi)} (A1)
5. {((\theta\rightarrow\phi)\rightarrow(\theta\rightarrow\xi))\rightarrow(\phi\rightarrow((\theta\rightarrow\phi)\rightarrow(\theta\rightarrow\xi)))} (A1)
6. {(\phi\rightarrow((\theta\rightarrow\phi)\rightarrow(\theta\rightarrow\xi))} (MP 3,5)
7. {(\phi\rightarrow((\theta\rightarrow\phi)\rightarrow(\theta\rightarrow\xi)))\rightarrow ((\phi\rightarrow(\theta\rightarrow\phi))\rightarrow(\phi\rightarrow(\theta\rightarrow\xi)))} (A2)
8. {(\phi\rightarrow(\theta\rightarrow\phi))\rightarrow(\phi\rightarrow(\theta\rightarrow\xi))} ( MP 6,7)
9. {\phi\rightarrow(\theta\rightarrow\xi)} (MP 4,5)

\Box

Teorema 23 (Dupla negação (DN1)) {\neg\neg\alpha \vdash \alpha }.

Prova:

1. {\neg\neg\alpha} (hipótese)
2. {\neg\neg\alpha\rightarrow(\neg\alpha\rightarrow\alpha)} (A10)
3. {\neg\alpha\rightarrow\alpha} (MP 1,2)
4. {(\neg\alpha\rightarrow\alpha) \rightarrow ((\neg\alpha\rightarrow \alpha)\rightarrow(\alpha \lor \neg \alpha \rightarrow\alpha))} (A9)
5. {(\neg\alpha\rightarrow \alpha)\rightarrow(\alpha \lor \neg \alpha \rightarrow\alpha)} (MP 3,4)
5. {\alpha \lor \neg \alpha \rightarrow\alpha} (MP 3,5)
5. {(\neg\alpha \rightarrow \neg \alpha) \rightarrow\alpha} (definição de {\lor})
6. {\neg\alpha\rightarrow\neg\alpha} (A0)
7. {\alpha} (MP 5,6)

\Box

Regras de inferências derivadas

Agora podemos levar as abreviaturas um passo adiante. Uma regra de inferência derivada é uma regra de inferência não dada a nós como parte do sistema dedutivo, mas que constitui uma abreviatura usando um teorema previamente comprovado. Em particular, suponha que tenhamos {\Gamma\vdash\alpha} com {\Gamma=\{\gamma_1,\dots,\gamma_k\}} um conjunto finito de teoremas. Então sempre que deduzimos, digamos numa prova de {\Sigma\vdash\beta}, os teoremas de {\Gamma}, podemos usar {\Gamma\vdash\alpha} para deduzir {\alpha}. Assim, acrescentamos a regra

\displaystyle \frac{\gamma_1,\dots,\gamma_k}{\alpha}

à nossa lista de regras de inferência.

Teorema 24 (Dupla negação (DN2)) {\vdash \alpha \rightarrow \neg\neg \alpha}

Prova:

1. {\neg\neg\neg \alpha \rightarrow \neg \alpha} (DN1)
2. {(\neg\neg\neg \alpha \rightarrow \alpha) \rightarrow ((\neg\neg\neg \alpha \rightarrow \neg\alpha)\rightarrow \neg\neg\neg\neg\alpha) } (A3)
3. {(\neg\neg\neg \alpha \rightarrow \neg\alpha) \rightarrow ((\neg\neg\neg \alpha \rightarrow \alpha)\rightarrow \neg\neg\neg\neg\alpha) } (TC)
4. {(\neg\neg\neg \alpha \rightarrow \alpha) \rightarrow \neg\neg\neg\neg\alpha} (MP 1,3)
5. {\neg\neg\neg \neg\alpha \rightarrow \neg\neg\alpha} (DN1)
6. {(\neg\neg\neg \alpha \rightarrow \alpha) \rightarrow \neg\neg\alpha} (SH 4,5)
7. {\alpha \rightarrow (\neg\neg\neg \alpha \rightarrow \alpha)} (A1)
8. {\alpha \rightarrow \neg\neg \alpha} (SH 7,6)

\Box

Teorema 25 (Generalização existencial (GE)) {\vdash [\alpha]_x^t \rightarrow \exists x\,\alpha}, se {t} é admissível para {x}.

Prova: Seja {t} uma substituição admissível para {x} em {\alpha}.

1. {\forall x\, \neg\alpha \rightarrow \neg[\alpha]_x^t } (A12)
2. {(\forall x\, \neg\alpha \rightarrow \neg[\alpha]_x^t) \rightarrow (\neg \neg[\alpha]_x^t \rightarrow \neg \forall x\, \neg\alpha) } (CP1)
3. { \neg \neg[\alpha]_x^t \rightarrow \neg \forall x\, \neg\alpha} (MP 1,2)
4. { [\alpha]_x^t \rightarrow \neg \neg[\alpha]_x^t } (DN2)
5. { [\alpha]_x^t \rightarrow \neg \forall x\, \neg\alpha} (SH 3,4)
6. { [\alpha]_x^t \rightarrow \exists x\, \alpha} (def. de {\exists})

\Box

Teorema 26 (Contra-positiva (CP2)) { \neg\beta \rightarrow \neg\alpha \vdash \alpha\rightarrow\beta}

Prova:

1. {\neg\beta\rightarrow\neg\alpha} (hip.)
2. {(\neg\beta\rightarrow\neg\alpha)\rightarrow(\neg\neg\alpha\rightarrow\neg\neg\beta)} (CP1)
3. {\neg\neg\alpha\rightarrow\neg\neg\beta} (MP 1,2)
4. {\alpha\rightarrow\neg\neg\alpha} (DN2)
5. {\neg\neg\beta\rightarrow\beta} (DN1)
6. {\alpha\rightarrow\neg\neg\beta} (SH 4,3)
7. {\alpha\rightarrow\beta} (SH 6,5)

\Box

Teorema 27 {\vdash \forall x\,\alpha\rightarrow \exists x\,\alpha}

Prova:

1. {\forall x\, \alpha \rightarrow [\alpha]_x^t } (AQ)
2. {[\alpha]_x^t \rightarrow \exists x\,\alpha} (GE)
3. {\forall x\,\alpha\rightarrow \exists x\,\alpha} (SH 1,2)

\Box

Com a notação usual temos:

  • (RA) {\displaystyle\frac{\alpha\rightarrow\beta,\alpha\rightarrow\neg\beta}{ \neg\alpha}}
  • (IC) {\displaystyle\frac{\alpha, \beta}{\alpha \land \beta}}
  • (EC1) {\displaystyle\frac{\alpha \land\beta}{\alpha} }
  • (EC2) {\displaystyle \frac{\alpha \land\beta}{\beta} }
  • (ID1) {\displaystyle \frac{\alpha}{\alpha \lor \beta}}
  • (ID2) {\displaystyle \frac{\beta}{\alpha \lor \beta}}
  • (DS) {\displaystyle \frac{\alpha, \neg\alpha}{\beta}}
  • (IU) {\displaystyle \frac{ \forall x\, \alpha}{ [\alpha]_x^t}}, para todo {t} admissível para {x}.
  • (Gen) {\displaystyle \frac{ \alpha}{ \forall x\, \alpha}}, se {x\not\in VL(\alpha)}.
  • (MT) {\displaystyle \frac{ \alpha\rightarrow\beta ,\neg\beta}{\neg\alpha}}
  • (CP1) { \displaystyle \frac{ \alpha\rightarrow\beta}{\neg\beta \rightarrow \neg\alpha}}
  • (SH) {\displaystyle \frac{ \alpha \rightarrow \beta, \beta \rightarrow \gamma }{\alpha \rightarrow \gamma}}
  • (TC) {\displaystyle \frac{\theta \rightarrow(\phi \rightarrow \xi)}{ \phi \rightarrow(\theta\rightarrow\xi)}}
  • (DN1) {\displaystyle \frac{\neg\neg\alpha}{ \alpha}}
  • (GE) {\displaystyle \frac{ [\alpha]_x^t}{ \exists\, \alpha}}, se {t} é admissível para {x}.
  • (CP2) { \displaystyle \frac{\neg\beta \rightarrow \neg\alpha}{ \alpha\rightarrow\beta}}
  • (DN2) {\displaystyle \frac{\alpha}{\neg\neg \alpha}}

  • ({\forall/\exists}) {\displaystyle \frac{\forall x\, \alpha}{\exists x\, \alpha}}

Teorema 28 {\forall x(\alpha\rightarrow\beta)\vdash (\alpha \rightarrow \forall x\beta)}, se {x\not\in VL(\alpha)}.

Prova:

1. {\forall x(\alpha\rightarrow\beta)} (hip.)
2. {\forall x(\alpha\rightarrow\beta)\rightarrow (\forall x\alpha \rightarrow \forall x\beta)} (A11)
3. {\forall x\alpha \rightarrow \forall x\beta} (MP 1,2)
4. {\alpha \rightarrow \forall x\beta} (SD 3,4)

\Box

O Teorema da Dedução

Na linguagem {\mathcal L_N} temos

1. {x=S0} (hip.)
2. {\forall x (x=S0)} (G)

donde concluímos {\vdash (x=S0)\rightarrow \forall x (x=S0)}, o que, intuitivamente, não deveria ser verdade.

Metateorema 48 Teorema da Dedução: Seja {\Gamma} subconjunto de fórmulas de uma linguagem de primeira ordem. Se { \Gamma\vdash \alpha\rightarrow\beta} então {\Gamma, \alpha \vdash \beta}. Se {\Gamma, \alpha \vdash \beta} e na dedução não foi usada a regra (G) com uma variável livre de {\alpha} então {\Gamma\vdash \alpha\rightarrow\beta}.

Em particular, {\Gamma\vdash \alpha\rightarrow\beta} se e só se {\Gamma, \alpha \vdash \beta} sempre que {\alpha} for uma sentença.

Prova: Primeiro, vamos demonstrar que

se {\Gamma \vdash \alpha\rightarrow\beta} então {\Gamma,\alpha \vdash \beta}.

Suponha que {\Gamma\vdash \alpha\rightarrow\beta}. Então

\displaystyle \Gamma,\alpha \vdash \alpha\rightarrow\beta

pela propriedade 2 de {\vdash}. Trivialmente, vale

\displaystyle \Gamma,\alpha \vdash \alpha.

Agora, pela regra do destacamento temos {\Gamma,\alpha \vdash \beta}. Agora, vamos demonstrar que

se {\Gamma,\alpha \vdash \beta} e (G) que torna uma variável livre de {\alpha} em ligada não ocorre nessa dedução então {\Gamma\vdash \alpha\rightarrow\beta}.

Suponha que {\Gamma,\alpha \vdash \beta} e seja

\displaystyle \langle\theta_1,\theta_2,\dots,\theta_{n-1},\beta\rangle

uma prova de {\beta} a partir de {\Gamma,\alpha}. Vamos demonstrar por indução em {i} que {\Gamma\vdash \alpha \rightarrow \theta_i} para todo {1\leq i\leq n} com {\theta_n=\beta}. Base: {\theta_1} ou é um axioma ou uma fórmula de {\Gamma\cup\{\alpha\}}. Se é axioma ou fórmula de {\Gamma} então

1. {\theta_1} (axioma ou hipótese)
2. {\theta_1 \rightarrow (\alpha \rightarrow \theta_1)} (A1)
3. {\alpha \rightarrow \theta_1} (MP 1,2)

e notemos que se {\theta_1} for {\alpha} então {\Gamma \vdash \alpha\rightarrow\alpha} por (A0). Portanto, em todos os casos {\Gamma \vdash \alpha \rightarrow \theta_1}.

Hipótese indutiva: Assuma que {\Gamma \vdash \alpha \rightarrow \theta_j} para todo {j=1,2,\dots,i-1}.

Passo indutivo: Vamos demonstrar que sob a hipótese indutiva, vale que {\Gamma \vdash \alpha \rightarrow \theta_i}.

A fórmula {\theta_i} ou é uma axioma ou fórmula de {\Gamma}, ou é {\alpha}, ou é resultado de uma regra de inferência: (MP j,k) ou (G j) com {j,k<i}. Nos três primeiros casos {\Gamma\vdash \alpha \rightarrow\theta_i}, a prova é similar ao caso feito na base da indução. Resta verificar o caso {\theta_i} é obtida por regra de inferência.

Se {\theta_i} é resultado de (MP j,k) com {j,k<i} então na linha j temos {\theta_j} e na linha k temos {\theta_j\rightarrow\theta_i}. Pela hipótese indutiva {\Gamma\vdash \alpha \rightarrow\theta_j} e {\Gamma\vdash \alpha \rightarrow (\theta_j\rightarrow\theta_i) }

1. {\alpha \rightarrow\theta_j} (hipótese)
2. {\alpha \rightarrow (\theta_j\rightarrow\theta_i)} (hipótese)
3. {(\alpha\rightarrow(\theta_j\rightarrow\theta_i))\rightarrow((\alpha\rightarrow\theta_j)\rightarrow(\alpha\rightarrow\theta_i) )} (A2)
4. {(\alpha\rightarrow\theta_j)\rightarrow(\alpha\rightarrow\theta_i)} (MP 2,3)
5. {\alpha\rightarrow\theta_i} (MP 1,4)

Agora, se {\theta_i} é resultado de (G j) com {j<i} então na linha j temos {\theta_j} e na linha i temos {\forall x\theta_j} com {x\not\in VL(\alpha)}. Pela hipótese indutiva {\Gamma\vdash \alpha \rightarrow\theta_j}

1. {\alpha \rightarrow\theta_j} (hipótese)
2. {\forall x\, (\alpha \rightarrow \theta_j )} (G)
3. {\forall x\, (\alpha \rightarrow \theta_j ) \rightarrow (\forall x\alpha \rightarrow \forall x\theta_j) } (A11)
4. {\forall x\alpha \rightarrow \forall x\theta_j } (MP 2,3)
5. {\alpha \rightarrow \forall x\alpha } (A13)
6. {\alpha \rightarrow \forall x\theta_j } (SH 4,5)

Portanto, pelo princípio da indução matemática {\Gamma\vdash \alpha\rightarrow\theta_i}, para todo {i}, ou seja {\Gamma\vdash \alpha\rightarrow\beta}. \Box

Há axiomas redundantes

Observamos aqui que os axiomas que estabelecemos para o sistema dedutivo não é o menor conjunto possível, dentre eles há várias redundâncias. Por exemplo, podemos retirar o axioma (A0) e provar

\displaystyle \vdash \alpha \rightarrow \alpha \ \ \ \ \ (6)

e com respeito a igualdade, também podemos provar a propriedade simétrica (A2I) usando os outros axiomas

\displaystyle \vdash (x = y) \rightarrow (y = x) \ \ \ \ \ (7)

As provas são dadas a seguir.

Prova:

1. {(\alpha \rightarrow((\alpha\rightarrow\alpha)\rightarrow \alpha)) \rightarrow ((\alpha\rightarrow(\alpha\rightarrow\alpha))\rightarrow(\alpha\rightarrow\alpha))} (A2)
2. {\alpha \rightarrow((\alpha\rightarrow\alpha)\rightarrow \alpha))} (A1)
3. {\alpha \rightarrow(\alpha \rightarrow \alpha))} (A1)
4. {(\alpha \rightarrow(\alpha \rightarrow \alpha))\rightarrow(\alpha\rightarrow\alpha)} (MP 2,1)
5 {\alpha \rightarrow \alpha} (MP 3,4)

\Box

Vejamos que {x=y \vdash y = x}. Prova:

1. {x = y} (hipótese)
2. {(x = y \land x = x) \rightarrow (x = x \rightarrow y = x) } (A3I)
3. {(x = y \land x = x) \rightarrow (x = x)} (A6)
4. {((x = y \land x = x) \rightarrow (x = x \rightarrow y = x) ) \rightarrow ( ((x = y \land x = x) \rightarrow (x = x)) \rightarrow ((x = y \land x = x) \rightarrow y = x))} (A2)
5. { ((x = y \land x = x) \rightarrow (x = x)) \rightarrow ((x = y \land x = x) \rightarrow y = x)} (MP 3,4)
6. {(x = y \land x = x) \rightarrow y = x)} (MP 4,5)
7. {x=x} (A1I)
8. {x = x \rightarrow (x = y \rightarrow (x = y \land x = x))} (A4)
9. {x = y \rightarrow (x = y \land x = x)} (MP 7,8)
10. {x = y \land x = x} (MP 1,9)
11. {y = x} (MP 1,10)

\Box

Existem várias axiomatizações da lógica de predicados, uma vez que, para qualquer lógica, há liberdade na escolha de axiomas e regras de inferência que caracterizam essa lógica. Descrevemos aqui um sistema Hilbert com 18 axiomas e duas regras de inferência. Poderímos ter restringido os 10 primeiros axiomas a

  1. {{\displaystyle \phi \rightarrow \left(\psi \rightarrow \phi \right)}}
  2. {{\displaystyle \left(\phi \rightarrow \left(\psi \rightarrow \xi \right) \right) \rightarrow \left(\left(\phi \rightarrow \psi \right) \rightarrow \left(\phi \rightarrow \xi \right) \right)}}
  3. {{\displaystyle \left(\lnot \phi \rightarrow \lnot \psi \right) \rightarrow \left(\psi \rightarrow \phi \right)}}

Esses axiomas descrevem a lógica proposicional clássica. Para manipular quantificadores universais basta

  1. {{\displaystyle \forall x \phi \rightarrow [\phi]^t_x}} onde {t} é admissível para {x} em {\phi}

dos três esquemas de axioma lógico que usamos (aqui em outra ordem)

  • {{\displaystyle \forall x \phi \rightarrow [\phi]^t_x}} onde {t} é admissível para {x} em {\phi}
  • {{\displaystyle \forall x \left(\phi \rightarrow \psi \right) \rightarrow \left(\forall x \phi \rightarrow \forall x \psi\right) }}
  • {{\displaystyle \phi \rightarrow \forall x \phi }} onde {x} não é uma variável livre de {\phi}.

os dois últimos são redundante em função da regra (G) de inferência. Com esses três axiomas podemos adotar somente modus ponens como regra de inferência. Notemos que, nesse caso o Teorema da Dedução vale plenamente, sem hipóteses adicionais. Ademais, podemos acrescentar

Metateorema 49 Teorema da Generalização: Seja {\Gamma} tal que a variável {x} não ocorre livre em nenhuma fórmula de {\Gamma}. Se {\Gamma\vdash \alpha} então {\Gamma\vdash \forall x\,\alpha}.

Dos esquemas de axioma para a igualdade, basta

  1. {{\displaystyle x = x}} para cada variável {x}
  2. {{\displaystyle \left(x = y \right) \rightarrow \left( [\phi]_z^x \rightarrow [\phi]_z^y \right)}}

Como os sistemas dedutivos do estilo de Hilbert têm poucas regras de dedução, é comum provar metateoremas que mostram que as regras de dedução adicionais não adicionam nenhum poder dedutivo, no sentido de que uma dedução usando as novas regras de dedução pode ser convertida em uma dedução usando apenas a dedução com as regras originais. Acima vimos várias delas as quais acrescentamos o teorema da generalização.

7.4. Axiomas não-lógicos e uma dedução na Aritmética

À linguagem {\mathcal L_N} acrescentamos, além dos axiomas lógicos, os seguintes axiomas não-lógicos específicos da teoria elementar de números:

  • (PA0) {\neg \exists x\, (Sx = 0)}
  • (PA1) {\forall x\forall y(Sx = Sy \rightarrow x = y)}
  • (PA2) {\forall x\, (x + 0 = x)}
  • (PA3) {\forall x\forall y\,(x + Sy = S(x + y))}
  • (PA4) {\forall x\,(x \cdot 0 = 0)}
  • (PA5) {\forall x\forall y\, (x \cdot Sy = (x \cdot y) + x)}
  • (PA6) Se {\varphi\in\mathcal L_N} com {x\in VL (\varphi)}, então

    \displaystyle \Big([\varphi]_x^0 \land \forall x \,\left(\varphi \rightarrow [\varphi]_x^{Sx}\right) \Big) \rightarrow \forall x\,\varphi

Notemos que PA0 — PA5 são axiomas, i.e. fórmulas da linguagem, enquanto que PA6 é um esquema de axioma, é o esquema de axioma da indução. Além desses, os axiomas de ordem

  • (OA0) {\neg(x<0)}
  • (OA1) {x< Sy \leftrightarrow x<y \lor x=y}
  • (OA2) { x<y \lor x=y \lor y<x} .

Na linguagem aritmética, por exemplo, teríamos o axioma lógico

\displaystyle ( x<y ) \rightarrow (\exists y\,(y = 0) \lor (x < y))

do esquema {\beta \rightarrow (\alpha \lor \beta)}. Agora, vamos provar que a soma é comutativa

\displaystyle \mathrm{PA} \vdash \forall x\forall y\, (x+y = y+x).

A prova é por indução em {x} com {\varphi} sendo a fórmula {\forall y\, (x+y = y+x)}.

A estratégia da prova é dividida em cinco passos. O primeiro é verificar a base da indução. O caso base consiste em deduzir a fórmula {[\varphi]^0_x}, ou seja, {\forall y\, (0+y = y+0)}, a qual é provada por indução em {y}. O segundo passo, o passo indutivo, consiste em provar {\forall x \,\left(\varphi \rightarrow [\varphi]_x^{Sx}\right)} que, no presente caso é a fórmula {\forall x \,\left((\forall y\, (x+y = y+x)) \rightarrow (\forall y\, (Sx+y = y+Sx)\right)}. O restante segue da seguinte maneira:

C1. {\forall y\, (0+y = y+0)} (base)
C2. {\forall x \,\left((\forall y\, (x+y = y+x)) \rightarrow (\forall y\, (Sx+y = y+Sx)\right)} (passo)
C3. {\forall y\, (0+y = y+0) \land \forall x \,\left((\forall y\, (x+y = y+x)) \rightarrow (\forall y\, (Sx+y = y+Sx)\right)} (IC)
C4. {\big(\forall y\, (0+y = y+0) \land \forall x \,\left((\forall y\, (x+y = y+x)) \rightarrow (\forall y\, (Sx+y = y+Sx)\right)\big) \rightarrow \forall x(\forall y\, (x+y = y+x)) } (PA6)
C5. {\forall x(\forall y\, (x+y = y+x)) } (MP C3,C4)

Para provar C1, começamos com

\displaystyle \mathrm{PA} \vdash \forall y\, (0+y = y). \ \ \ \ \ (8)

cuja prova será feita por indução em {y}. Isso é suficiente pois de {0+y=0} e {y+0=0} temos {0+y = y+0}, ou seja, {\mathrm{PA}\vdash \forall y\, (0+y=y+0)} (Exercício: escreva a prova formal).

A base da indução consiste em provar {0+0=0} e a passo indutivo consiste em provar {\forall y\, (0+y = y \rightarrow 0+Sy = Sy)}. A conclusão é como na estratégia acima:

B1. {0+0 = 0} (base)
B2. {\forall y\, (0+y = y \rightarrow 0+Sy = Sy)} (passo)
B3. {(0+0 = 0) \land \forall y\, (0+y = y \rightarrow 0+Sy = Sy)} (IC)
B4. {\big( (0+0 = 0) \land \forall y\, (0+y = y \rightarrow 0+Sy = Sy)\big) \rightarrow \forall y\, (x+y = y+x) } (PA6)
B5. {\forall y\, (0+y = y) } (MP B3,B4)

A seguir, detalhamos os passos B1 — B5 da sequência acima. A prova formal de (8) é

Prova:

1. {\forall x(x+0=0)} (PA2)
2. {\forall x(x+0=0) \rightarrow 0+0=0} (A1I)
3. {0+0=0} (MP 1,2)
4. {\forall x\forall y (x+Sy = S(x+y))} (PA3)
5. {\forall x\forall y (x+Sy= S(x+y)) \rightarrow \forall y (0+Sy= S(0+y) )} (A1I)
6. {\forall y (0+Sy= S(0+y) )} (MP 4,5)
7. {\forall y (0+Sy= S(0+y) ) \rightarrow 0+Sy= S(0+y)} (A1I)
8. {0+Sy= S(0+y)} (MP 6,7)
9. {0+y= y \rightarrow S(0+y) = Sy } (A5I)
10. {0+y= y \rightarrow (0+Sy= S(0+y)\land S(0+y) = Sy ) } (* 8,9)
11. {(0+Sy= S(0+y)\land S(0+y) = Sy ) \rightarrow (0+Sy= Sy )} (A16)
12. {0+y= y \rightarrow 0+Sy= Sy } (SH 10,11)
13. {\forall y\, (0+y= y \rightarrow 0+Sy = Sy )} (G 12)
12. {(0+0=0) \land (\forall y (0+Sy= S(0+y) ))} (IC 1,13)
13. { (0+0=0 \land \forall y\, ((0+y=0) \rightarrow (0+Sy=0))) \rightarrow \forall y (0+y=y) } (PA6)
14. {\forall y (0+y=0) } (MP 12,13)

\Box

\displaystyle \ \ \ \ \ (*) \ \ \ \ \ \beta, \, \alpha\rightarrow \gamma \vdash \alpha \rightarrow (\beta \land \gamma)

Prova:

1. {\beta} (hip.)
2. {\alpha\rightarrow \gamma} (hip.)
3. {\alpha} (hip.)
4. {\gamma} (MP 2,3)
5. {\beta \land \gamma} (IC 1,5)

\Box

Com isso temos {[\varphi]_x^0} ou seja {[ \forall y\, (x+y = y+x)]^0_x}. Agora, se provamos {\forall x \,\left(\varphi \rightarrow [\varphi]_x^{Sx}\right)}, ou seja, {\forall x \,\left((\forall y\, (x+y = y+x)) \rightarrow (\forall y\, (Sx+y = y+Sx)\right)} , temos a propriedade comutativa.

Exercício: {\forall x \,\left(\varphi \rightarrow [\varphi]_x^{Sx}\right)}, ou seja, {\forall x \,\left((\forall y\, (x+y = y+x)) \rightarrow (\forall y\, (Sx+y = y+Sx)\right)}.

Exercício:{ \mathrm{PA} \vdash \forall x ( x=0 \lor \exists y (x=Sy))}.

Deixe um comentário