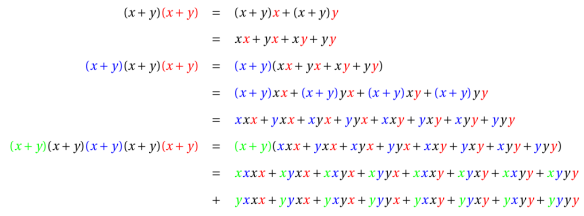bc0406 – Princípios da Análise Combinatória

Em probabilidade muitas vezes é importante contar de quantas maneiras diferentes um determinado evento pode ocorrer, por exemplo, num lançamento de dado um número par pode ocorrer de 3 modos, com o 2, o 4 e o 6. A seguir, descrevemos brevemente dois princípios básicos de contagem.

(1) Princípio Aditivo Suponha que nós queremos comprar um computador de um dos dois fabricantes mais comuns de processadores: Intel e AMD. Suponha também que nosso orçamento nos faz ter 12 opções de modelos Intel e 18 opções de modelos AMD. Então, existem no total ${12 + 18 = 30}$ opções diferentes de modelos de computador que podemos comprar.

Princípio Aditivo: Suponha que o evento ${E}$ pode ocorrer ${n}$ maneiras (ou que há ${n}$ desfechos possíveis para o evento ${E}$ ) e o evento distinto ${F}$ de ${m}$ maneiras (ou que há ${m}$ desfechos possíveis para o evento ${F}$ ). Então, o número de maneiras de ocorrer o evento “ ${E}$ ou ${F}$ ”, (ou, o número de possíveis desfechos para a ocorrência de um do eventos) é ${n+m}$ .

Em termos de conjuntos, o princípio aditivo é formulado da seguinte maneira

se ${T_1}$ e ${T_2}$ são conjuntos finitos disjuntos então ${|T_1\cup T_2|= |T_1|+|T_2|}$ .

De modo geral, se ${T_1}$ , ${T_2}$ , …, ${T_k}$ são conjuntos finitos disjuntos dois-a-dois então

$\displaystyle \left| \bigcup_{i=1}^k T_i \right| = \sum_{i=1}^k \big| T_i \big| .$

Exercício 1 Quantos inteiros entre ${1}$ e ${16}$ são múltiplos de ${3}$ ou de ${7}$ ?

Esboço da solução: ${E=\{3,6,9,12,15\}}$ e ${F=\{7,14\}}$ . ${E\text{ ou }F=\{3,6,7,9,12,14,15\}}$ . $\Box$

Exercício 2 Prove que se ${T_1}$ e ${T_2}$ são conjuntos finitos (não necessariamente disjuntos) então

$\displaystyle |T_1\cup T_2|= |T_1|+|T_2| -|T_1\cap T_2|.$

Exercício 3 Quantos inteiros entre ${1}$ e ${16}$ são múltiplos de ${3}$ ou de ${5}$ ?

Esboço da solução: ${E=\{3,6,9,12,15\}}$ e ${F=\{5,10,15\}}$ . ${E\text{ ou }F=\{3,6,7,9,12,14,15\}}$ . $\Box$

Exercício 4 Uma carta é escolhida de um maço de cartas de um baralho tradicional. De quantas maneiras podem ocorrer cada um dos eventos

escolher um rei ou uma rainha;
escolher uma carta de copa, ou de ouro, ou de pau;
escolher um número par ou uma espada;
escolher um rei ou uma carta preta.

(2) Princípio Multiplicativo Digamos que as únicas roupas limpas que você tem são duas camisetas e quatro calças. Quantos pares diferentes de camiseta e calça você pode escolher? São duas camisetas e pra cada escolha de camiseta é possível escolher uma de quatro calças, portanto, são ${2 \times 4 = 8}$ pares possíveis.

Princípio Multiplicativo: Se um evento é composto de duas etapas (ou eventos), a etapa ${1}$ pode ser realizada de ${n}$ maneiras distintas (ou que há ${n}$ desfechos possíveis para o evento ${1}$ ) e a etapa ${2}$ de ${m}$ maneiras (ou que há ${m}$ desfechos possíveis para o evento ${2}$ ), então o número de maneiras distintas de realizar o evento composto pelas duas etapas em sequência (ou, o número de possíveis desfechos para o evento 1 seguido do evento 2) é ${n \cdot m}$ .

Em termos de conjuntos, se ${E_1}$ e ${E_2}$ são conjuntos que representam os resultados das etapas, então o evento composto é representado por ${E_1\times E_2}$

se ${E_1}$ e ${E_2}$ são conjuntos finitos então ${|E_1 \times E_2|= |E_1|\cdot |E_2|}$ .

De um modo geral, se ${E_1}$ , …, ${E_r}$ representam ${r}$ etapas de evento composto, então o números de modos distintos de realizar o evento é

$\displaystyle \left| \prod_{i=1}^r E_i \right| = |E_1|\cdot|E_2|\cdots|E_r|.$

Exercício 5 Quantos números distintos de celulares com DDD 11 podem haver, quando cada celular é identificado com um número de 8 dígitos?

Esboço da solução: ${E_i=\{0,1,2,3,4,5,6,7,8,9\}}$ para ${i=1,2,\dots,8}$ .

${\left|\prod_{i=1}^8 E_i \right| = 10 \cdot 10 \cdots 10 = 10^8}$ . $\Box$

Exercício 6 Uma placa de carro é uma sequência de 3 letras seguidas por 4 dígitos. Qual é a quantidade de placas distintas que podemos obter?

Esboço da solução: ${E_i=\{A,B,\dots,Z\}}$ para ${i=1,2,3}$ .

${E_i=\{0,1,2,3,4,5,6,7,8,9\}}$ para ${i=4,5,6,7}$ .

${\left|\prod_{i=1}^8 E_i \right| = 23 \cdot 23 \cdot 23 \cdot 10 \cdot 10 \cdot 10 \cdot 10 = 23^3 10^4=121.670.000}$ . $\Box$

Exercício 7 Use o princípio multiplicativo para mostrar que um conjunto de cardinalidade ${n}$ tem ${2^n}$ subconjuntos distintos.

Solução: Seja ${A}$ um conjunto de cardinalidade ${n}$ . Se ${n=0}$ então ${A=\emptyset}$ é o único subconjunto dele mesmo e ${2^0=1}$ . Se ${n>1}$ então existe uma bijeção ${f\colon \{1,2,\dots,n\}\rightarrow A}$ .

Observemos que ${A=\{f(1),f(2),f(3),\dots,f(n)\}}$ .

Seja ${B\subset A}$ um subconjunto qualquer e consideremos o evento ${E_i}$ dado pela “pertinência de ${f(i)}$ em ${B}$ ”, para cada ${i\in \{1,2,\dots,n\}}$ , o qual tem 2 possíveis desfechos distintos, ${f(i) \in B}$ ou ${f(i) \not\in B}$ . Uma sequência de ${n}$ desfechos define exatamente um subconjunto.

Portanto, ${\left|\prod_{i=1}^n E_i \right| = 2^n}$ é o número total de desfechos, ou seja, de subconjuntos de ${A}$ . $\Box$

Um modelo para problemas de contagem é considerar a distribuição de bolas em caixas. Consideramos os casos caixas distinguíveis ou não e bolas distinguíveis ou não. Por exemplo, há 8 modos de distribuir as bolas distinguíveis ${a,b,c}$ em duas caixas, esquerda e direita

${abc \| }$			${ ab\|c}$			${ a \| bc}$			${ \|abc}$
${ac \| b }$			${ bc\|a}$			${ b \| ac}$			${ c\|ab}$

Se as caixas fossem indistinguíveis então ${abc | }$ e ${ |abc}$ definem a mesma configuração, assim como ${ac | b}$ e ${b | ac}$ , como ${ ab|c}$ e ${ c|ab}$ e, finalmente, como ${bc|a}$ e ${a | bc}$ . Portanto, há 4 modos de distribuir as bolas distinguíveis ${a,b,c}$ em duas caixas indistinguíveis. Se as bolas são indistinguíveis e as caixas não

${***}$ |

${**}$ | ${*}$

${*}$ | ${**}$

| ${***}$

são 4 modos e se caixas e bolas são indistinguíveis são 2 modos (por quê?).

Exercício 8 De quantas maneiras distintas podemos distribuir 3 bolas distinguíveis, digamos que uma é azul, uma verde e a outra vermelha, em 4 caixas distinguíveis, digamos que numeradas de 1 a 4.

Esboço da solução: Para cada bola há 4 possíveis caixas, portanto temos um evento composto por uma sequência de 3 eventos em que cada um tem 4 possíveis resultados, portanto ${4^3}$ maneiras distintas para distribuir as bolas nas caixas. $\Box$

Exercício 9 (Distribuição de bolas em caixas) De quantas maneiras distintas podemos distribuir ${r}$ bolas distinguíveis em ${n}$ caixas distinguíveis?

Esboço da solução: ${n^r}$ (justifique). $\Box$

A seguir destacamos alguns casos particulares do Princípio Multiplicativo. Essencialmente, são dois tipos de listas: arranjos e combinações. Nos arranjos a ordem dos elementos importa e nas combinações a ordem não importa.

(2.1) Arranjo Quantas palavras de 3 letras distintas podem ser formadas com o alfabeto de 26 letras? .Pelo princípio multiplicativo são ${26\cdot 25\cdot 24}$ palavras.

Um arranjo simples de ${r}$ elementos tomados de um conjunto ${A}$ de ${n}$ elementos ( ${r\leq n}$ ) é uma sequência ${(a_1,a_2,\dots,a_r)}$ de elementos não repetidos de ${A}$ .

O número de arranjos simples de ${r}$ elementos tomados de um conjunto de ${n}$ elementos ( ${r\leq n}$ ) é

$(n)_r \stackrel{\text{\tiny def}}{=} n(n-1)(n-2) \cdots (n-r+1)$

Quando é permitido repetição dizemos arranjo com repetição, que é um caso particular do Princípio Multiplicativo com todos os conjuntos iguais. Por arranjo nos referimos a arranjo simples.

Alguns textos usam a notação ${A(n,r)}$ para ${(n)_r}$ .

Exercício 10 Quantos inteiros entre ${100}$ e ${1.000}$ possuem todos os dígitos distintos?

Exercício 11 (Distribuição de bolas em caixas) De quantas maneiras distintas podemos distribuir ${r}$ bolas distinguíveis em ${n}$ caixas distinguíveis ( ${r\leq n}$ ) de modo que cada caixa receba no máximo ${1}$ bola?

Solução: Para cada uma das ${r}$ bolas, escolhemos uma caixa dentre as disponíveis, a qual se torna indisponível a partir de então. Temos o evento composto pela sequência ${E_1,E_2,\dots E_r}$ de eventos com ${|E_i|= |E_{i-1}|-1}$ ( ${1<i \leq n}$ ) e ${E_1 =n}$ , portanto

$\displaystyle \left| \prod_{i=1}^r E_i \right|= (n)_r$

maneiras distintas de distribuir ${r}$ bolas distinguíveis em ${n}$ caixas distinguíveis de modo que cada caixa receba no máximo ${1}$ bola. $\Box$

O caso de arranjo simples com ${r=n}$ é uma Permutação. Quantas palavras com letras distintas podem ser formadas com as letras ${a}$ , ${b}$ e ${c}$ ? Pelo princípio multiplicativo são ${3\cdot 2\cdot 1=6}$ palavras.

Uma permutação de elementos de um conjuntos ${A}$ é uma sequência de elementos de ${A}$ . Em outras palavras, é um arranjo com ${r=n}$ .

O número de permutações dos elementos de um conjunto de ${n}$ elementos é

$n! \stackrel{\text{\tiny def}}{=} n(n-1)(n-2) \cdots 1.$

Convenção:

${0!\,=\,1}$ .

Notemos que

$\displaystyle (n)_r= \frac{n!}{(n-r)!}.$

Por exemplo, o número de permutações possíveis com as letras ${a}$ , ${b}$ , ${c}$ , ${d}$ e ${e}$ é ${5!=120}$ . O número de permutações possíveis com as letras ${a}$ , ${b}$ , ${c}$ , ${d}$ , ${e}$ e ${f}$ é ${6!=720}$ .

Exercício 12 Qual é o número de permutações distintas com as letras da palavra banana?

Esboço da solução: São ${6!}$ permutações de 6 símbolos, mas as ${3!}$ permutações das letras ${a}$ são indistinguíveis, assim como as ${2!}$ dos ${n}$ ‘s. Portanto

$\displaystyle \frac {6!}{ 3! 2 !} = 60.$

$\Box$

Exercício 13 Um sinal é composto por nove bandeiras alinhadas. Quantos sinais diferentes é possível formar quando há disponíveis 4 bandeiras brancas, três bandeiras vermelhas e duas bandeiras azuis? Bandeiras da mesma cor são idênticas.

Esboço da solução: ${\frac {9!}{4!3!2!}=1260}$ . $\Box$

No caso de permutação com repetição de objetos se são ${n}$ objetos no total, com ${r}$ tipos de objetos distintos, ${k_i}$ objetos do tipo ${i}$ ( ${1\leq i\leq r}$ , ${k_1+k_2+\cdots+k_r=n}$ ) temos ${n!}$ permutações donde descontamos as ${k_i!}$ permutações de objetos do mesmo tipo, resultando

$\binom {n}{k_1,~k_2,\dots,~k_r} \stackrel{\text{\tiny def}}{=} \frac{n!}{k_1! k_2! \cdots k_r!}$

chamado de coeficiente multinomial.

Exercício 14 (Distribuição de bolas em caixas) De quantas maneiras distintas podemos distribuir ${n}$ bolas distinguíveis em ${r}$ caixas distinguíveis de modo que a caixa 1 receba ${k_1}$ bolas, a caixa 2 receba ${k_2}$ bolas, e assim por diante até que a caixa ${r}$ receba ${k_r}$ bolas.

Solução: Para cada uma das ${n!}$ permutações das bolas, colocamos as ${k_1}$ primeiras da sequência na caixa 1, as ${k_2}$ próximas na caixa 2 e assim por diante. As ${k_1}$ primeiras podem ocorrer de ${k_1!}$ maneiras distintas e aqui ordem não importa pois vão todas para a mesma caixa independentemente da ordem, as ${k_2}$ próximas de ${k_2!}$ maneiras distintas, e assim por diante. Cada maneira de distribuir as bolas nas caixas de acordo com a restrição enunciada pode ser obtida por uma permutação como acima, portanto o número de maneiras é ${\binom {n}{k_1,~k_2,\dots,~k_r} }$ . $\Box$

(2.2) Combinações Tomemos um arranjo de ${r}$ elementos escolhidos de um conjunto com ${n}$ elementos. A quantidade de arranjos que têm os mesmos ${r}$ elementos é ${r!}$ pois a única diferença entre eles é a ordem com que se apresentam os ${r}$ elementos. Quando essa ordem não importa o que temos são combinações.

Uma combinação de ${r}$ elementos escolhidos de um conjunto ${A}$ com ${n}$ elementos é simplesmente um subconjunto com ${r}$ elementos de ${A}$ .

O número de combinações de ${r}$ elementos tomados de um conjunto de ${n}$ elementos é o coeficiente binomial

$\binom nr \stackrel{\text{\tiny def}}{=} \frac{(n)_r}{r!} = \frac{n!}{r!(n-r)!}.$

Exercício 15 Numa população com ${n}$ elementos, ${n_1}$ são azuis e ${n_2=n-n_1}$ são verdes. De quantas maneiras podemos escolher ${k}$ elementos com ${r}$ deles azuis? ${(0\leq r \leq \min\{n_1,k\})}$

Esboço da solução:

Número de maneiras de escolher ${k-r}$ verdes ${\binom {n_2}{k-r}}$ .

Número de maneiras de escolher ${r}$ azuis ${\binom {n_1}{r}}$ .

Pelo Princípio Multiplicativo ${\binom {n_2}{k-r}\binom {n_1}{r}}$ . $\Box$

Se ${A}$ é um conjunto com ${n}$ elementos então a quantidade de subconjuntos de ${A}$ de cardinalidade ${r}$ é ${\binom nr}$ , como há ${2^n}$ subconjuntos de ${A}$ concluímos que

$\displaystyle \sum_{r=0}^n \binom nr = 2^n \ \ \ \ \ (2)$

Esse fato é consequência, também, de um resultado mais geral conhecido como

Teorema Binomial: Para todo ${n>0}$ , vale $(x+y)^n = \sum_{r=0}^n \binom nr x^r y^{n-r}.$

Fazendo ${x=y=1}$ temos (2).

Vejamos como o produto de desenvolve para valores pequenos de ${n}$

Assim, ${(x+y)^n = }$

$\displaystyle (x+y)(x+y)\cdots (x+y) \ \ \ \ \ (3)$

${n}$ ocorrências de ${(x+y)}$ ; cada termo do produto é da forma ${x^r y^{n-r}}$ , para ${0\leq r \leq n}$ ; para cada ${r}$ nesse intervalo o coeficiente de ${x^r y^{n-r}}$ é o número de maneiras de escolher o ${x}$ dentre os ${r}$ fatores de (3) e o ${y}$ dentre os ${n-r}$ fatores restantes de (3). O número de maneiras de escolher ${r}$ objetos dentre ${n}$ é ${\binom nr}$ , portanto

$\displaystyle (x+y)^n = \sum_{r=0}^n \binom nr x^r y^{n-r}. \ \ \ \ \ (4)$

Exercício 16 (Distribuição de bolas em caixas) De quantas maneiras distintas podemos distribuir ${r}$ bolas idênticas em ${n}$ caixas distinguíveis ( ${r\leq n}$ ) de modo que cada caixa receba no máximo ${1}$ bola?

Solução: Das ${n}$ caixas podemos escolher ${r}$ de ${\binom nr}$ maneiras diferentes, como as bolas são indistinguíveis distribuímos arbitrariamente uma por caixa. $\Box$

Exercício 17 Quantos dominós há com os números de 0 a 7?

Esboço da solução: Os dominós com pares de números diferentes são ${\binom 82 = 28}$ , mais os ${8}$ pares repetidos resultam em ${36}$ dominós. $\Box$

O caso acima pode ser generalizado como segue. Dentre ${n}$ objetos, queremos selecionar ${r}$ podendo haver repetição. Isso pode ser feito de

$\displaystyle \binom{n+r-1}r \ \ \ \ \ (5)$

maneiras diferentes. No caso dos dominós

$\displaystyle \binom{8+2-1}2 = \binom 92 = \frac{9!}{7!2!}=36.$

Uma maneira de provar (5) é modelar o problema como um problema de distribuição de bolas em caixas. Uma seleção de ${r}$ objetos dentre ${n}$ podendo haver repetição equivale a distribuir ${r}$ bolas indistinguíveis em ${n}$ caixas distinguíveis. Uma caixa vazio corresponde a um objeto não selecionado, uma caixa com ${k}$ bolas corresponde a um mesmo objeto repetido ${k}$ vezes. Se denotamos por ${x_i}$ a quantidade de bolas na caixa ${i}$ , então o número de maneiras de distribuir as bolas é a quantidade de soluções da equação

$\displaystyle x_1+x_2+x_3+\cdots+x_n=r \ \ \ \ \ (6)$

$\displaystyle \text{sujeito a }x_i \in \{0,1,2,\dots\} \text{ para todo }i.$

Por exemplo, para distribuir ${5}$ bolas idênticas em ${7}$ caixas podemos podemos representar bolas por ${*}$ e caixas pelos separadores ${|}$ de modo que

$\displaystyle *| ~ |~ | ** | *|* |$

significa ${x_1=1}$ (1 bola na 1ª caixa), ${x_2=x_3=0}$ (2ª e 3ª caixas vazias) ${x_4=2}$ , ${x_5=x_6=1}$ e ${x_7=0}$ . A quantidade de tais padrões distintos é

$\displaystyle \binom{7+5-1}5.$

— Soluções inteiras de equações —

Vamos começar com um caso simples

$\displaystyle x_1+x_2+x_3=6 \ \ \ \ \ (7)$

$\displaystyle \text{sujeito a }x_i \in \{1,2,\dots\} \text{ para todo }i.$

Consideremos

$\displaystyle 1+1+1+1+1+1 = 6$

e uma solução de (7) corresponde a escolha de ${2}$ operadores ${+}$ dentre os ${5}$ escritos na equação acima; por exemplo, se usamos ${\oplus}$ par as escolhas

$\displaystyle \underbrace{1+1}_{x_1} \oplus \underbrace{1+1+1}_{x_2} \oplus \underbrace{1}_{x_3} = 5$

corresponde a ${x_1=2}$ , ${x_2=3}$ e ${x_3=1}$ , e

$\displaystyle \underbrace{1+1}_{x_1} \oplus \underbrace{1+1}_{x_2} \oplus \underbrace{1+1}_{x_3} = 5$

corresponde a ${x_1=2}$ , ${x_2=2}$ e ${x_3=2}$ .

No caso geral,

$\displaystyle x_1+x_2+x_3+\cdots+x_n=r \ \ \ \ \ (8)$

$\displaystyle \text{sujeito a }x_i \in \{1,2,\dots\} \text{ para todo }i.$

consideramos ${1+1+1+\cdots+1=r }$ e dos ${r-1}$ operadores ${+}$ escolhemos ${n-1}$ , ou seja, são

$\displaystyle \binom{r-1}{n-1} \ \ \ \ \ (9)$

soluções inteiras positivas.

Exercício 18 Mostre que a equação (6) tem

$\displaystyle \binom{n+r-1}r.$

soluções (observe que há uma diferença no domínio das soluções e que $\binom{n+r-1}r = \binom{n+r-1}{n-1}.$ ).

— Fórmula de Stirling —

Duas sequências de números ${a_n}$ e ${b_n}$ são assintoticamente iguais, e escrecemos ${a_n \sim b_n}$ , se

$\displaystyle \lim_{n\rightarrow\infty} \frac{a_n}{b_n}=1.$

Frequentemente, é muito útil quanto trabalhamos com fatoriais a seguinte igualdade assintótica conhecida como fórmula de Stirling

$\displaystyle n! \sim n^n \mathrm{e}^{-n}\sqrt{2\pi n}. \ \ \ \ \ (10)$

— Exercícios —

Prove que
$\displaystyle (x+y+z)^n = \sum_{\substack{k_1,~k_2,~k_3\in{\mathbb N}\\k_1+k_2+k_3=n}}\binom n{k_1,~k_2,~k_3} x^{k_1}y^{k_2}z^{k_3}.$
Prove que ${\binom nr = \binom n{n-r}}$ .
Prove por indução os casos gerais dos Princípios Aditivo e Multiplicativo.
Quantos subconjuntos formados por elementos do conjunto satisfazem a propriedade:
1. a diferença entre o menor elemento e o maior elemento é ${5}$ ,
2. a diferença entre o menor elemento e o maior elemento é menor que ${5}$ ,
3. a soma do menor elemento e o maior elemento é ímpar,
4. o maior é o dobro do menor,
5. o maior é divisível pelo menor.
De quantas maneiras podemos
1. distribuir ${r}$ bolas distintas em ${n}$ caixas distintas com qualquer número de bolas por caixa;
2. distribuir ${r}$ bolas distintas em ${n}$ caixas distintas com no máximo uma bola por caixa;
3. distribuir ${r}$ bolas idênticas em ${n}$ caixas distintas com no máximo uma bola por caixa;
4. distribuir ${r}$ bolas idênticas em ${n}$ caixas distintas com qualquer número de bolas por caixa.
Formule os seguintes problemas em termos de soluções inteiras de equações:
1. O número de maneiras de distribuir ${r}$ bolas idênticas em ${n}$ caixas distintas com pelo menos ${k}$ bolas na primeira caixa.
2. O número de maneiras de distribuir ${r}$ bolas idênticas em ${n}$ caixas distintas com nenhuma caixa com mais de duas bolas.
3. O número de subconjuntos de ${\{A,B,C,D,E\}}$ com ${3}$ elementos.
4. O número de maneiras de distribuir ${r}$ bolas idênticas em ${n}$ caixas distintas tal que as duas primeiras caixas tenham juntas ${p}$ bolas.
Formule os seguintes problemas em termos de soluções inteiras de equações e distribuição de bolas em caixas:
1. Seleção de seis sorvetes a partir de ${31}$ sabores
2. Seleção de cinco camisas de um grupo de cinco vermelhas, quatro azuis e duas amarelas.
3. Seleção de ${12}$ cervejas de ${4}$ tipos com pelo menos duas de cada tipo.
4. Seleção de ${20}$ refrigerantes de ${4}$ tipos com número par de cada tipo e não mais que oito do mesmo tipo.
De quantas maneiras podemos dispor ${8}$ peças brancas idênticas e ${8}$ peças pretas idênticas num tabuleiro de xadrez ( ${8\times 8}$ )? Quantas são simétricas (a disposição ficará a mesma quando rotacionamos o tabuleiro de 180 graus)?
De quantas maneiras pode ocorrer que num grupo com 25 pessoas 2 ou mais pessoas façam aniversário no mesmo dia.
Prove que o número de combinações de ${n}$ elementos tomados ${p}$ -a- ${p}$ com repetição é igual ao número de soluções inteira não-negativas da equação linear ${X_1+X_2+\cdots +X_n=p}$ exibindo uma bijeção ente os dois conjuntos.
Determine o número de soluções da equação nos casos
1. ${X_i\geq 0}$ ;
2. ${X_i>0}$ ; e
3. ${X_i>i}$ .
Uma caixa tem um número desconhecido de bolas idênticas, que denotamos por , e queremos estimá-lo. Para tal, selecionamos aleatoriamente bolas, cada uma recebe uma marca e é devolvida para a caixa.
1. De quantas maneiras podemos extrair ${r}$ bolas de modo que ${k}$ estarão marcadas?
2. Qual é o número de seleções de ${r}$ bolas.
3. Defina o índice de acerto por Mostre que é
  1. crescente para os valores de ${n}$ tais que ${p_k(n)>p_k(n-1)}$ ,
  2. decrescente para os valores de ${n}$ tais que ${p_k(n)<p_k(n-1)}$ .
Conclua que ${\lfloor {n_1r}/{k} \rfloor}$ é ponto de máximo de ${p_k(n)}$ .
Atribuindo um valor apropriado a na expansão binomial de ou em alguma de suas derivadas, mostre as identidades
1. $(x+y)^n= \sum_{k=0}^{n}\binom{n}{k}x^{n-k}b^k$ .
2. $\sum_{k=0}^{n}(-1)^kk\binom{n}{k}=0$ .
3. $\sum_{k=0}^{n}k(k-1)\binom{n}{k}=n(n-1)2^{n-2}$ .