bc0402 Integral

Seja ${f}$ uma função definida no intervalo ${[a,b]}$ , façamos ${x_0=a, ~x_n=b}$ e consideremos o intervalo ${[a,b]}$ dividido pelos pontos ${x_1 < x_2 < \cdots < x_{n-1}}$ em ${n}$ partes não necessariamente de mesmo comprimento. Em cada subintervalo escolhemos um ponto arbitrário ${\xi_i \in [x_{i-1},x_{i}]}$ ( ${0<i\leq n}$ ) e consideremos os retângulos de altura ${f(\xi_i)}$ e base ${\Delta x_i = x_{i}-x_{i-1}}$ .

A soma

$\displaystyle S_n = \sum_{i=1}^n f(\xi_i)\Delta x_i \ \ \ \ \ (31)$

é chamada Soma de Riemann relativa aos pontos ${x_i}$ e ${\xi_i}$ , ${0< i < n}$ . Geometricamente, essa soma corresponde a diferença entre a soma das áreas dos retângulos de altura ${f(\xi_i)\Delta x_i}$ que estão acima do eixo ${x}$ e a soma das áreas dos retângulos abaixo do eixo ${x}$ .

Queremos saber se quando o número de subintervalos aumenta indefinidamente e ao mesmo tempo o tamanho dos intervalos tende a zero, então o limite da sequência ${\lim_{n\rightarrow\infty}S_n}$ existe e de forma independente das escolhas dos pontos ${x_i}$ e ${\xi_i}$ . Para sermos mais precisos, escrevemos

$\displaystyle \lim_{\substack{n\to\infty\\\max\Delta x_i \rightarrow 0}} \left(\sum_{i=1}^n f(\xi_i)\Delta x_i\right) = S$

se para todo ${\varepsilon >0}$ existir ${\delta >0}$ tal que ${|S_n -S|< \varepsilon}$ sempre que ${\Delta x_i<\delta}$ para todo ${i}$ , independentemente da escolha dos ${x_i}$ e dos ${\xi_i}$ .

A integral definida da função ${f}$ no intervalo ${[a,b]}$ é

$\displaystyle \int_a^b f(x)\;\mathrm{d}x \stackrel{{\textrm{\tiny def}}}{=} \lim_{\substack{n\to\infty\\\max\Delta x_i \rightarrow 0}} \left(\sum_{i=1}^n f(\xi_i)\Delta x_i\right)$

e quando tal integral existe dizemos que ${f}$ é Riemann-integrável, ou simplesmente integrável em ${[a,b]}$ .

Na verdade, saber quando o limite ${S}$ existe, ou seja, determinar quais funções são integráveis, é um problema além dos objetivos dessa disciplina. Nós assumiremos o seguinte resultado sem demonstração.

Teorema 18 Se ${f}$ é contínua em ${[a,b]}$ então ${f}$ é integrável em ${[a,b]}$ . Se ${f}$ não é contínua em apenas um número finitos de pontos de ${[a,b]}$ mas é limitada em ${[a,b]}$ então ${f}$ é integrável em ${[a,b]}$ . ${\Box}$

Como consequência desse teorema, se ${f}$ for contínua então basta uma escolha conveniente de ${x_i}$ e ${\xi_i}$ e determinar o limite da soma de Riemann.

Exemplo 70 A integral definida de ${f(x) = k}$ , ${k}$ uma constante qualquer, no intervalo ${[a,b]}$ é dada, já que a função é contínua, pelo processo limite quando escolhemos ${x_0=a}$ e para ${1\leq i \leq n-1}$ tomamos ${x_i= x_{i-1}+ \frac {b-a}n}$ e ${x_n=b}$ , e em cada intervalo ${[x_{i-1},x_i]}$ tomamos ${\xi_i = x_i}$ e assim para cada ${n}$

$\displaystyle \sum_{i=1}^n f(\xi_i)\Delta x_i = \sum_{i=1}^n k \frac {b-a}n = k(b-a)$

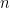
portanto, ${\int_a^b k\,\mathrm{d}x = (b-a)k}$ .

Exemplo 71 A integral definida de ${f(x) = x}$ no intervalo ${[a,b]}$ é dada, já que a função é contínua, pelo processo limite quando escolhemos ${x_0=a}$ e para ${1\leq i \leq n-1}$ tomamos ${x_i= x_{i-1}+ \frac {b-a}n}$ e ${x_n=b}$ , e em cada intervalo ${[x_{i-1},x_i]}$ tomamos ${\xi_i = x_i}$ e assim para cada ${n}$

$\displaystyle \sum_{i=1}^n f(\xi_i)\Delta x_i = \sum_{i=1}^n f(x_i) \frac {b-a}n = \sum_{i=1}^n x_i \frac {b-a}n .$

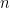
Não é difícil constatar que ${x_i = a+ i \frac{b-a}n}$ , logo

$\displaystyle \sum_{i=1}^n x_i = an + \frac{b-a}n \sum_{i=1}^n i = an + \frac{b-a}n \times \frac{n(n+1)}2$

portanto,

$\displaystyle \sum_{i=1}^n x_i \frac {b-a}n =(b-a)\left( a + \frac{b-a}n \times \frac{(n+1)}2 \right)$

cujo limite quando ${n\rightarrow \infty}$ é

$\displaystyle \int_a^b k\,\mathrm{d}x = \frac 12(b^2-a^2).$

Exemplo 72 Para ${f\colon [0,b] \rightarrow {\mathbb R}}$ dada por ${f(x)=x^2}$ dividimos o intervalo ${[0,b]}$ em ${n}$ subintervalos ${I_1=[0,h]}$ , ${I_2=[h,2h]}$ ,\dots, ${I_n=[(n-1)h,b]}$ , para ${h=b/n}$ . Em cada subintervalo ${I_j}$ fazemos ${\xi_j = jh}$ e temos

$\displaystyle S_n= \sum_{j=1}^n j^2h^2 = h^3 \sum_{j=1}^n j^2 = h^3\frac{n(n+1)(2n+1)}6$

pois ${\sum_j j = n(n+1)/2}$ e ${\sum_j j^2 = n(n+1)(2n+1)/6}$ , e como ${h=b/n}$ temos que

$\displaystyle S_n = \frac{b^3}{6} \frac{n(n+1)(2n+1)}{n^3}$

e

$\displaystyle \int_0^b x^2\,\mathrm{d}x = \lim_{n\rightarrow+\infty} S_n=\frac{b^3}3.$

Exemplo 73 Seja ${f}$ definida em ${{\mathbb R}}$ por ${f(x)=0}$ se ${x\neq 1,3,5}$ e ${f(1)=f(3)=f(5)=1}$ . Essa função é limitada e descontínua em três pontos do domínio.

Para determinar ${\int_0^2 f(x)\,\mathrm{d}x}$ usamos qualquer escolha de ${x_i}$ e ${\xi_i}$ . Quando calculamos ${\sum_{i=1}^n f(\xi_i)\Delta x_i}$ os termos são ${0}$ exceto se ocorrer ${\xi_j=1}$ para algum ${j}$ , onde a soma vale ${\Delta x_j}$ , logo no limite ${\int_0^3 f(x)\,\mathrm{d}x = 0}$ .

Para determinar ${\int_0^4 f(x)\,\mathrm{d}x}$ usamos qualquer escolha de ${x_i}$ e ${\xi_i}$ . Quando calculamos ${\sum_{i=1}^n f(\xi_i)\Delta x_i}$ os termos são ${0}$ exceto se ocorrer ${\xi_j=1}$ para algum ${j}$ , onde a soma vale ${\Delta x_j}$ , ou se ocorrer ${\xi_j=3}$ para algum ${j}$ onde a soma vale ${\Delta x_j}$ , ocorrer ${\xi_{j_1}=1}$ e ${x_{j_2}= 1}$ para algum ${j_1}$ e algum ${j_2}$ , onde a soma vale ${\Delta x_{j_1} + \Delta x_{j_2}}$ . Em todos os casos ${\int_0^3 f(x)\,\mathrm{d}x = 0}$ .

Para determinar ${\int_0^6 f(x)\,\mathrm{d}x}$ usamos qualquer escolha de ${x_i}$ e ${\xi_i}$ e podem ocorrer

$\displaystyle \sum_{i=1}^n f(\xi_i)\Delta = \begin{cases} 0 & \textrm{ se } \xi_i \neq 1,3,5\\ \Delta x_{j_1} + \Delta x_{j_2} & \textrm{ se } \xi_{j_1}=1,~\xi_{j_2}=3\\ \Delta x_{j_1} + \Delta x_{j_3} & \textrm{ se } \xi_{j_1}=1,~\xi_{j_3}=5\\ \Delta x_{j_2} + \Delta x_{j_3} & \textrm{ se } \xi_{j_2}=3,~\xi_{j_3}=5\\ \Delta x_{j_2} + \Delta x_{j_3} + \Delta x_{j_3} & \textrm{ se } \xi_{j_1}=1,~\xi_{j_2}=3,~\xi_{j_3}=5 \end{cases}$

em qualquer caso, no limite quando ${\max\Delta x_i\rightarrow 0}$ os termos tendem a ${0}$ e no limite ${\int_0^6 f(x)\,\mathrm{d}x = 0}$ .

O caso acima exemplifica um fenômeno mais geral: a valor de ${\int_a^b f(x)\,\mathrm{d}x}$ não muda se alterarmos o valor da função ${f}$ num conjunto finito de pontos do intervalo. Além desse fato, vimos um exemplo de que uma função pode não ser contínua e ainda sim ser integrável.

Observação 4 ${ \int_a^b f(x)\,\mathrm{d}x}$ , ${ \int_a^b f(t)\,\mathrm{d}t}$ , e ${ \int_a^b f(u)\,\mathrm{d}u}$ têm o mesmo significado, ou seja, o símbolo que usamos para a variável independente é indiferente.

A integral definida satisfaz as seguintes propriedades, dado que as integrais existem. Para ${a<c<b}$ e para qualquer ${k\in{\mathbb R}}$

$\displaystyle \int_a^a f(x)\;\mathrm{d}x = 0$

$\displaystyle \int_b^a f(x)\;\mathrm{d}x = - \int_a^b f(x)\;\mathrm{d}x$

$\displaystyle \int_a^b kf(x)\;\mathrm{d}x = k\int_a^b f(x)\;\mathrm{d}x$

$\displaystyle \int_a^b \big(f(x)+g(x)\big)\;\mathrm{d}x = \int_a^b f(x)\;\mathrm{d}x+\int_a^b g(x)\;\mathrm{d}x$

$\displaystyle f(x) \leq g(x) \Rightarrow \int_a^b f(x)\;\mathrm{d}x \leq \int_a^b g(x)\;\mathrm{d}x$

$\displaystyle \int_a^b f(x)\;\mathrm{d}x = \int_a^c f(x)\;\mathrm{d}x + \int_c^b f(x)\;\mathrm{d}x$

$\displaystyle \left| \int_a^b f(x)\;\mathrm{d}x\right| \leq \int_a^b \left| f(x) \right|\;\mathrm{d}x$

Funções não limitadas não possuem integral definida (reflita sobre isso). Notemos que ambas hipóteses do teorema 18 pedem função limitada, isso por que se ${f}$ é contínua em ${[a,b]}$ então existem ${m}$ e ${M}$ em ${[a,b]}$ tais que

$\displaystyle f(m) \leq f(x) \leq f(M)$

para todo ${x\in [a,b]}$ , pelo Teorema do valor extremo de Weierstrass. Ademais,

$\displaystyle \int_a^bf(m)\,\mathrm{d}x \leq \int_a^bf(x)\,\mathrm{d}x \leq \int_a^bf(M)\,\mathrm{d}x$

que pelo exemplo 70 resulta em

$\displaystyle (b-a) f(m) \leq \int_a^bf(x)\,\mathrm{d}x \leq (b-a)f(M)$

e como ${f}$ é contínua, para cada ${y\in [f(m),f(M)]}$ deve haver ${c\in [a,b]}$ tal que ${f(c)=y}$ , o que nos permite enunciar o seguinte teorema, tomando $y=\frac 1{b-a}\int_a^b f(x)\,\mathrm{d}x$ .

Teorema 19 (TVM do cálculo integral) Seja ${f}$ contínua em ${[a,b]}$ . Existe ${c\in [a,b]}$ tal que

$\displaystyle \int_a^b f(x)\;\mathrm{d}x = f(c)(b-a).$

Vale o seguinte resultado mais geral.

Exercício 95 (TVM do cálculo integral — forma geral) Sejam ${f}$ e ${g}$ contínuas em ${[a,b]}$ e ${g}$ positiva. Mostre que existe ${\xi\in [a,b]}$ tal que

$\displaystyle \int_a^bf(x)g(x)\;\mathrm{d}x =f(c)\int_a^b g(x)\;\mathrm{d}x.$

— Teoremas Fundamentais do Cálculo —

Dada uma função ${f}$ contínua no intervalo fechado ${I}$ e fixada uma constante ${a\in I}$ temos que

$\displaystyle \Phi_a(x) =\int_a^x f(u)\;\mathrm{d}u$

é uma função definida para todo ${x\in I}$ . A taxa de variação dessa função é

$\displaystyle \frac{\Phi_a(x+h)-\Phi_a(x)}h = \frac 1h \int_a^{x+h}f(u)\;\mathrm{d}u- \frac 1h \int_a^{x}f(u)\;\mathrm{d}u = \frac 1h \int_x^{x+h}f(u)\;\mathrm{d}u$

e do teorema 19 existe ${c\in [x,x+h]}$ tal que

$\displaystyle f(c) = \frac 1h \int_x^{x+h}f(u)\;\mathrm{d}u$

e fazendo ${h\rightarrow 0}$ obtemos ${f(c)\rightarrow f(x)}$ , isto é

$\displaystyle \Phi_a'(x) = \lim_{h\rightarrow 0} \frac {\Phi_a(x+h)-\Phi_a(x)}h = f(x)$

espetacularmente, a derivada de ${\Phi_a}$ é ${f}$ , ou seja ${\Phi_a}$ é uma primitiva de ${f}$ .

Seguindo alguns autores, chamamos ${\int_a^x f(u)\;\mathrm{d}u}$ uma integral indefinida de ${f}$ e o fato deduzido acima de Teorema Fundamental do Cálculo.

Teorema 20 (Primeiro Teorema Fundamental do Cálculo (TFC)) Sejam ${f}$ contínua em ${I}$ e ${a\in I}$ fixo, então ${\Phi_a\colon I\rightarrow {\mathbb R}}$ dada por

$\displaystyle \Phi_a(x) = \int_a^x f(u)\;\mathrm{d}u$

é derivável em ${(a,b)\subset I}$ e ${\Phi'(x) = f(x)}$ para todo ${x\in (a,b)}$ . ${\Box}$

Observemos que se se mudamos o limitante inferior temos outra função primitiva cuja diferença para $\Phi_a$ é uma constante, como era de se esperar

$\displaystyle \Phi_c(x) -\Phi_a(x) =\int_c^x f(u)\;\mathrm{d}u - \int_a^x f(u)\;\mathrm{d}u= \int_a^c f(u)\;\mathrm{d}u$

${c\neq a}$ .

Exercício 96 Verifique que se definimos ${\Phi(x) = \int_x^b f(u)\,\mathrm{d}u}$ então ${\Phi ' (x) = -f(x)}$ .

Exercício 97 Seja ${F}$ uma primitiva de ${f}$ em ${I}$ . Mostre que ${F(x) = \Phi_a(x) + F(a)}$ .

Observação 5 No caso em que ${f(x)=0}$ temos ${\Phi_a(x) = 0}$ para qualquer ${a}$ , enquanto que ${k}$ (fixo) são as primitivas. No caso em que ${f(x)=\sqrt{x}}$ temos ${\Phi_a(x) = (2/3)x^{3/2} - (2/3)a^{3/2}}$ enquanto que ${(2/3)x^{3/2}+1}$ é uma primitiva que não é ${\Phi_a}$ para algum ${a}$ . Em resumo, se ${F}$ é uma primitiva de ${f}$ então ${F(x) = c + \Phi_a(x)}$ para ${a}$ e ${c}$ constantes e, reciprocamente, fixadas as constantes tal expressão define uma primitiva de ${f}$ .

Daqui em diante não faremos distinção entre integral indefinida e uma primitiva e também chamamos

$\displaystyle \int f(x)\;\mathrm{d}x = \int_a^xf(u)\,\mathrm{d}u + k$

de integral indefinida.

Como consequência disso tudo temos que se ${f}$ é contínua num intervalo então nesse intervalo ela tem primitiva. Ademais, suponha que ${F}$ seja uma primitiva e que desejamos saber ${\int_a^b f(x)\,\mathrm{d}x}$ . Sabemos que ${F(x) = \int_a^x f(u)\,\mathrm{d}u + F(a)}$ , portanto, fazendo ${x=b}$

$\displaystyle \int_a^b f(u)\,\mathrm{d}u = F(b)-F(a).$

Essa igualdade é tão útil que mereceria o nome de teorema fundamental do cálculo, mas como ele vale de uma forma mais geral da afirmação o segundo teorema fundamental é enunciado a seguir.

Teorema 21 (Segundo Teorema Fundamental do Cálculo (TFC)) Se ${f}$ é integrável em ${[a,b]}$ e ${F}$ é uma primitiva de ${f}$ em ${(a,b)}$ , então

$\displaystyle \boxed{\int_a^b f(u)\;\mathrm{d}u = F(b) -F(a)}.$

Demonstração: Se ${f}$ é integrável então existe o limite

$\displaystyle \lim_{\max\Delta x_i \rightarrow 0} \left(\sum_{i=1}^n f(\xi_i)\Delta x_i\right)$

para quaisquer escolhas de ${x_i}$ e ${\xi_i}$ ( ${1\leq i\leq n}$ ), em particular, pelo TVM existe ${\xi_i \in (x_{i-1},x_i)}$ tal que

$\displaystyle F(x_i)-F(x_{i-1}) = F'(\xi_i)(x_i-x_{i-1}) = f(\xi_i)(x_i-x_{i-1})$

portanto

$\displaystyle \sum_{i=1}^n [ F(x_i)-F(x_{i-1})] =\sum_{i=1}^n [ f(\xi_i)(x_i-x_{i-1}) ]$

que é equivalente a

$\displaystyle F(b)-F(a) = \sum_{i=1}^n f(\xi_i)\Delta x_i,$

em particular,

$\displaystyle F(b)-F(a) = \lim_{\Delta x_i \rightarrow 0} \sum_{i=1}^n f(\xi_i)\Delta x_i,$

portanto ${\int_a^b f(x)\,\mathrm{d}x = F(b)-F(a)}$ . $\Box$

A seguinte notação é muito usada

$\displaystyle \boxed{F(x) \Big|_a^b \stackrel{{\textrm{\tiny def}}}{=} F(b) -F(a)}.$

Observacao 6 Esse resultado não é a definição de integral definida, há funções integráveis que não são derivadas de qualquer função (por exemplo ${f(x)=0}$ se ${x\neq 1}$ e ${f(1)=1}$ ).

Exemplo 74 Fixados reais ${a<b}$ , sabemos que ${F(x) =x^3/3}$ é uma primitiva de ${f(x)=x^2}$ , portanto,

$\displaystyle \int_a^b x^2\;\mathrm{d}x = F(b) -F(a) = \frac{b^3}3 - \frac{a^3}3.$

Notemos que o resultado é o mesmo se usamos ${F(x) = x^3/3 + k}$ para qualquer constante ${k}$ .

Exercício 98 (Desigualdade de Cauchy—Schwarz) Sejam ${f}$ e ${g}$ contínuas em ${[a,b]}$ . Então

$\displaystyle \int_a^b|f(x)|^2\;\mathrm{d}x \int_a^b|g(x)|^2\;\mathrm{d}x \leq \left( \int_a^b f(x) g(x)\;\mathrm{d}x\right)^2.$

Exercício 99 Seja ${f}$ uma função ímpar e contínua em ${[-a,a]}$ ( ${a>0}$ ). Mostre que ${\int_{-a}^af(x)\,\mathrm{d}x =0}$ .

Exercício 100 (Mudança de variável) Sejam ${f}$ uma função contínua no intervalo ${I}$ e ${a,b\in I}$ . Suponha ${x=\varphi(t)}$ com ${\varphi}$ derivável em ${J}$ , ${\varphi(J)\subset I}$ e ${\varphi'}$ contínua em ${J}$ . Sejam ${\alpha,\beta\in J}$ tais que ${a=\varphi(\alpha)}$ e ${\beta=\varphi(b)}$ . Mostre que

$\displaystyle \int_a^b f(x)\;\mathrm{d}x = \int_\alpha^\beta f(\varphi(t))\varphi'(t)\;\mathrm{d}t$

— Integrais impróprias —

Até agora integramos funções limitadas com número finito de descontinuidades num intervalo fechado. Agora, estendemos a definição para intervalos infinitos e funções com descontinuidades infinitas no intervalo, por exemplo,

$\displaystyle \int_{-\infty}^{+\infty} \frac 1{1+x^2}\,\mathrm{d}x, ~\int_1^2 \frac 1{x-1}\,\mathrm{d}x, ~ \int_0^{+\infty} \frac 1{\sqrt x}\,\mathrm{d}x.$

A integral imprópria de ${f}$ no intervalo ${[a,+\infty)}$ é

$\displaystyle \int_a^{+\infty}f(x)\,\mathrm{d}x = \lim_{b\rightarrow +\infty}\int_a^bf(x)\,\mathrm{d}x$

quando o limite existe, caso contrário dizemos que a integral imprópria diverge.

Por exemplo,

$\displaystyle \int_1^{+\infty}\frac 1{x^3} \,\mathrm{d}x = \lim_{b\rightarrow +\infty} \left( \frac 12 - \frac 1{2b^2}\right) = \frac 12$

entretanto

$\displaystyle \int_1^{+\infty}\frac 1{x} \,\mathrm{d}x = \lim_{b\rightarrow +\infty} \log (b) = +\infty$

portanto é uma integral imprópria divergente.

Analogamente, a integral imprópria de ${f}$ no intervalo ${(-\infty,b]}$ é

$\displaystyle \int_{-\infty}^bf(x)\,\mathrm{d}x = \lim_{a\rightarrow -\infty}\int_a^bf(x)\,\mathrm{d}x$

quando o limite existe, caso contrário dizemos que a integral imprópria diverge, e a integral imprópria de ${f}$ no intervalo ${(-\infty,+\infty)}$ é

$\displaystyle \int_{-\infty}^{+\infty}f(x)\,\mathrm{d}x = \int_{-\infty}^cf(x)\,\mathrm{d}x+ \int_c^{+\infty}f(x)\,\mathrm{d}x$

quando o limite existe, caso contrário dizemos que a integral imprópria diverge.

Por exemplo, para calcular ${\int_{-\infty}^{+\infty} \frac 1{1+x^2}\,\mathrm{d}x}$ tomamos ${c=0}$ na definição acima e

$\displaystyle \int_{-\infty}^{0} \frac 1{1+x^2}\,\mathrm{d}x= \lim_{a\rightarrow-\infty} \int_{a}^{0} \frac 1{1+x^2}\,\mathrm{d}x= \lim_{a\rightarrow-\infty} \mathrm{arctan}(x)\Big|_{a}^{0} = \lim_{a\rightarrow-\infty} -\mathrm{arctan}(a)= \frac{\pi}2$

$\displaystyle \int_0^{+\infty} \frac 1{1+x^2}\,\mathrm{d}x= \lim_{b\rightarrow+\infty} \int_{0}^{b} \frac 1{1+x^2}\,\mathrm{d}x= \lim_{b\rightarrow+\infty} \mathrm{arctan}(x)\Big|_{0}^{b} = \lim_{b\rightarrow+\infty} \mathrm{arctan}(b)= \frac{\pi}2$

logo

$\displaystyle \int_{-\infty}^{+\infty} \frac 1{1+x^2}\,\mathrm{d}x =\pi.$

Se ${f}$ é contínua em ${[a,b]}$ exceto por uma descontinuidade infinita em ${b}$ então a integral imprópria de ${f}$ em ${[a,b]}$ nesse caso é

$\displaystyle \int_a^b f(x)\,\mathrm{d}x = \lim_{t\rightarrow b^-} \int_a^t f(x)\,\mathrm{d}x$

e caso haja uma descontinuidade infinita em ${a}$ então a integral imprópria de ${f}$ em ${[a,b]}$ nesse caso é

$\displaystyle \int_a^b f(x)\,\mathrm{d}x = \lim_{t\rightarrow a^+} \int_t^b f(x)\,\mathrm{d}x.$

Caso o limite não exista então dizemos que a integral imprópria diverge. Finalmente, se a descontinuidade infinita for em ${c\in [a,b]}$ então

$\displaystyle \int_a^b f(x)\,\mathrm{d}x = \int_a^c f(x)\,\mathrm{d}x+ \int_c^b f(x)\,\mathrm{d}x$

e dizemos que a integral diverge caso alguma das parcelas divirja.

Por exemplo,

$\displaystyle \int_1^2 \frac 1{1-x} = \lim_{t\rightarrow 1^+} \int_t^2 \frac 1{1-x}\,\mathrm{d}x= \lim_{t\rightarrow 1^+} \left(-\log |1-x| \Big|_t^2 \right)= -\infty$

portanto essa integral diverge.

Por exemplo

$\displaystyle \int_0^{+\infty} \frac 1{\sqrt{x}(x+1)}\,\mathrm{d}x = \int_0^1\frac 1{\sqrt{x}(x+1)}\,\mathrm{d}x + \int_1^{+\infty} \frac 1{\sqrt{x}(x+1)}\,\mathrm{d}x.$

Uma primitiva da função é ${2 \mathrm{arctan}\sqrt x +k}$ que pode ser determinada por substituição ${x=u^2}$ . Assim,

$\displaystyle \int_0^1\frac 1{\sqrt{x}(x+1)}\,\mathrm{d}x = \lim_{t\rightarrow 0^+}\left( 2\mathrm{arctan}\sqrt x\Big|_t^1 \right)= \frac \pi 2$

$\displaystyle \int_1^{+\infty}\frac 1{\sqrt{x}(x+1)}\,\mathrm{d}x = \lim_{t\rightarrow +\infty} \left(2\mathrm{arctan}\sqrt x\Big|^t_1\right) = \frac \pi 2.$

— Exemplo: Movimento retilíneo —

Sabemos que um corpo que se move em linha reta tem sua posição, velocidade e aceleração dados por ${s(t)}$ , ${v(t)}$ e ${a(t)}$ , respectivamente, de modo que

$\displaystyle v(t) = s'(t) \textrm{ e } a(t) = v'(t).$

Ademais, vimos no exemplo 69 que ${v}$ é uma primitiva de ${a}$

$\displaystyle v(t) = \int a(t)\,\mathrm{d}t$

e que ${v(t)}$ fica completamente determinada se conhecemos, por exemplo, ${v(0)}$ ; também, a partir daí, obtemos

$\displaystyle s(t) = \int v(t)\,\mathrm{d}t$

e que ${s(t)}$ fica completamente determinada se conhecemos, por exemplo, ${s(0)}$ .

O deslocamento de um corpo ao longo de intervalo de tempo ${[t_0,t_1]}$ é ${s(t_1)-s(t_0)}$ , ou seja, é dado por

$\displaystyle \int_{t_0}^{t_1} v(t) \, \mathrm{d}t \ \ \ \ \ (34)$

no entanto a distância percorrida ao longo desse intervalo é dada por

$\displaystyle \int_{t_0}^{t_1} |v(t)| \, \mathrm{d}t$

pois desconsideramos o sentido do deslocamento.

Notemos que se o movimento é uniformemente acelerado, isto é ${a(t)=a}$ constante, então

$\displaystyle v(t) = \int a(t)\,\mathrm{d}t = at + k$

e se ${v(0) = v_0}$ então ${k = v_0}$ e

$\displaystyle v(t) = at + v_0$

e a posição é

$\displaystyle s(t) = \int v(t)\,\mathrm{d}t = \int \big( at + v_0 \big)\,\mathrm{d}t= \frac {at}2 + v_0 t +k$

e se ${s(0)=s_0}$ então ${k=s_0}$ e

$\displaystyle s(t) =\frac {at}2 + v_0 t + s_0$

como é conhecido de todo estudante do ensino médio.

Ideia da prova do Teorema 18 Se ${f}$ é contínua então em cada subintervalo ${[x_{i},x_{i+1}]}$ a função é contínua, portanto, admite ponto de máximo ${M_i}$ e ponto de mínimo ${m_i}$ , pelo teorema de Weierstrass. Assim,

$\displaystyle \underbrace{\sum_{i=1}^n f(m_i)\Delta x_i}_{\underline{S_n}}\leq \underbrace{\sum_{i=1}^n f(\xi_i)\Delta x_i}_{S_n}\leq \underbrace{\sum_{i=1}^n f(M_i)\Delta x_i}_{\overline{S_n}},$

para quaisquer escolhas de ${x_i}$ e ${\xi_i}$ .

A diferença entre os limitantes inferior e superior é

$\displaystyle 0\leq \sum_{i=1}^n f(M_i)\Delta x_i - \sum_{i=1}^n f(m_i)\Delta x_i = \sum_{i=1}^n [f(M_i)-f(m_i)]\Delta x_i$

e da continuidade podemos garantir ${f(M_i)-f(m_i) < \varepsilon}$ se os ${\Delta x_i}$ ‘s forem suficientemente pequenos, portanto

$\displaystyle 0\leq \overline{S_n} - \underline{S_n} \leq \varepsilon(b-a) \ \ \ \ \ (32)$

consequentemente, no limite, a diferença ${\overline{S_n} - \underline{S_n} }$ é zero. Com isso, basta mostrar quer ${\overline{S_n}}$ converge pois ${\lim \overline{S_n} = \lim S_n = \lim \underline{S_n}.}$

Dadas as somas ${\overline{S_n}}$ e ${\overline{S_m}}$ consideremos uma soma ${\overline{S_\ell}}$ definida pelas escolhas dos ${x_i}$ das somas anteriores tomados conjuntamente. Então

$\displaystyle \underline{S_n} \leq \overline{S_\ell} \leq \overline{S_n} \quad \textrm{ e }\quad \underline{S_m}\leq \overline{S_\ell} \leq \overline{S_m} \ \ \ \ \ (33)$

Vamos justificar a primeira desigualdade, a segunda tem justificativa análoga. O ${i}$ -ésimo intervalo da soma ${{S_n}}$ abrange um ou mais subintervalos da soma ${{S_\ell}}$ , os termos dessa soma correspondentes a tais subintervalos tem ${(1)}$ variação menor que o ${\Delta x_i}$ do ${i}$ -ésimo intervalo da soma ${{S_n}}$ com soma dessas variações sendo ${\Delta x_i}$ , e ${(2)}$ valor da função entre ${f(m_i)}$ e ${f(M_i)}$ . Portanto, essa parcela de termos da soma ${\overline{S_\ell}}$ tem valor entre ${f(m_i)\Delta x_i}$ e ${f(M_i)\Delta x_i}$ .

De (33)

$\displaystyle 0 \leq \overline{S_\ell} - \underline{S_n} \leq \overline{S_n} -\underline{S_n}\quad \textrm{ e }\quad 0\leq \overline{S_\ell} -\underline{S_m}\leq \overline{S_m}-\underline{S_m}$

e de (32)

$\displaystyle \overline{S_n} -\underline{S_n} < \varepsilon(b-a) \quad \textrm{ e }\quad \overline{S_m}-\underline{S_m}< \varepsilon(b-a)$

se os subintervalos são suficientemente pequenos. Com isso

$\displaystyle | \overline{S_n} - \overline{S_m}| = | \overline{S_n} - \overline{S_\ell} - \overline{S_m} + \overline{S_\ell}| \leq | \overline{S_n} - \overline{S_\ell}|+ | \overline{S_\ell} - \overline{S_\ell}| < 2\varepsilon (b-a).$

Como ${\varepsilon >0}$ pode ser feito arbitrariamente pequeno, pelo critério de convergência de Cauchy a sequência ${\overline{S_n}}$ converge. ${\Box}$

Notas de aula

Jair Donadelli

bc0402 Integral

Deixe um comentário Cancelar resposta

Compartilhe isso:

Relacionado

Deixe um comentário Cancelar resposta